|
|
| Строка 1: |
Строка 1: |
| − | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;"
| |
| − | |+
| |
| − | |-align="center"
| |
| − | |'''НЕТ ВОЙНЕ'''
| |
| − | |-style="font-size: 16px;"
| |
| − | |
| |
| − | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян.
| |
| − |
| |
| − | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием.
| |
| − |
| |
| − | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей.
| |
| − |
| |
| − | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить.
| |
| − |
| |
| − | ''Антивоенный комитет России''
| |
| − | |-style="font-size: 16px;"
| |
| − | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.
| |
| − | |-style="font-size: 16px;"
| |
| − | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки].
| |
| − | |}
| |
| − |
| |
| | {{Определение | | {{Определение |
| | |definition= | | |definition= |
| Определение: |
| Производящие функции нескольких переменных (англ. multivariable generating function) — обычные производящие функции, зависящие более, чем от одной переменной. Очень часто применяются функции от двух переменных (далее они и будут рассматриваться), которые в общем случае принимают вид:
[math]G(x, y) = \sum\limits_{n, k \geqslant 0} g_{n, k} x^n y^k[/math]. |
Рассмотрим несколько примеров :
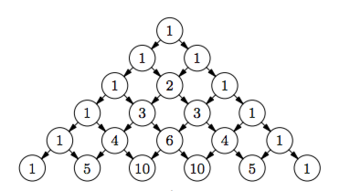
Треугольник Паскаля
| Определение: |
| Треугольник Паскаля (англ. Pascal's triangle) — бесконечная таблица биномиальных коэффициентов[1], имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. |
Элементы треугольника (рис.[math]1[/math]) перечисляют пути, идущие из его вершины в соответствующую клетку. Пути имеют вид ломаных, составленных из векторов единичной длины двух видов: идущих вправо-вниз и идущих влево-вниз.
Производящая функция может быть сопоставлена треугольнику Паскаля несколькими способами. Например, можно рассмотреть производящую функцию
[math]\displaystyle\sum\limits_{n,k = 0}^{\infty} c_{n,k} x^k y^n = \sum\limits_{n,k = 0}^{\infty} \binom{n}{k} x^k y^n = \sum\limits_{n = 0}^{\infty}[/math][math]\Big(\sum\limits_{k = 0}^{n} \binom{n}{k} x^k\Big) y^n = \displaystyle\sum\limits_{n = 0}^{\infty} (1 + x)^n y^n = \dfrac{1}{1 - y - xy}[/math]
Второй способ соответствует нумерации элементов треугольника числом отрезков каждого типа на путях, ведущих в соответствующую точку (рис.[math]2[/math]) [math]C_{n,m} = c_{n+m, n} = \dbinom{n+m}{m}[/math]. Тогда производящая функция будет иметь вид
[math]\displaystyle\sum\limits_{n,m = 0}^{\infty} C_{n, m} x^n y^m = \sum\limits_{n,m = 0}^{\infty} \binom{n+m}{m} x^n y^m = \sum\limits_{k = 0}^{\infty}[/math][math] \Big(\sum\limits_{n + m = k} \binom{n+m}{n}
x^n y^m \Big)=\displaystyle\sum\limits_{k = 0}^{\infty} (x + y)^k = \dfrac{1}{1 -x - y}[/math]
Также существует еще один способ: сопоставить треугольнику Паскаля экспоненциальную производящую функцию. Экспоненциальная производящая функция отличается от обычной тем, что в качестве коэффициентов степенного ряда берутся не элементы последовательности [math]a_n[/math], а числа [math]\dfrac{a_n}{n!}[/math].
Экспоненциальные производящие функции
Зафиксируем произвольную последовательность [math]\{ \alpha_n \}[/math]. Каждой последовательности [math]\{ \alpha_n \}[/math] мы можем сопоставить производящую функцию
[math]\{ \alpha_n \} \mapsto \sum\limits_{n = 0}^{\infty} a_n \alpha_n s^n[/math]
определяемую последовательностью [math]\{ \alpha_n \}[/math]. Если в последовательности [math]\{ \alpha_n \}[/math] отсутствуют нулевые элементы, то такое сопоставление взаимно однозначно. До сих пор мы пользовались обычными производящими функциями, отвечающими последовательности [math]\{ \alpha_n \} \equiv 1[/math]. В зависимости от преследуемых целей могут принести и другие последовательности.
| Определение: |
| Производящие экспоненциальные функции (англ. exponential generating function) — функции, соответствующие последовательности [math]\{ \alpha_n \} = \dfrac{1}{n!}[/math]. |
| Определение: |
| Экспоненциальные производящие функции для целочисленных последовательностей называют функциями Гурвица (англ. Hurwitz function). |
Чем отличаются экспоненциальные производящие функции от обычных? Посмотрим на поведение экспоненциальных производящих функций при выполнении операции над ними. Сумма ведет себя обычным образом:
[math]\displaystyle\sum\limits_{n = 0}^{\infty} \dfrac{a_n}{n!}s^n + \sum\limits_{n = 0}^{\infty} \dfrac{b_n}{n!}s^n = \sum\limits_{n = 0}^{\infty} \dfrac{(a_n + b_n)}{n!} s^n[/math]
а с произведением по-другому:
[math]\bigg(\dfrac{a_0}{0!} + \dfrac{a_1}{1!}s + \dfrac{a_2}{2!}s^2 + \ldots\bigg)\bigg(\dfrac{b_0}{0!} + \dfrac{b_1}{1!}s + \dfrac{b_2}{2!}s^2 + \ldots\bigg) = \dfrac{a_0}{0!} \dfrac{b_0}{0!} + \bigg(\dfrac{a_0}{0!} \dfrac{b_1}{1!} + \dfrac{a_1}{1!} \dfrac{b_0}{0!}\bigg)s + \bigg(\dfrac{a_0}{0!} \dfrac{b_2}{2!} + \dfrac{a_1}{1!} \dfrac{b_1}{1!} + \dfrac{a_2}{2!} \dfrac{b_0}{0!}\bigg)s^2 + \ldots[/math]
Коэффициенты [math]\dfrac{c_n}{n!}[/math] произведения вычисляются по формуле
[math]c_n = \begin{pmatrix} n \\ 0 \end{pmatrix} a_0 b_n + \begin{pmatrix} n \\ 1 \end{pmatrix} a_1 b_{n - 1} + \ldots + \begin{pmatrix} n \\ n \end{pmatrix} a_n b_0[/math]
Еще одно существенное отличие экспоненциальных производящих функций от обычных наблюдается при взятии производных и при интегрировании. Дифференцирование или интегрирование экспоненциальной производящей функции приводит к сдвигу последовательности ее коэффициентов без изменения их величины:
[math]\bigg( \dfrac{a_0}{0!} + \dfrac{a_1}{1!}s + \dfrac{a_2}{2!}s^2 + \ldots \bigg)^{'} = \dfrac{a_1}{0!} + \dfrac{a_2}{1!}s + \dfrac{a_3}{2!}s^2 + \ldots [/math]
[math]\displaystyle\int \bigg(\dfrac{a_0}{0!} + \dfrac{a_1}{1!}s + \dfrac{a_2}{2!}s^2 + \ldots \bigg) = \dfrac{a_0}{1!}s + \dfrac{a_1}{2!}s^2 + \dfrac{a_2}{3!}s^3 + \dfrac{a_3}{4!}s^4 + \ldots [/math]
Обычная производящая функция [math]A(s) = a_0 + a_1s + a_2s^2 + \ldots[/math] выражается через экспоненциальную [math]B(t) = \dfrac{a_0}{0!} + \dfrac{a_1}{1!}t + \dfrac{a_2}{2!}t^2 + \ldots [/math] по формуле
[math]A(s) = \int\limits_{0}^{\infty} e^{-t} B(st) dt[/math]
Действительно,
[math]k! = \int\limits_{0}^{\infty} e^{-t}t^kdt[/math]
Теперь можно выписать экспоненциальную производящую функцию для треугольника Паскаля:
[math]\displaystyle\sum\limits_{n, m = 0}^{\infty} \dfrac{1}{(n + m)!} \dbinom{n+m}{m} x^n y^m = \sum\limits_{n = 0}^{\infty} \dfrac{(x + y)^n}{n!} = e^{x + y}[/math]
Многочлены Бернулли
Для начала введём операцию усреднения, положив
[math]A(f(x)) = \int\limits_{x}^{x+1}f(t)dt[/math].
Нетрудно заметить, что эта операция переводит многочлены в многочлены: она линейна, т.е. [math]A(a_1f_1 + a_2f_2) = a_1A(f_1) + a_2A(f_2)[/math] для любых постоянных [math]a_1, a_2[/math] и любых многочленов [math]f_1,
f_2[/math], а ее значение на мономе[2] [math]x^n[/math] равно
[math]A(x^n) = ((x + 1)^{n+1} - x^{n+1}) / (n+1) = x^n + \ldots[/math],
где многоточие обозначает слагаемые, степени которых меньше [math]n[/math]. Последняя формула показывает также, что преобразование [math]A[/math] переводит пространство многочленов степени не выше [math]n[/math] в себя, а значит, является линейным оператором в этом пространстве. Этот оператор обратим. Действительно, любой многочлен степени не выше [math]n-1[/math] может быть получен в результате усреднения многочлена такой же степени, и, используя последнюю формулу, мы заключаем, что и любой многочлен степени не выше [math]n[/math] является результатом усреднения некоторого многочлена степени не выше [math]n[/math]. Отметим, что при усреднении степень многочлена сохраняется.
| Определение: |
| Многочленом Бернулли (англ. Bernoulli polynomial) степени [math]n[/math] называется многочлен [math]B_n(x)[/math], результатом усреднения которого служит моном [math]x^n[/math], т.е. [math]B_n(x) = A^{-1}(x^n)[/math]. |
Первые многочлены Бернулли нетрудно сосчитать:
[math]B_0(x) = 1[/math]
[math]B_1(x) = x - \dfrac{1}{2}[/math]
[math]B_2(x) = x^2 -x + \dfrac{1}{6}[/math]
[math]B_3(x) = x^3 - \dfrac{3}{2}x^2 + \dfrac{1}{2}x[/math]
[math]B_4(x) = x^4 - 2x^3 + x^2 - \dfrac{1}{30}[/math]
[math]B_5(x) = x^5 - \dfrac{5}{2}x^4 + \dfrac{5}{3}x^3 - \dfrac{1}{6}x[/math]
[math]B_6(x) = x^6 - 3x^5 + \dfrac{5}{2}x^4 - \dfrac{1}{2}x^2 + \dfrac{1}{42}[/math]
| Теорема (Экспоненциальная производящая функция для многочленов Бернулли): |
Экспоненциальная производящая функция для многочленов Бернулли имеет вид:
[math]\mathcal{B}(x, s) = \displaystyle\sum\limits_{n=0}^{\infty}B_n(x)\dfrac{s^n}{n!} = \dfrac{s}{e^s - 1}e^{sx}[/math]. |
| Доказательство: |
| [math]\triangleright[/math] |
|
Для доказательства теоремы достаточно применить операцию усреднения к левой и правой частям равенства. С одной стороны, мы имеем:
[math]A(B(x, s)) = \displaystyle\sum\limits_{n=0}^{\infty}A(B_n(x))\dfrac{s^n}{n!} = \sum\limits_{n=0}^{\infty}x^n\dfrac{s^n}{n!} = e^{xs}[/math].
С другой стороны, имеем:
[math]A(\dfrac{s}{e^s - 1}e^{sx}) = \dfrac{s}{e^s-1}A(e^{sx}) = \dfrac{s}{e^s-1}\dfrac{1}{s}(e^{s(x+1)} - e^{sx}) = e^{sx}[/math],
и теорема доказана. |
| [math]\triangleleft[/math] |
Определим теперь числа Бернулли[3] как значения многочленов Бернулли в нуле. Вот начало последовательности чисел Бернулли:
[math]1, -\dfrac{1}{2}, 0, \dfrac{1}{6}, -\dfrac{1}{30}, \dfrac{1}{42}, 0, -\dfrac{1}{30}, \dfrac{5}{66}, 0, -\dfrac{691}{2730}, 0, \ldots [/math]
Доказанная теорема позволяет нам легко выписать экспоненциальную производящую функцию для чисел Бернулли. Для этого достаточно подставить в экспоненциальную производящую функцию для многочленов Бернулли значение [math]x = 0[/math]:
[math]\displaystyle\sum\limits_{n=0} B_n\dfrac{s^n}{n!} = \dfrac{s}{e^s - 1}[/math].
См. также
Примечания
Источники информации
- Ландо С. К., Лекции о производящих функциях. — 3-е изд., испр. — М.: МЦНМО, 2007. — 57с. ISBN 978-5-94057-042-4