Алгоритм для причинно-согласованного порядка — различия между версиями
Yeputons (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 4 промежуточные версии 2 участников) | |||
| Строка 1: | Строка 1: | ||
| + | [[Категория: Параллельное программирование]] | ||
Этот алгоритм берёт систему с асинхронным порядком и начинает гарантировать в ней [[Иерархия порядков сообщений#Причинно-согласованный порядок|причинно-согласованный порядок]]. | Этот алгоритм берёт систему с асинхронным порядком и начинает гарантировать в ней [[Иерархия порядков сообщений#Причинно-согласованный порядок|причинно-согласованный порядок]]. | ||
| Строка 16: | Строка 17: | ||
Как и в алгоритме для FIFO, тут очередь принятых, но не обработанных сообщений может раздуваться бесконечно. | Как и в алгоритме для FIFO, тут очередь принятых, но не обработанных сообщений может раздуваться бесконечно. | ||
| − | Но тут нам сложнее обрабатывать сообщения в очереди: в FIFO это было независимо по процессам и можно было сложить их в очередь с приоритетом, а тут сообщение от одного процесса может вызвать лавину сообщений от остальных, надо перебирать. | + | Но тут нам сложнее обрабатывать сообщения в очереди: в FIFO это было независимо по процессам и можно было сложить их в очередь с приоритетом, а тут сообщение от одного процесса может вызвать лавину сообщений |
| + | от остальных, надо перебирать. | ||
| − | Псевдокод | + | == Псевдокод == |
'''var''' | '''var''' | ||
M:array[l..N, 1..N] of integer initially 0; | M:array[l..N, 1..N] of integer initially 0; | ||
| Строка 27: | Строка 29: | ||
'''enabled if''' W[j,i] = M [j,i] + 1 <tex>\land</tex> <tex> \forall k \neq j</tex> <tex>M[k, i] \geqslant W[k, i]</tex> | '''enabled if''' W[j,i] = M [j,i] + 1 <tex>\land</tex> <tex> \forall k \neq j</tex> <tex>M[k, i] \geqslant W[k, i]</tex> | ||
M := max(M, W) | M := max(M, W) | ||
| + | |||
| + | == Пример == | ||
| + | Пусть есть три процесса: $P$, $Q$, $R$ (пронумерованных так же) и они отправили друг другу сообщения. Процесс $R$ только что получил сообщение: | ||
| + | |||
| + | [[Файл:distributed-order-cc-algo-1.png|400px]] | ||
| + | |||
| + | Так как у процесса $R$ матрица $M$ нулевая, а $W_{23}=1$, то FIFO-порядок не нарушен. Однако в столбце 3 (сообщения, посланные процессу $R$) в строчке 1 (от процесса $P$) есть единица, что больше, чем ноль. То есть $P$ послал сообщение $R$, $Q$ про это знает, но $R$ ещё это сообщение не получил. Тогда надо ждать сообщения, матрицу пока не обновляем. | ||
| + | |||
| + | [[Файл:distributed-order-cc-algo-2.png|400px]] | ||
| + | |||
| + | Тут как раз получили это сообщение. Столбец 3 совпадает, а в строчке 1 у нас на единицу больше, т.е. FIFO между $P$ и $Q$ не нарушен. Можно обработать сообщение и обновить матрицу $M$. Теперь можно обработать то сообщение, которое было получено первым: | ||
| + | |||
| + | [[Файл:distributed-order-cc-algo-3.png|400px]] | ||
Текущая версия на 19:19, 4 сентября 2022
Этот алгоритм берёт систему с асинхронным порядком и начинает гарантировать в ней причинно-согласованный порядок.
Идея похожа на Алгоритм для FIFO порядка: прикрепить к каждому сообщению "номер" и обрабатывать только сообщения со следующим ожидаемым номером, а остальные складывать в очередь. Нам надо не только знать следующее ожидаемое сообщение от каждого процесса, но и
Используется что-то вроде матричных часов, но не совсем они (см. раздел 7.7 на странице 125 и раздел 12.2 на странице 193 в Gaarg).
Каждый процесс поддерживает счётчик-матрицу: $M_{i,j}$ — количество сообщений, отправленных процессом $i$ процессом $j$ (по мнению хранящего матрицу). Эта матрица отправляется с каждым сообщением, перед посылкой мы увеличиваем соответствующее число в ней на единицу.
Когда процесс $P_i$ с матрицей $M$ получил от $P_j$ сообщение с матрицей $W$, то:
- Если $W_{ji}=M_{ji}+1$, то это ожидаемое сообщение с точки зрения FIFO-порядка между $P_i$ и $P_j$. Иначе надо отложить в очередь.
- Если существует $k \neq j$ такое, что $W_{ki} > M_{ki}$, то это значит, что процесс $k$ отправил нам сообщение, процесс $j$ про это в курсе, а мы ещё его не получили. Тогда для причинно-согласованности надо сначала подождать это сообщение, а потом обрабатывать сообщение от $P_j$.
- Если же такого $k$ не существует, то уже можно обработать сообщение и ничего не нарушится (строго не доказывали).
- Непосредственно перед тем, как обработать сообщение, надо обновить свою матрицу $M$, взяв покомпонентный максимум всех значений.
Как и в алгоритме для FIFO, тут очередь принятых, но не обработанных сообщений может раздуваться бесконечно. Но тут нам сложнее обрабатывать сообщения в очереди: в FIFO это было независимо по процессам и можно было сложить их в очередь с приоритетом, а тут сообщение от одного процесса может вызвать лавину сообщений от остальных, надо перебирать.
Псевдокод
var
M:array[l..N, 1..N] of integer initially 0;
To send a message to :
M [i,j] := M[i,j] + 1;
send M as part of the message;
To receive a message with matrix W from Pj:
enabled if W[j,i] = M [j,i] + 1
M := max(M, W)
Пример
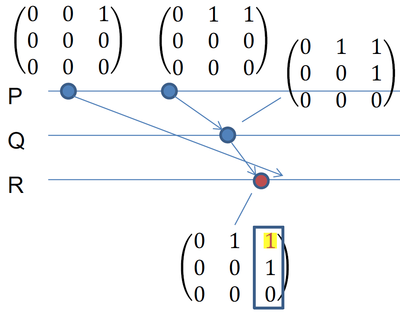
Пусть есть три процесса: $P$, $Q$, $R$ (пронумерованных так же) и они отправили друг другу сообщения. Процесс $R$ только что получил сообщение:
Так как у процесса $R$ матрица $M$ нулевая, а $W_{23}=1$, то FIFO-порядок не нарушен. Однако в столбце 3 (сообщения, посланные процессу $R$) в строчке 1 (от процесса $P$) есть единица, что больше, чем ноль. То есть $P$ послал сообщение $R$, $Q$ про это знает, но $R$ ещё это сообщение не получил. Тогда надо ждать сообщения, матрицу пока не обновляем.
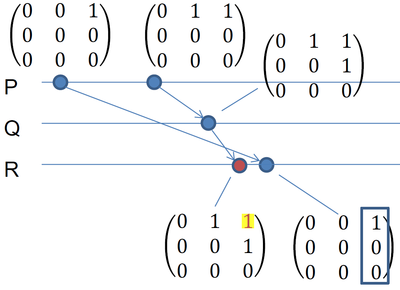
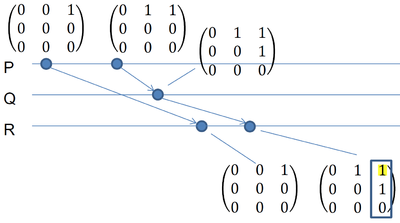
Тут как раз получили это сообщение. Столбец 3 совпадает, а в строчке 1 у нас на единицу больше, т.е. FIFO между $P$ и $Q$ не нарушен. Можно обработать сообщение и обновить матрицу $M$. Теперь можно обработать то сообщение, которое было получено первым: