Алгоритм вырезания соцветий — различия между версиями
Kot (обсуждение | вклад) (→Алгоритм нахождения паросочетания в недвудольном графе) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 34 промежуточные версии 9 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
== Паросочетание в недвудольном графе== | == Паросочетание в недвудольном графе== | ||
| − | {{ | + | Рассмотрим неориентированный невзвешенный [[Основные определения теории графов|граф]] <tex> G =\langle V, E \rangle </tex>, где <tex>V </tex> {{---}} множество [[Основные определения теории графов| вершин]], <tex>E </tex> {{---}} множество [[Основные определения теории графов|рёбер]]. Требуется найти в нём максимальное паросочетание. |
| − | | | + | |
| − | + | Приведём пример, на котором [[Алгоритм Куна для поиска максимального паросочетания|алгоритм Куна]] работать не будет. Рассмотрим граф <tex>G</tex> с множеством вершин <tex>V={1,2,3,4} </tex>, и множеством рёбер {{---}}<tex>E={\langle 1,2 \rangle, \langle 2, 3 \rangle, \langle 3, 1 \rangle, \langle 2, 4 \rangle}</tex> и пусть ребро <tex>\langle 2, 3\rangle</tex> взято в паросочетание. Тогда при запуске из вершины <tex>1</tex>, если обход пойдёт сначала в вершину <tex>2</tex>, то он зайдёт в тупик в вершине <tex>3</tex>, вместо того чтобы найти увеличивающую цепь <tex>1-3-2-4</tex>. Как видно на этом примере, основная проблема заключается в том, что при попадании в цикл нечётной длины, обход может пойти по циклу в неправильном направлении. | |
| − | |||
| − | |||
| − | |||
== Теорема Эдмондса == | == Теорема Эдмондса == | ||
| Строка 13: | Строка 9: | ||
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
| − | Пусть в | + | Пусть даны граф <tex>G</tex>, паросочетание <tex>M</tex> в <tex>G</tex> и цикл <tex>Z</tex> длины <tex>2k+1</tex>, содержащий <tex>k</tex> рёбер паросочетания <tex>M</tex> и вершинно непересекающийся с остальными рёбрами из <tex>M</tex>. Построим новый граф <tex>G'</tex> из графа <tex>G</tex>, сжимая цикл <tex>Z</tex> до единичной вершины, при этом все ребра, инцидентные вершинам этого цикла, становятся инцидентными вершине в новом графе. Тогда паросочетание <tex>M -E(Z)</tex>, где <tex>E(z)</tex> {{---}} ребра, инцидентные циклу, является наибольшим в <tex>G'</tex> тогда и только тогда, когда М {{---}} наибольшее паросочетание в <tex>G</tex> |
| − | Тогда в <tex>G</tex> | ||
|proof= | |proof= | ||
| − | + | Предположим, что <tex>M</tex> не является наибольшим паросочетанием в <tex>G</tex>, тогда в силу [[Теорема о максимальном паросочетании и дополняющих_цепях|теоремы о максимальном паросочетании и дополняющих цепях]] существует увеличивающая относительно <tex>M</tex> цепь <tex>P</tex>. Если <tex>P</tex> не пересекается с <tex>Z</tex>, то цепь является увеличивающей относительно <tex>M'</tex> и в графе <tex>G'</tex>, а значит, <tex>M'</tex> не может быть наибольшим паросочетанием. Поэтому предположим, что цепь <tex>P</tex> пересекается с <tex>Z</tex>. Заметим, что хотя бы одна концевая вершина цепи <tex>P</tex> не лежит на <tex>Z</tex>, обозначим её через <tex>u</tex>. Тогда пройдём по цепи <tex>P</tex>, начиная с <tex>u</tex> до первой встречной вершины на <tex>Z</tex>, обозначим её через <tex>v</tex>. Тогда, при сжатии цикла <tex>Z</tex>, участок <tex>P[u,v]</tex> отобразится на увеличивающую цепь относительно <tex>M'</tex>, то есть <tex>M'</tex> не является максимальным паросочетанием, что противоречит нашему предположению. | |
| − | Заметим, что | + | |
| + | Теперь допустим, что <tex>M'</tex> не является наибольшим паросочетанием в графе <tex>G'</tex>. Обозначим через <tex>N'</tex> паросочетание в <tex>G'</tex>, мощности большей, чем <tex>M'</tex>. Восстановим граф <tex>G</tex>, тогда <tex>N'</tex> будет соответствовать некоторому паросочетанию в <tex>G</tex>, покрывающему не более одной вершины в <tex>Z</tex>. Следовательно паросочетание <tex>N'</tex> можно увеличить, используя <tex>k</tex> рёбер цикла <tex>Z</tex>, и получить паросочетание <tex>N</tex>, размера <tex>|N| = |N'|+k > |M'|+k = |M|</tex>, то есть <tex>M</tex> не является наибольшим паросочетанием в <tex>G</tex>, приходим к противоречию. Таким образом теорема доказана. | ||
| + | }} | ||
| + | |||
| + | Для простоты описания алгоритма введём некоторые определения. | ||
| + | {{Определение | ||
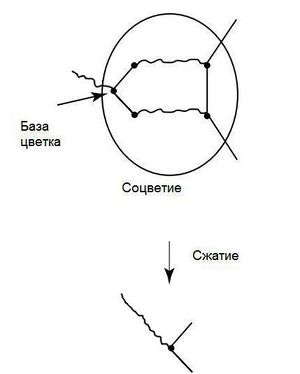
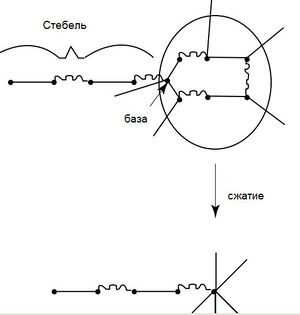
| + | |definition= Будем называть '''соцветием''' <tex>B</tex> графа <tex>G</tex> его цикл нечётной длины. | ||
| − | <tex> | + | '''Cжатием соцветия''' назовём граф <tex>G'</tex>, полученный из <tex>G</tex> сжатием всего нечётного цикла в одну псевдо-вершину. Все рёбра, инцидентные вершинам этого цикла, становятся инцидентными псевдо-вершине в новом графе. |
| − | + | '''База соцветия''' - вершина соцветия, в которую входит ребро не из данного соцветия. | |
| − | + | }} | |
| − | + | [[Файл:blossom1.jpg|300px|Рис. 1]] | |
| + | [[Файл:blossom2.jpg|300px|Рис. 2]] | ||
| − | + | ==Алгоритм вырезания соцветий== | |
| + | Опишем алгоритм, позволяющий находить максимальное паросочетание для произвольного графа <tex>G</tex>. Из теоремы Эдмондса понятно, что необходимо рассматривать паросочетание в сжатом графе, где его можно найти, к примеру, при помощи алгоритма [[Алгоритм Куна для поиска максимального паросочетания|Куна]], а после восстанавливать паросочетание в исходном графе. | ||
| − | + | Основную сложность представляют операции сжатия и восстановления цветков. Чтобы эффективно это делать, для каждой вершины необходимо хранить указатель на базу цветка, которому она принадлежит, или на себя в противном случае. Предположим, что для поиска паросочетаний в сжатом графе, мы используем обход в ширину. Тогда на каждой итерации алгоритма будет строиться дерево обхода в ширину, причём путь в нём до любой вершины будет являться чередующимся путём, начинающимся с корня этого дерева. Будем класть в очередь только те вершины, расстояние от корня до которых в дереве путей чётно. Также для каждой вершины, расстояние до которой нечётно, в массиве предков <tex>p[]</tex> необходимо хранить её предка {{---}} чётную вершину. Заметим, что если в процессе обхода в ширину мы из текущей вершины <tex>v</tex> приходим в такую вершину <tex>u</tex>, что она является корнем или принадлежит паросочетанию и дереву путей, то обе эти вершины принадлежат некоторому цветку. Действительно, при выполнении этих условий эти вершины являются чётными вершинами, следовательно расстояние от них до их наименьшего общего предка имеет одну чётность. Найдём наименьшего общего предка <tex>lca(u,v)</tex> вершин <tex>u</tex>, <tex>v</tex>, который является базой цветка. Для нахождения самого цикла необходимо пройтись от вершин <tex>u</tex>, <tex>v</tex> до базы цветка. В явном виде цветок сжимать не будем, просто положим в очередь обхода в ширину все вершины, принадлежащие цветку. Также для всех чётных вершин (за исключением базы) назначим предком соседнюю вершину в цикле, а для вершин <tex>u</tex> и <tex>v</tex> назначим предками друг друга. Это позволит корректно восстановить цветок в случае, когда при восстановлении увеличивающего пути мы зайдем в нечётную вершину цикла. | |
| − | + | == Оценка сложности == | |
| − | |||
| − | + | Всего имеется <tex>V</tex> итераций, на каждой из которых выполняется обход в ширину за <tex>O(E)</tex>, кроме того, могут происходить операции сжатия цветков — их может быть <tex>O(V)</tex>. Сжатие соцветий работает за <tex>O(V)</tex>, то есть общая асимптотика алгоритма составит <tex>O(V(E + V^2)) = O(V^3)</tex>. | |
| − | + | ==Литература== | |
| + | *''Ловас, Пламмер'' '''Прикладные задачи теории графов. Теория паросочетаний в математике и физике''' | ||
| + | *[http://e-maxx.ru/algo/matching_edmonds Алгоритм Эдмондса нахождения наибольшего паросочетания в произвольных графах] | ||
| − | + | [[Категория: Алгоритмы и структуры данных]] | |
| − | + | [[Категория: Задача о паросочетании]] | |
Текущая версия на 19:21, 4 сентября 2022
Содержание
Паросочетание в недвудольном графе
Рассмотрим неориентированный невзвешенный граф , где — множество вершин, — множество рёбер. Требуется найти в нём максимальное паросочетание.
Приведём пример, на котором алгоритм Куна работать не будет. Рассмотрим граф с множеством вершин , и множеством рёбер — и пусть ребро взято в паросочетание. Тогда при запуске из вершины , если обход пойдёт сначала в вершину , то он зайдёт в тупик в вершине , вместо того чтобы найти увеличивающую цепь . Как видно на этом примере, основная проблема заключается в том, что при попадании в цикл нечётной длины, обход может пойти по циклу в неправильном направлении.
Теорема Эдмондса
| Теорема: |
Пусть даны граф , паросочетание в и цикл длины , содержащий рёбер паросочетания и вершинно непересекающийся с остальными рёбрами из . Построим новый граф из графа , сжимая цикл до единичной вершины, при этом все ребра, инцидентные вершинам этого цикла, становятся инцидентными вершине в новом графе. Тогда паросочетание , где — ребра, инцидентные циклу, является наибольшим в тогда и только тогда, когда М — наибольшее паросочетание в |
| Доказательство: |
|
Предположим, что не является наибольшим паросочетанием в , тогда в силу теоремы о максимальном паросочетании и дополняющих цепях существует увеличивающая относительно цепь . Если не пересекается с , то цепь является увеличивающей относительно и в графе , а значит, не может быть наибольшим паросочетанием. Поэтому предположим, что цепь пересекается с . Заметим, что хотя бы одна концевая вершина цепи не лежит на , обозначим её через . Тогда пройдём по цепи , начиная с до первой встречной вершины на , обозначим её через . Тогда, при сжатии цикла , участок отобразится на увеличивающую цепь относительно , то есть не является максимальным паросочетанием, что противоречит нашему предположению. Теперь допустим, что не является наибольшим паросочетанием в графе . Обозначим через паросочетание в , мощности большей, чем . Восстановим граф , тогда будет соответствовать некоторому паросочетанию в , покрывающему не более одной вершины в . Следовательно паросочетание можно увеличить, используя рёбер цикла , и получить паросочетание , размера , то есть не является наибольшим паросочетанием в , приходим к противоречию. Таким образом теорема доказана. |
Для простоты описания алгоритма введём некоторые определения.
| Определение: |
| Будем называть соцветием графа его цикл нечётной длины.
Cжатием соцветия назовём граф , полученный из сжатием всего нечётного цикла в одну псевдо-вершину. Все рёбра, инцидентные вершинам этого цикла, становятся инцидентными псевдо-вершине в новом графе. База соцветия - вершина соцветия, в которую входит ребро не из данного соцветия. |
Алгоритм вырезания соцветий
Опишем алгоритм, позволяющий находить максимальное паросочетание для произвольного графа . Из теоремы Эдмондса понятно, что необходимо рассматривать паросочетание в сжатом графе, где его можно найти, к примеру, при помощи алгоритма Куна, а после восстанавливать паросочетание в исходном графе.
Основную сложность представляют операции сжатия и восстановления цветков. Чтобы эффективно это делать, для каждой вершины необходимо хранить указатель на базу цветка, которому она принадлежит, или на себя в противном случае. Предположим, что для поиска паросочетаний в сжатом графе, мы используем обход в ширину. Тогда на каждой итерации алгоритма будет строиться дерево обхода в ширину, причём путь в нём до любой вершины будет являться чередующимся путём, начинающимся с корня этого дерева. Будем класть в очередь только те вершины, расстояние от корня до которых в дереве путей чётно. Также для каждой вершины, расстояние до которой нечётно, в массиве предков необходимо хранить её предка — чётную вершину. Заметим, что если в процессе обхода в ширину мы из текущей вершины приходим в такую вершину , что она является корнем или принадлежит паросочетанию и дереву путей, то обе эти вершины принадлежат некоторому цветку. Действительно, при выполнении этих условий эти вершины являются чётными вершинами, следовательно расстояние от них до их наименьшего общего предка имеет одну чётность. Найдём наименьшего общего предка вершин , , который является базой цветка. Для нахождения самого цикла необходимо пройтись от вершин , до базы цветка. В явном виде цветок сжимать не будем, просто положим в очередь обхода в ширину все вершины, принадлежащие цветку. Также для всех чётных вершин (за исключением базы) назначим предком соседнюю вершину в цикле, а для вершин и назначим предками друг друга. Это позволит корректно восстановить цветок в случае, когда при восстановлении увеличивающего пути мы зайдем в нечётную вершину цикла.
Оценка сложности
Всего имеется итераций, на каждой из которых выполняется обход в ширину за , кроме того, могут происходить операции сжатия цветков — их может быть . Сжатие соцветий работает за , то есть общая асимптотика алгоритма составит .
Литература
- Ловас, Пламмер Прикладные задачи теории графов. Теория паросочетаний в математике и физике
- Алгоритм Эдмондса нахождения наибольшего паросочетания в произвольных графах