Алгоритм Фараха — различия между версиями
Slavian (обсуждение | вклад) (→Шаг 2: построение чётного дерева) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 23 промежуточные версии 5 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | '''Алгоритм Фараха''', разработанный в 1997 году американским ученым Мартином Фарах-Колтоном (Martin Farach-Colton) {{---}} алгоритм построения [[Сжатое суффиксное дерево|суффиксного дерева]] для заданной строки <tex>s</tex> длины <tex>N</tex>. Сам алгоритм выполняется за время <tex>O(N)</tex>, причём даже не требуется выполнение условия конечности алфавита. Такая эффективность достигается за счёт того, что строковые последовательности определяются на индексированном алфавите или, что эквивалентно, на целочисленном алфавите <tex>\Sigma = \{1, 2 \dots , k\}</tex>. При этом накладывается дополнительное условие, что <tex>k = O(N)</tex>. Такие алфавиты часто встречаются на практике. | |
| − | '''Алгоритм | + | Важно помнить, что алгоритм скорее теоретический, нежели практический, а основная его ценность заключается в том, что размер алфавита может быть произвольным. |
| − | Важно помнить, что алгоритм скорее теоретический, | ||
== Описание алгоритма == | == Описание алгоритма == | ||
| − | Идея алгоритма | + | Идея алгоритма состоит в том, что мы уменьшаем размер исходной строки, строим суффиксное дерево для неё рекурсивно, а потом получаем из построенного дерево для текущей строки. Для этого мы разбиваем символы исходной строки на пары и нумеруем их, а из полученных номеров составляем новую строку, которая уже в <tex>2</tex> раза короче. |
| − | Алгоритм | + | Алгоритм Фараха будет описан в виде пяти выполняемых шагов. Используем в качестве примера строку <tex>s = 121112212221</tex>, определенную на алфавите <tex>\Sigma = \{1, 2\} </tex> (в этом примере <tex>N = 12</tex>). |
=== Шаг 1: суффиксное дерево для сжатой строки=== | === Шаг 1: суффиксное дерево для сжатой строки=== | ||
| + | [[Файл:tree101232.png|thumb|300px|Суффиксное дерево для сжатой строки]] | ||
* Строка <tex>s</tex> разбивается на пары подряд идущих символов: <tex> \langle 12\rangle \langle 11\rangle \langle 12\rangle \langle 21\rangle \langle 22\rangle \langle 21\rangle </tex> | * Строка <tex>s</tex> разбивается на пары подряд идущих символов: <tex> \langle 12\rangle \langle 11\rangle \langle 12\rangle \langle 21\rangle \langle 22\rangle \langle 21\rangle </tex> | ||
| − | *: (если символов | + | *: (если символов нечётное число {{---}} последняя пара дополняется специальным символом <tex>\$</tex>). |
| − | * Пары сортируются устойчивой | + | * Пары сортируются устойчивой сортировкой (удобно сортировать [[Цифровая_сортировка | поразрядной]], так как число разрядов мало, размер алфавита — <tex>O(n)</tex>, то время работы сортировки — линейное): <tex> \langle 11 \rangle \langle 12\rangle \langle 12\rangle \langle 21\rangle \langle 21\rangle \langle22\rangle </tex>. |
* Удаляются копии: <tex> \langle 11\rangle \langle 12\rangle \langle 21\rangle \langle 22\rangle </tex>. | * Удаляются копии: <tex> \langle 11\rangle \langle 12\rangle \langle 21\rangle \langle 22\rangle </tex>. | ||
| − | * Парам даются номера (условно, в массиве они и так есть): <tex>\langle 11 \rangle -(0), \langle 12\rangle -(1), \langle 21\rangle - (2), \langle 22\rangle-(3)</tex> | + | * Парам даются номера (условно, в массиве они и так есть): <tex>\langle 11 \rangle -(0), \langle 12\rangle -(1), \langle 21\rangle - (2), \langle 22\rangle-(3)</tex>. |
| − | * В исходной строке пары заменяются на номера: <tex>1 0 1 2 3 2</tex> | + | * В исходной строке пары заменяются на номера: <tex>1 0 1 2 3 2</tex>. |
| − | * Из полученной строки вдвое меньшего размера рекурсивно создаётся [[Сжатое суффиксное дерево | суффикcное дерево]] тем же алгоритмом | + | * Из полученной строки вдвое меньшего размера рекурсивно создаётся [[Сжатое суффиксное дерево | суффикcное дерево]] тем же алгоритмом. |
| − | + | * Рекурсия не продолжается, если строка имеет длину, равную единице: суффиксное дерево строится тривиально. | |
| − | |||
| − | |||
| − | * | ||
=== Шаг 2: построение чётного дерева === | === Шаг 2: построение чётного дерева === | ||
{{Определение | {{Определение | ||
| − | |definition= | + | |definition= Чётное дерево <tex>T^{even}_s</tex> является деревом суффиксов для строки <tex>s</tex>, узлы-листья |
| − | которого ограничены | + | которого ограничены чётными позициями <tex>0, 2, 4, 6, \dots </tex> строки <tex>s\$</tex>.}} |
| + | |||
| + | [[Файл:Tree101232even-pre.png|thumb|300px|Раскрываем все пары в суффиксы]] | ||
| + | [[Файл:Tree101232even.png|thumb|300px|Корректируем все развилки дерева]] | ||
Из дерева сжатой строки получаем частичное (чётное) дерево исходной строки. Частичное оно потому, что в нём будет только половина суффиксов, то есть те, которые стоят в чётных позициях. | Из дерева сжатой строки получаем частичное (чётное) дерево исходной строки. Частичное оно потому, что в нём будет только половина суффиксов, то есть те, которые стоят в чётных позициях. | ||
| − | Номер каждой пары превращается в номер | + | Номер каждой пары превращается в номер чётного суффикса исходной строки. Раскрываем все пары в суффиксы, из-за чего номера в листьях от этого умножатся на <tex>2</tex> очевидным образом. |
| + | |||
| + | Корректируем все развилки дерева (так как они могут совпадать в первых символах): | ||
| + | для всех внутренних вершин <tex>u</tex>, ребра всех детей которых начинаются с одинаковых символов, мы создадим новую вершину между <tex>u</tex> и ее детьми. Это можно сделать быстро, так как все ребра, исходящие из любой вершины, лексикографически отсортированы по своим первым двум символам (так как мы сортировали номера пар на прошлом шаге). Для каждого ребра нам достаточно проверить, что его первый символ соответствует первому символу соседнего ребра, и, если так, сделать необходимые исправления. Может случиться, что ребра ко всем детям <tex>u</tex> начинаются с одинакового символа, и в этом случае у вершины <tex>u</tex> будет только один ребенок. Тогда удалим <tex>u</tex>. | ||
| + | Эта процедура требует константное время на каждое ребро и константное время на каждую вершину, а значит, на нее требуется линейное время. | ||
| + | |||
| + | Итак, если <tex>T(n)</tex> {{---}} это время, которое потребуется нашему алгоритму, чтобы построить суффиксное дерево для строки <tex>S</tex>, то <tex>T_{even}</tex> может быть построено за время <tex>T(n/2) + O(n)</tex> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === Шаг 3: построение | + | === Шаг 3: построение нечётного по чётному === |
{{Определение | {{Определение | ||
|definition= Нечётное дерево <tex>T^{odd}_s</tex> является деревом суффиксов для строки <tex>s</tex>, узлы-листья | |definition= Нечётное дерево <tex>T^{odd}_s</tex> является деревом суффиксов для строки <tex>s</tex>, узлы-листья | ||
| − | которого ограничены | + | которого ограничены нечётными позициями <tex>1,3,5, \dots </tex> строки <tex>s\$</tex>.}} |
| + | |||
| + | [[Файл:Odd.png|thumb|450px|Нечётное дерево]] | ||
Из чётного дерева нужно получить нечётное дерево (дерево из суффиксов в нечётных позициях). | Из чётного дерева нужно получить нечётное дерево (дерево из суффиксов в нечётных позициях). | ||
| Строка 54: | Строка 63: | ||
* [[Сжатое_суффиксное_дерево#.D0.9F.D0.BE.D1.81.D1.82.D1.80.D0.BE.D0.B5.D0.BD.D0.B8.D0.B5_.D0.B8.D0.B7_.D1.81.D1.83.D1.84.D1.84.D0.B8.D0.BA.D1.81.D0.BD.D0.BE.D0.B3.D0.BE_.D0.BC.D0.B0.D1.81.D1.81.D0.B8.D0.B2.D0.B0 | Строим по чётному дереву суффиксный массив]] — это можно сделать за <tex>О(n)</tex>. | * [[Сжатое_суффиксное_дерево#.D0.9F.D0.BE.D1.81.D1.82.D1.80.D0.BE.D0.B5.D0.BD.D0.B8.D0.B5_.D0.B8.D0.B7_.D1.81.D1.83.D1.84.D1.84.D0.B8.D0.BA.D1.81.D0.BD.D0.BE.D0.B3.D0.BE_.D0.BC.D0.B0.D1.81.D1.81.D0.B8.D0.B2.D0.B0 | Строим по чётному дереву суффиксный массив]] — это можно сделать за <tex>О(n)</tex>. | ||
* Дописываем ко всем суффиксам (кроме того, что на нулевой позиции) символ, предшествующий ему в строке. | * Дописываем ко всем суффиксам (кроме того, что на нулевой позиции) символ, предшествующий ему в строке. | ||
| − | * Заметим, что все | + | * Заметим, что все нечётные суффиксы представляют собой один символ, за которым дальше следует чётный суффикс. А чётные суффиксы у нас уже были отсортированы в суффиксном массиве. Тогда отсортируем их по первому символу за линейное время. |
* [[Сжатое_суффиксное_дерево#.D0.9F.D0.BE.D1.81.D1.82.D1.80.D0.BE.D0.B5.D0.BD.D0.B8.D0.B5_.D0.B8.D0.B7_.D1.81.D1.83.D1.84.D1.84.D0.B8.D0.BA.D1.81.D0.BD.D0.BE.D0.B3.D0.BE_.D0.BC.D0.B0.D1.81.D1.81.D0.B8.D0.B2.D0.B0 | Построим из нового суффиксного массива дерево]], которое будет уже нечётным, что тоже делается за линейное время. | * [[Сжатое_суффиксное_дерево#.D0.9F.D0.BE.D1.81.D1.82.D1.80.D0.BE.D0.B5.D0.BD.D0.B8.D0.B5_.D0.B8.D0.B7_.D1.81.D1.83.D1.84.D1.84.D0.B8.D0.BA.D1.81.D0.BD.D0.BE.D0.B3.D0.BE_.D0.BC.D0.B0.D1.81.D1.81.D0.B8.D0.B2.D0.B0 | Построим из нового суффиксного массива дерево]], которое будет уже нечётным, что тоже делается за линейное время. | ||
| − | + | Таким образом, <tex>T_{odd}</tex> может быть построено за линейное время по <tex>T_{even}</tex>. | |
| − | |||
| − | + | === Шаг 4: слияние чётного и нечётного дерева === | |
| − | + | [[Файл:Tree101232merged-pre.png|thumb|450px|Слитое дерево (условно)]] | |
| + | [[Файл:Tree101232merged-next.png|thumb|450px|Слитое дерево (в упрощённом виде)]] | ||
| − | Далее необходимо найти эффективный способ слияния | + | Далее необходимо найти эффективный способ слияния нечётного и чётного деревьев в одно дерево <tex>T_s</tex>. Слияние будем производить начиная с корней деревьев. |
| − | Предположим, что для каждого узла деревьев <tex>T_s^{odd}</tex> и <tex>T_s^{even}</tex> выходящие из них ребра занесены в специальные списки, где они '''упорядочены''' в возрастающем лексикографическом порядке подстрок, которые представляют эти ребра. Пусть каждое ребро будет дополнительно "помечено" своим первым символом. Возьмем по одному ребру из этих списков с одинаковыми метками (в одном списке не может быть ребер с одинаковыми метками, так как это сжатые суффиксные деревья), обработаем их и рекурсивно спустимся в их поддеревья. Если для ребра из одного списка не оказалось ребра с такой же меткой из другого, то в поддеревья | + | Предположим, что для каждого узла деревьев <tex>T_s^{odd}</tex> и <tex>T_s^{even}</tex> выходящие из них ребра занесены в специальные списки, где они '''упорядочены''' в возрастающем лексикографическом порядке подстрок, которые представляют эти ребра. Пусть каждое ребро будет дополнительно "помечено" своим первым символом. Возьмем по одному ребру из этих списков с одинаковыми метками (в одном списке не может быть ребер с одинаковыми метками, так как это сжатые суффиксные деревья), обработаем их и рекурсивно спустимся в их поддеревья. Если для ребра из одного списка не оказалось ребра с такой же меткой из другого, то в поддеревья не спускаемся, так как там нечего сливать. |
Очевидно, манипуляции со списками работают за линейное время, так как сами списки упорядочены лексикографически. | Очевидно, манипуляции со списками работают за линейное время, так как сами списки упорядочены лексикографически. | ||
Алгоритм просматривает только первые буквы подстрок, представленных ребрами деревьев <tex>T_s^{odd}</tex> и <tex>T_s^{even}</tex>, пусть это будут буквы <tex>\lambda^{odd}</tex> и <tex>\lambda^{even}</tex>. Тогда: | Алгоритм просматривает только первые буквы подстрок, представленных ребрами деревьев <tex>T_s^{odd}</tex> и <tex>T_s^{even}</tex>, пусть это будут буквы <tex>\lambda^{odd}</tex> и <tex>\lambda^{even}</tex>. Тогда: | ||
* если <tex>\lambda^{odd}</tex> <tex>\ne</tex> <tex>\lambda^{even}</tex>, определяется поддерево, соответствующее меньшей из этих букв, и без изменений присоединяется к узлу-родителю; | * если <tex>\lambda^{odd}</tex> <tex>\ne</tex> <tex>\lambda^{even}</tex>, определяется поддерево, соответствующее меньшей из этих букв, и без изменений присоединяется к узлу-родителю; | ||
| − | * если <tex>\lambda^{odd}</tex> <tex>=</tex> <tex>\lambda^{even}</tex> и длины подстрок, представленных соответствующими ребрами, равны, в дерево слияния к текущему узлу добавляются два сына: один {{---}} из | + | * если <tex>\lambda^{odd}</tex> <tex>=</tex> <tex>\lambda^{even}</tex> и длины подстрок, представленных соответствующими ребрами, равны, в дерево слияния к текущему узлу добавляются два сына: один {{---}} из чётного дерева, другой {{---}} из нечётного; |
* если <tex>\lambda^{odd}</tex> <tex>=</tex> <tex>\lambda^{even}</tex> и длины подстрок, представленных соответствующими ребрами, различны, в дерево слияния к текущему узлу добавляются два узла, находящиеся на одном нисходящем пути, при этом ближайший узел будет соответствовать более короткой подстроке. | * если <tex>\lambda^{odd}</tex> <tex>=</tex> <tex>\lambda^{even}</tex> и длины подстрок, представленных соответствующими ребрами, различны, в дерево слияния к текущему узлу добавляются два узла, находящиеся на одном нисходящем пути, при этом ближайший узел будет соответствовать более короткой подстроке. | ||
Поскольку мы рассматриваем только первый символ каждого ребра (то есть делаем вид, что ребра равны, если первые символы у них равны), мы можем иногда слить рёбра, которые не должны были быть слиты. Однако те, которые надо было слить, точно сольем. | Поскольку мы рассматриваем только первый символ каждого ребра (то есть делаем вид, что ребра равны, если первые символы у них равны), мы можем иногда слить рёбра, которые не должны были быть слиты. Однако те, которые надо было слить, точно сольем. | ||
| − | Если начать эту процедуру для корней нечётного и чётного деревьев, она рекурсивно выполнится для корней всех поддеревьев, которые, возможно, уже содержат узлы из | + | Если начать эту процедуру для корней нечётного и чётного деревьев, она рекурсивно выполнится для корней всех поддеревьев, которые, возможно, уже содержат узлы из нечётного и чётного деревьев, поскольку ранее мог быть реализован случай <tex>\lambda^{odd}</tex> <tex>=</tex> <tex>\lambda^{even}</tex>. Так как время манипулирования любым ребром этих деревьев фиксировано, то общее время слияния деревьев составит <tex>O(N)</tex>. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
В результате описанных действий получится дерево <tex>M_x</tex>, в котором будут присутствовать поддеревья, которые прошли процедуру слияния, и которые ее избежали (то есть были перенесены в дерево <tex>M_x</tex> без изменений). | В результате описанных действий получится дерево <tex>M_x</tex>, в котором будут присутствовать поддеревья, которые прошли процедуру слияния, и которые ее избежали (то есть были перенесены в дерево <tex>M_x</tex> без изменений). | ||
| Строка 88: | Строка 90: | ||
=== Шаг 5: удаление двойных дуг === | === Шаг 5: удаление двойных дуг === | ||
| − | + | [[Файл:Tree101232merged.png|thumb|500px|Откорректированное дерево строки <tex>121112212221</tex>]] | |
| − | + | [[Файл:Treestep5_1.jpg|thumb|550px|Пример]] | |
| − | + | Разбираемся с двойными дугами (в примере их три). Для этого мы должны выяснить, сколько начальных символов у них совпадает. Совпадать может любое число символов, даже все. Проверять их все по очереди нельзя, так как это даст квадратичное время. | |
| − | + | Если дуги совпадают полностью, тогда просто удаляем одну из копий. Если начало для двух дуг совпадает только частично, тогда нужно сделать для них общее начало, а ветки, которые на концах, снова развести по разным деревьям (для этого можно во время слияния запомнить их начальный цвет или просто сохранить ссылки на исходные ветки). | |
| + | Рассмотрим то, как это сделать, на примере строки <tex>10010010101000</tex>: | ||
| − | Для | + | Для того чтобы узнать общее начало двойной дуги, нужно взять одну чётную и одну нечётную вершину на дереве, для которых родителем является конец нашей двойной дуги. Например, на рисунке выше двойная дуга <tex>(1)</tex> (конец помечен зелёным) является общим родителем для вершин <tex>3</tex> и <tex>6</tex>. Чтобы узнать, на каком расстоянии будет расслаиваться двойная дуга, надо увеличить номера вершин на единицу и найти их родителя. Он будет находиться на единицу ближе к корню (и путь у вершин будет одинаковой строкой, не считая размера). Родитель вершин <tex>4</tex> и <tex>7</tex> помечен жёлтым, он находится на расстоянии <tex>1</tex> от корня, следовательно, дуга <tex>(1)</tex> должна расслаиваться в двух символах от корня, то есть обе дуги совпадают и их просто надо слить. |
| − | + | Разберём дуги по порядку: | |
| − | |||
| − | + | # Расслоение находится на расстоянии <tex>2</tex> от корня, то есть дуга не расслаивается. | |
| + | # Конец является родителем вершин <tex>2</tex>, <tex>7</tex>. Родитель <tex>3</tex>, <tex>8</tex> после слияния дуги <tex>(1)</tex>, находится на глубине <tex>2</tex> символа. Значит, дуга <tex>(2)</tex> расслаивается на глубине <tex>3</tex> символа, то есть также не расслаивается. Дугу <tex>(2)</tex> нужно вычислять после обработки дуги <tex>(1)</tex>, потому что конец дуги <tex>(1)</tex> после обработки может оказаться на разной высоте, в зависимости от того на каком символе она расслоилась. | ||
| + | # Конец является родителем <tex>2</tex>, <tex>9</tex>. Родитель <tex>3</tex>, <tex>10</tex> находится на расстоянии <tex>3</tex>, а наше расслоение на расстоянии <tex>4</tex>, то есть сливается первый символ двойной дуги. Дугу <tex>(3)</tex> надо вычислять после дуги <tex>(2)</tex>. Потому что если на дуге <tex>(2)</tex> появится разветвление, то компоненты дуги <tex>(3)</tex> придётся растащить по разным веткам дерева и сравнивать их будет не нужно. | ||
| + | # Конец является родителем <tex>1</tex>, <tex>4</tex>. Расслаивается на втором символе. | ||
| + | # Конец является родителем <tex>0</tex>, <tex>3</tex>. Дугу <tex>(5)</tex> можно обрабатывать только после дуги <tex>(4)</tex>, так как от неё будет зависеть глубина расслоения. | ||
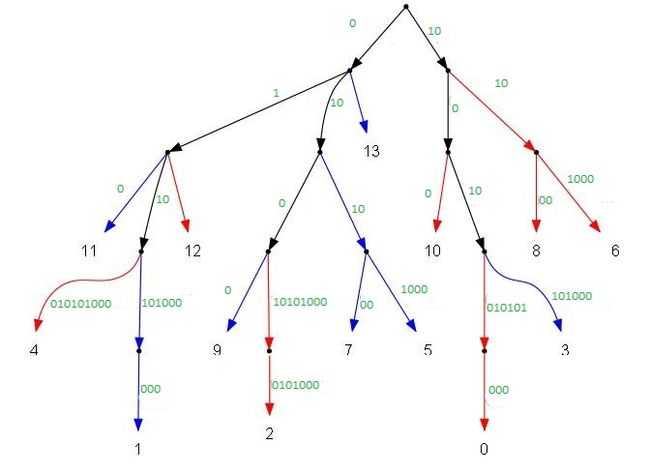
| − | + | [[Файл:Treestep5_2.jpg|thumb|center|650px|Итоговое дерево строки <tex>10010010101000</tex>]] | |
| − | + | Дерево строится рекурсивно, каждый раз длина строки уменьшается вдвое, а все фазы работают линейно. | |
| − | + | В итоге получается <tex> T(n) = T(n / 2) + \Theta (n) = \Theta (n) </tex>. | |
| − | |||
| − | |||
| − | |||
| + | ==Сравнение с другими алгоритмами== | ||
| − | + | ===Достоинства=== | |
| − | + | *Алгоритм Фараха является первым, имеющим асимптотически оптимальное время построения <tex>O(N)</tex> для строк длины <tex>N</tex> над полиномиальным алфавитом, то есть алфавитом мощности порядка <tex>O(N)</tex>. | |
| − | + | ===Недостатки=== | |
| − | |||
| − | + | *Данный алгоритм является больше теоретическим, нежели практическим. Как можно было заметить, основная идея алгоритма довольно проста и понятна. И хоть он и является асимптотически оптимальным, на практике его используют довольно редко. Это связано с тем, что алгоритм весьма сложен для реализации по сравнению с другими алгоритмами построения суффиксных деревьев, а также требует достаточно большой объем памяти. | |
| + | *Является offline-алгоритмом, то есть требует для начала работы всю строку целиком. | ||
==См. также== | ==См. также== | ||
| Строка 126: | Строка 130: | ||
== Источники информации == | == Источники информации == | ||
*[http://www.cs.rutgers.edu/~farach/pubs/Suffix.pdf Optimal suffix tree construction with large alphabets ] | *[http://www.cs.rutgers.edu/~farach/pubs/Suffix.pdf Optimal suffix tree construction with large alphabets ] | ||
| − | *[http://www.proteus2001.narod.ru/gen/txt/11/farach.html Суффиксное дерево {{---}} Алгоритм | + | *[http://www.proteus2001.narod.ru/gen/txt/11/farach.html Суффиксное дерево {{---}} Алгоритм Фараха] |
*[http://books.google.ru/books/about/Computing_Patterns_in_Strings.html?id=iKR0EewiCu4C&redir_esc=y Computing Patterns in Strings] | *[http://books.google.ru/books/about/Computing_Patterns_in_Strings.html?id=iKR0EewiCu4C&redir_esc=y Computing Patterns in Strings] | ||
*[https://github.com/krzysztofp/Text-Algorithms/tree/master/Farach%20suffix%20tree Chris Parjaszewski's implementation] | *[https://github.com/krzysztofp/Text-Algorithms/tree/master/Farach%20suffix%20tree Chris Parjaszewski's implementation] | ||
Текущая версия на 19:21, 4 сентября 2022
Алгоритм Фараха, разработанный в 1997 году американским ученым Мартином Фарах-Колтоном (Martin Farach-Colton) — алгоритм построения суффиксного дерева для заданной строки длины . Сам алгоритм выполняется за время , причём даже не требуется выполнение условия конечности алфавита. Такая эффективность достигается за счёт того, что строковые последовательности определяются на индексированном алфавите или, что эквивалентно, на целочисленном алфавите . При этом накладывается дополнительное условие, что . Такие алфавиты часто встречаются на практике. Важно помнить, что алгоритм скорее теоретический, нежели практический, а основная его ценность заключается в том, что размер алфавита может быть произвольным.
Содержание
Описание алгоритма
Идея алгоритма состоит в том, что мы уменьшаем размер исходной строки, строим суффиксное дерево для неё рекурсивно, а потом получаем из построенного дерево для текущей строки. Для этого мы разбиваем символы исходной строки на пары и нумеруем их, а из полученных номеров составляем новую строку, которая уже в раза короче.
Алгоритм Фараха будет описан в виде пяти выполняемых шагов. Используем в качестве примера строку , определенную на алфавите (в этом примере ).
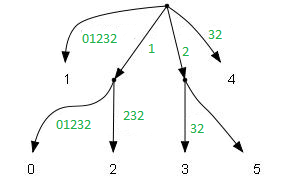
Шаг 1: суффиксное дерево для сжатой строки
- Строка разбивается на пары подряд идущих символов:
- (если символов нечётное число — последняя пара дополняется специальным символом ).
- Пары сортируются устойчивой сортировкой (удобно сортировать поразрядной, так как число разрядов мало, размер алфавита — , то время работы сортировки — линейное): .
- Удаляются копии: .
- Парам даются номера (условно, в массиве они и так есть): .
- В исходной строке пары заменяются на номера: .
- Из полученной строки вдвое меньшего размера рекурсивно создаётся суффикcное дерево тем же алгоритмом.
- Рекурсия не продолжается, если строка имеет длину, равную единице: суффиксное дерево строится тривиально.
Шаг 2: построение чётного дерева
| Определение: |
| Чётное дерево является деревом суффиксов для строки , узлы-листья которого ограничены чётными позициями строки . |
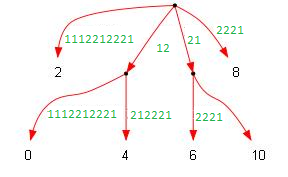
Из дерева сжатой строки получаем частичное (чётное) дерево исходной строки. Частичное оно потому, что в нём будет только половина суффиксов, то есть те, которые стоят в чётных позициях.
Номер каждой пары превращается в номер чётного суффикса исходной строки. Раскрываем все пары в суффиксы, из-за чего номера в листьях от этого умножатся на очевидным образом.
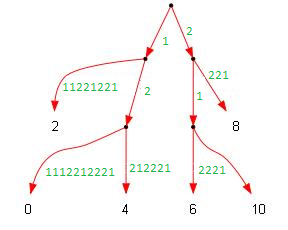
Корректируем все развилки дерева (так как они могут совпадать в первых символах): для всех внутренних вершин , ребра всех детей которых начинаются с одинаковых символов, мы создадим новую вершину между и ее детьми. Это можно сделать быстро, так как все ребра, исходящие из любой вершины, лексикографически отсортированы по своим первым двум символам (так как мы сортировали номера пар на прошлом шаге). Для каждого ребра нам достаточно проверить, что его первый символ соответствует первому символу соседнего ребра, и, если так, сделать необходимые исправления. Может случиться, что ребра ко всем детям начинаются с одинакового символа, и в этом случае у вершины будет только один ребенок. Тогда удалим . Эта процедура требует константное время на каждое ребро и константное время на каждую вершину, а значит, на нее требуется линейное время.
Итак, если — это время, которое потребуется нашему алгоритму, чтобы построить суффиксное дерево для строки , то может быть построено за время
Шаг 3: построение нечётного по чётному
| Определение: |
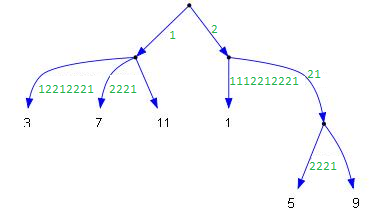
| Нечётное дерево является деревом суффиксов для строки , узлы-листья которого ограничены нечётными позициями строки . |
Из чётного дерева нужно получить нечётное дерево (дерево из суффиксов в нечётных позициях).
- Строим по чётному дереву суффиксный массив — это можно сделать за .
- Дописываем ко всем суффиксам (кроме того, что на нулевой позиции) символ, предшествующий ему в строке.
- Заметим, что все нечётные суффиксы представляют собой один символ, за которым дальше следует чётный суффикс. А чётные суффиксы у нас уже были отсортированы в суффиксном массиве. Тогда отсортируем их по первому символу за линейное время.
- Построим из нового суффиксного массива дерево, которое будет уже нечётным, что тоже делается за линейное время.
Таким образом, может быть построено за линейное время по .
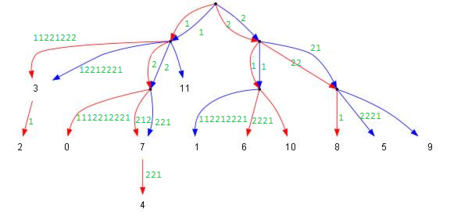
Шаг 4: слияние чётного и нечётного дерева
Далее необходимо найти эффективный способ слияния нечётного и чётного деревьев в одно дерево . Слияние будем производить начиная с корней деревьев. Предположим, что для каждого узла деревьев и выходящие из них ребра занесены в специальные списки, где они упорядочены в возрастающем лексикографическом порядке подстрок, которые представляют эти ребра. Пусть каждое ребро будет дополнительно "помечено" своим первым символом. Возьмем по одному ребру из этих списков с одинаковыми метками (в одном списке не может быть ребер с одинаковыми метками, так как это сжатые суффиксные деревья), обработаем их и рекурсивно спустимся в их поддеревья. Если для ребра из одного списка не оказалось ребра с такой же меткой из другого, то в поддеревья не спускаемся, так как там нечего сливать. Очевидно, манипуляции со списками работают за линейное время, так как сами списки упорядочены лексикографически.
Алгоритм просматривает только первые буквы подстрок, представленных ребрами деревьев и , пусть это будут буквы и . Тогда:
- если , определяется поддерево, соответствующее меньшей из этих букв, и без изменений присоединяется к узлу-родителю;
- если и длины подстрок, представленных соответствующими ребрами, равны, в дерево слияния к текущему узлу добавляются два сына: один — из чётного дерева, другой — из нечётного;
- если и длины подстрок, представленных соответствующими ребрами, различны, в дерево слияния к текущему узлу добавляются два узла, находящиеся на одном нисходящем пути, при этом ближайший узел будет соответствовать более короткой подстроке.
Поскольку мы рассматриваем только первый символ каждого ребра (то есть делаем вид, что ребра равны, если первые символы у них равны), мы можем иногда слить рёбра, которые не должны были быть слиты. Однако те, которые надо было слить, точно сольем.
Если начать эту процедуру для корней нечётного и чётного деревьев, она рекурсивно выполнится для корней всех поддеревьев, которые, возможно, уже содержат узлы из нечётного и чётного деревьев, поскольку ранее мог быть реализован случай . Так как время манипулирования любым ребром этих деревьев фиксировано, то общее время слияния деревьев составит .
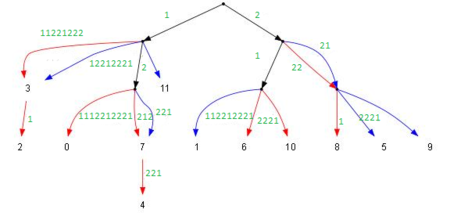
В результате описанных действий получится дерево , в котором будут присутствовать поддеревья, которые прошли процедуру слияния, и которые ее избежали (то есть были перенесены в дерево без изменений).
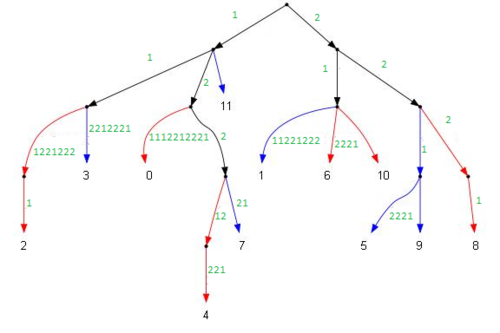
Шаг 5: удаление двойных дуг
Разбираемся с двойными дугами (в примере их три). Для этого мы должны выяснить, сколько начальных символов у них совпадает. Совпадать может любое число символов, даже все. Проверять их все по очереди нельзя, так как это даст квадратичное время. Если дуги совпадают полностью, тогда просто удаляем одну из копий. Если начало для двух дуг совпадает только частично, тогда нужно сделать для них общее начало, а ветки, которые на концах, снова развести по разным деревьям (для этого можно во время слияния запомнить их начальный цвет или просто сохранить ссылки на исходные ветки).
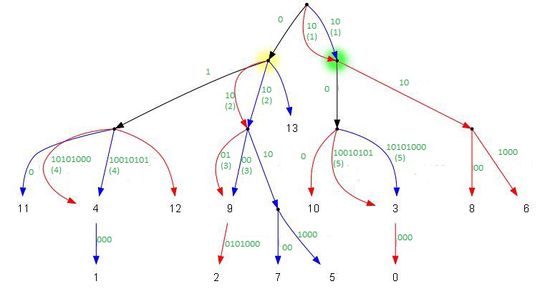
Рассмотрим то, как это сделать, на примере строки :
Для того чтобы узнать общее начало двойной дуги, нужно взять одну чётную и одну нечётную вершину на дереве, для которых родителем является конец нашей двойной дуги. Например, на рисунке выше двойная дуга (конец помечен зелёным) является общим родителем для вершин и . Чтобы узнать, на каком расстоянии будет расслаиваться двойная дуга, надо увеличить номера вершин на единицу и найти их родителя. Он будет находиться на единицу ближе к корню (и путь у вершин будет одинаковой строкой, не считая размера). Родитель вершин и помечен жёлтым, он находится на расстоянии от корня, следовательно, дуга должна расслаиваться в двух символах от корня, то есть обе дуги совпадают и их просто надо слить.
Разберём дуги по порядку:
- Расслоение находится на расстоянии от корня, то есть дуга не расслаивается.
- Конец является родителем вершин , . Родитель , после слияния дуги , находится на глубине символа. Значит, дуга расслаивается на глубине символа, то есть также не расслаивается. Дугу нужно вычислять после обработки дуги , потому что конец дуги после обработки может оказаться на разной высоте, в зависимости от того на каком символе она расслоилась.
- Конец является родителем , . Родитель , находится на расстоянии , а наше расслоение на расстоянии , то есть сливается первый символ двойной дуги. Дугу надо вычислять после дуги . Потому что если на дуге появится разветвление, то компоненты дуги придётся растащить по разным веткам дерева и сравнивать их будет не нужно.
- Конец является родителем , . Расслаивается на втором символе.
- Конец является родителем , . Дугу можно обрабатывать только после дуги , так как от неё будет зависеть глубина расслоения.
Дерево строится рекурсивно, каждый раз длина строки уменьшается вдвое, а все фазы работают линейно. В итоге получается .
Сравнение с другими алгоритмами
Достоинства
- Алгоритм Фараха является первым, имеющим асимптотически оптимальное время построения для строк длины над полиномиальным алфавитом, то есть алфавитом мощности порядка .
Недостатки
- Данный алгоритм является больше теоретическим, нежели практическим. Как можно было заметить, основная идея алгоритма довольно проста и понятна. И хоть он и является асимптотически оптимальным, на практике его используют довольно редко. Это связано с тем, что алгоритм весьма сложен для реализации по сравнению с другими алгоритмами построения суффиксных деревьев, а также требует достаточно большой объем памяти.
- Является offline-алгоритмом, то есть требует для начала работы всю строку целиком.