Биномиальная куча — различия между версиями
Zemskovk (обсуждение | вклад) (→Персистентность) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 10 промежуточных версий 6 участников) | |||
| Строка 5: | Строка 5: | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | '''Биномиальное дерево <tex>B_k</tex>''' (англ. ''binomial tree'') {{---}} [[Дерево, эквивалентные определения|дерево]], определяемое для каждого <tex>k = 0, 1, 2, \dots </tex> следующим образом: <tex>B_0</tex> {{---}} дерево, состоящее из одного узла; <tex>B_k</tex> состоит из двух биномиальных деревьев <tex>B_{k-1}</tex>, | + | '''Биномиальное дерево <tex>B_k</tex>''' (англ. ''binomial tree'') {{---}} [[Дерево, эквивалентные определения|дерево]], определяемое для каждого <tex>k = 0, 1, 2, \dots </tex> следующим образом: <tex>B_0</tex> {{---}} дерево, состоящее из одного узла; <tex>B_k</tex> состоит из двух биномиальных деревьев <tex>B_{k-1}</tex>, связанных вместе таким образом, что корень одного из них является дочерним узлом корня второго дерева. |
}} | }} | ||
| Строка 166: | Строка 166: | ||
Рассмотрим пошагово алгоритм: | Рассмотрим пошагово алгоритм: | ||
* Найдем биномиальное дерево с минимальным корневым значением. Предположим, что это дерево <tex>B_k</tex>. Время работы этого шага алгоритма <tex>\Theta(\log n)</tex>. | * Найдем биномиальное дерево с минимальным корневым значением. Предположим, что это дерево <tex>B_k</tex>. Время работы этого шага алгоритма <tex>\Theta(\log n)</tex>. | ||
| − | * Удаляем дерево <tex>B_k</tex> из кучи <tex>H</tex>. Иными словами удаляем его корень из списка корней кучи. Это можно сделать за время <tex>O(1)</tex>. | + | * Удаляем дерево <tex>B_k</tex> из кучи <tex>H</tex>. Иными словами, удаляем его корень из списка корней кучи. Это можно сделать за время <tex>O(1)</tex>. |
* Пусть <tex>H'</tex> {{---}} куча детей найденного корня. При этом мы для каждого из ребенка устанавливаем указатель на предка равным <tex>null</tex>. После этого сливаем кучу <tex>H'</tex> c <tex>H</tex> за <tex>\Omega(\log n)</tex>. | * Пусть <tex>H'</tex> {{---}} куча детей найденного корня. При этом мы для каждого из ребенка устанавливаем указатель на предка равным <tex>null</tex>. После этого сливаем кучу <tex>H'</tex> c <tex>H</tex> за <tex>\Omega(\log n)</tex>. | ||
| − | Процедура выполняется за время <tex>\Theta(\log n)</tex>, поскольку всего в списке <tex>\Theta(\log n)</tex> корней биномиальных деревьев. И всего у найденного дерева <tex> k </tex> порядка (с минимальным значением ключа) ровно <tex> k </tex> детей, то сложность перебора этих детей будет тоже <tex>\Theta(\log n)</tex>. А процесс слияния выполняется за <tex>\Omega(\log n)</tex>. Таким образом операция выполняется <tex>\Theta(\log n)</tex>. | + | Процедура выполняется за время <tex>\Theta(\log n)</tex>, поскольку всего в списке <tex>\Theta(\log n)</tex> корней биномиальных деревьев. И всего у найденного дерева <tex> k </tex> порядка (с минимальным значением ключа) ровно <tex> k </tex> детей, то сложность перебора этих детей будет тоже <tex>\Theta(\log n)</tex>. А процесс слияния выполняется за <tex>\Omega(\log n)</tex>. Таким образом, операция выполняется <tex>\Theta(\log n)</tex>. |
[[Файл:BinHeapExampleNew31.png|700px|Примеp извлечения минимума]] | [[Файл:BinHeapExampleNew31.png|700px|Примеp извлечения минимума]] | ||
| Строка 231: | Строка 231: | ||
=== Персистентность === | === Персистентность === | ||
| − | Биноминальную кучу можно сделать [[Персистентные структуры данных|персистентной]] при реализации на односвязных списках. Для этого будем хранить список корней в порядке возрастания ранга, а детей будем хранить по убыванию ранга. Каждый родитель будет знать ребенка с большим рангом, который является головой списка детей, но ребенок не будет знать родителя. Односвязанные списки хороши с точки зрения функционального программирования, так как голова списка не будет достижима из потомков. Тогда при добавлениии новой версии в голову или удалении объявляя другую вершину новой головой мы не будем терять старые версии, которые останутся на месте, так как фактически односвязный список с операциями на голове это [[Персистентный стек|персистентный стек]], который является полностью персистентной функциональной структурой. При этом каждая версия будет поддерживать возможность изменения, что является полным уровнем персистентности | + | Биноминальную кучу можно сделать [[Персистентные структуры данных|персистентной]] при реализации на односвязных списках<ref>[https://github.com/kgeorgiy/okasaki/tree/master/Okasaki/Chapter3 Github {{---}} реализация на Haskell]</ref>. Для этого будем хранить список корней в порядке возрастания ранга, а детей будем хранить по убыванию ранга. Каждый родитель будет знать ребенка с большим рангом, который является головой списка детей, но ребенок не будет знать родителя. Односвязанные списки хороши с точки зрения функционального программирования, так как голова списка не будет достижима из потомков. Тогда при добавлениии новой версии в голову или удалении объявляя другую вершину новой головой мы не будем терять старые версии, которые останутся на месте, так как фактически односвязный список с операциями на голове это [[Персистентный стек|персистентный стек]], который является полностью персистентной функциональной структурой. При этом каждая версия будет поддерживать возможность изменения, что является полным уровнем персистентности. Также поддерживается операция <tex>\mathrm {merge}</tex> для всех версий биномиальных куч, что позволяет получать новую версию путём сливания старых. Это добавляет конфлюэнтный уровень персистентности. |
== См. также == | == См. также == | ||
| Строка 239: | Строка 239: | ||
* [[Куча Бродала-Окасаки]] | * [[Куча Бродала-Окасаки]] | ||
| + | ==Примечания== | ||
| + | |||
| + | <references /> | ||
== Источники информации == | == Источники информации == | ||
* [http://ru.wikipedia.org/wiki/Биномиальная_куча Википедия {{---}} Биномиальная куча] | * [http://ru.wikipedia.org/wiki/Биномиальная_куча Википедия {{---}} Биномиальная куча] | ||
* [http://en.wikipedia.org/wiki/Binomial_heap Wikipedia {{---}} Binomial heap] | * [http://en.wikipedia.org/wiki/Binomial_heap Wikipedia {{---}} Binomial heap] | ||
* [http://www.intuit.ru/department/algorithms/dscm/7/ INTUIT.ru {{---}} Биномиальные кучи] | * [http://www.intuit.ru/department/algorithms/dscm/7/ INTUIT.ru {{---}} Биномиальные кучи] | ||
| + | * [http://www.lektorium.tv/lecture/?id=14234 Лекция А.С. Станкевича по приоритетным очередям] | ||
* Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 538—558. — ISBN 5-8489-0857-4 | * Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 538—558. — ISBN 5-8489-0857-4 | ||
Текущая версия на 19:22, 4 сентября 2022
Содержание
Биномиальное дерево
| Определение: |
| Биномиальное дерево (англ. binomial tree) — дерево, определяемое для каждого следующим образом: — дерево, состоящее из одного узла; состоит из двух биномиальных деревьев , связанных вместе таким образом, что корень одного из них является дочерним узлом корня второго дерева. |
Свойства биномиальных деревьев
| Утверждение: |
Биномиальное дерево с вершинами имеет узлов. |
|
Докажем по индукции: База — верно. Пусть для некоторого условие верно, то докажем, что для это также верно: Так как в дереве порядка вдвое больше узлов, чем в дереве порядка , то дерево порядка имеет узлов. Переход доказан, то биномиальное дерево с вершинами имеет узлов. |
| Утверждение: |
Биномиальное дерево с вершинами имеет высоту . |
|
Докажем по индукции: База — верно. Пусть для некоторого условие верно, то докажем, что для это также верно: Так как в дереве порядка высота больше на (так как мы подвешиваем к текущему дереву дерево того же порядка), чем в дереве порядка , то дерево порядка имеет высоту . Переход доказан, то биномиальное дерево с вершинами имеет высоту . |
| Утверждение: |
Биномиальное дерево с вершинами имеет ровно узлов на высоте . |
|
Докажем по индукции: База — верно. Пусть для некоторого условие верно, то докажем, что для это также верно: Рассмотрим уровень дерева . Дерево было получено подвешиванием одного дерева порядка к другому. Тогда на уровне дерева всего узлов , так как от подвешенного дерева в дерево порядка нам пришли узлы глубины . То для -го уровня дерева количество узлов . Переход доказан, то биномиальное дерево с вершинами имеет ровно узлов на высоте . |
| Утверждение: |
Биномиальное дерево с вершинами имеет корень степени ; степень всех остальных вершин меньше степени корня биномиального дерева; |
| Так как в дереве порядка степень корня больше на , чем в дереве порядка , а в дереве нулевого порядка степень корня , то дерево порядка имеет корень степени . И так как при таком увеличении порядка (при переходе от дерева порядка к ) в полученном дереве лишь степень корня возрастает, то доказываемый инвариант, то есть степень корня больше степени остальных вершин, не будет нарушаться. |
| Утверждение: |
В биномиальном дереве с вершинами максимальная степень произвольного узла равна . |
| Докажем это утверждение для корня. Степень остальных вершин меньше по предыдущему свойству. Так как степень корня дерева порядка равна , а узлов в этом дереве , то прологарифмировав обе части получаем, что , то степень произвольного узла не более . |
Биномиальная куча
| Определение: |
Биномиальная куча (англ. binomial heap) представляет собой множество биномиальных деревьев, которые удовлетворяют следующим свойствам:
|
Представление биномиальных куч
Поскольку количество детей у узлов варьируется в широких пределах, ссылка на детей осуществляется через левого ребенка, а остальные дети образуют односвязный список. Каждый узел в биномиальной куче представляется набором полей:
- — ключ (вес) элемента,
- — указатель на родителя узла,
- — указатель на левого ребенка узла,
- — указатель на правого брата узла,
- — степень узла (количество дочерних узлов данного узла).
Корни деревьев, из которых состоит куча, содержатся в так называемом списке корней, при проходе по которому степени соответствующих корней находятся в возрастающем порядке. Доступ к куче осуществляется ссылкой на первый корень в списке корней.
Операции над биномиальными кучами
Рассмотрим операции, которые можно производить с биномиальной кучей. Время работы указано в таблице:
| Операция | Время работы |
|---|---|
Обозначим нашу кучу за . То пусть — указатель на корень биномиального дерева минимального порядка этой кучи. Изначально , то есть куча не содержит элементов.
getMinimum
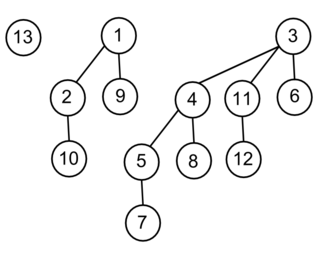
Для нахождения минимального элемента надо найти элемент в списке корней с минимальным значением (предполагается, что ключей, равных , нет).
Так как корней в этом списке не более , то операция выполняется за .
При вызове этой процедуры для кучи, изображенной на картинке ниже, будет возвращен указатель на вершину с ключом .
При использовании указателя на биномиальное дерево, которое содержит минимальный элемент, время для этой операции может быть сведено к . Указатель должен обновляться при выполнении любой операции, кроме . Это может быть сделано за , не ухудшая время работы других операций.
merge
Эта операция, соединяющая две биномиальные кучи в одну, используется в качестве подпрограммы большинством остальных операций.
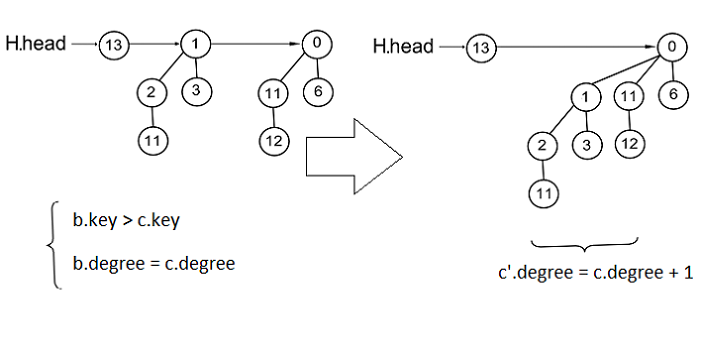
Вот в чем состоит ее суть: пусть есть две биномиальные кучи с и . Размеры деревьев в кучах соответствуют двоичным числам и , то есть при наличии дерева соответствующего порядка в этом разряде числа стоит единица, иначе ноль. При сложении столбиком в двоичной системе происходят переносы, которые соответствуют слияниям двух биномиальных деревьев в дерево . Надо только посмотреть, в каком из сливаемых деревьев корень меньше, и считать его верхним (пример работы для одного случая приведен на рисунке справа; в другом случае подвешиваем наоборот).
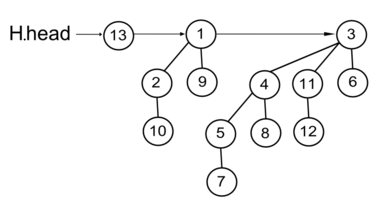
Работа этой процедуры начинается с соединения корневых списков куч в единый список, в котором корневые вершины идут в порядке неубывания их степеней.
В получившемся списке могут встречаться пары соседних вершин одинаковой степени. Поэтому мы начинаем соединять деревья равной степени и делаем это до тех пор, пока деревьев одинаковой степени не останется. Этот процесс соответствует сложению двоичных чисел столбиком, и время его работы пропорционально числу корневых вершин, то есть операция выполняется за .
BinomialHeap merge(H1 : BinomialHeap, H2 : BinomialHeap):
if H1 == null
return H2
if H2 == null
return H1
H.head = null // H — результат слияния
curH = H.head // слияние корневых списков
curH1 = H1.head
curH2 = H2.head
while curH1 != null and curH2 != null
if curH1.degree < curH2.degree
curH.sibling = curH1
curH = curH1
curH1 = curH1.sibling
else
curH.sibling = curH2
curH = curH2
curH2 = curH2.sibling
if curH1 == null
while curH2 != null
curH.sibling = curH2
curH2 = curH2.sibling
else
while curH1 != null
curH.sibling = curH1
curH1 = curH1.sibling
curH = H.head // объединение деревьев одной степени
while curH.sibling != null
if curH.degree == curH.sibling.degree
p[curH] = curH.sibling
tmp = curH.sibling
curH.sibling = curH.sibling.child
curH = tmp
continue
curH = curH.sibling
return H
insert
Чтобы добавить новый элемент в биномиальную кучу нужно создать биномиальную кучу с единственным узлом, содержащим этот элемент, за время и объединить ее с биномиальной кучей за , так как в данном случае куча содержит лишь одно дерево.
extractMin
Приведенная ниже процедура извлекает узел с минимальным ключом из биномиальной кучи и возвращает указатель на извлеченный узел.
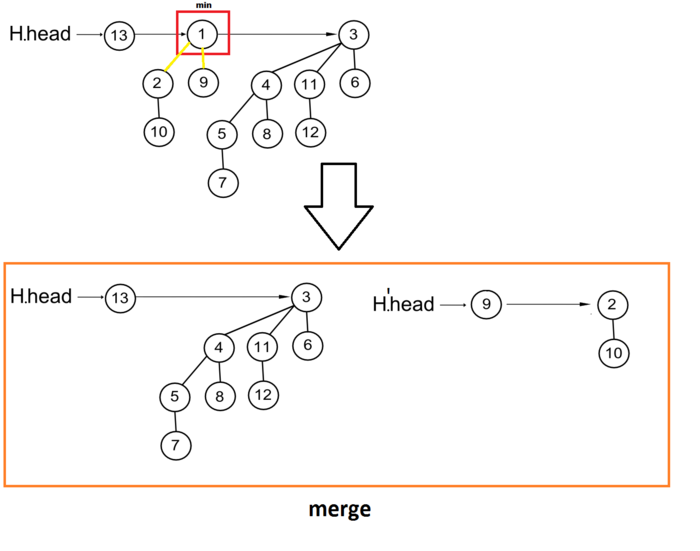
Рассмотрим пошагово алгоритм:
- Найдем биномиальное дерево с минимальным корневым значением. Предположим, что это дерево . Время работы этого шага алгоритма .
- Удаляем дерево из кучи . Иными словами, удаляем его корень из списка корней кучи. Это можно сделать за время .
- Пусть — куча детей найденного корня. При этом мы для каждого из ребенка устанавливаем указатель на предка равным . После этого сливаем кучу c за .
Процедура выполняется за время , поскольку всего в списке корней биномиальных деревьев. И всего у найденного дерева порядка (с минимальным значением ключа) ровно детей, то сложность перебора этих детей будет тоже . А процесс слияния выполняется за . Таким образом, операция выполняется .
Node extractMin(H : BinomialHeap): //поиск корня х с минимальным значением ключа в списке корней Н:
min =
x = null
xBefore = null
curx = H.head
curxBefore = null
while curx != null
if curx.key < min // релаксируем текущий минимум
min = curx.key
x = curx
xBefore = curxBefore
curxBefore = curx
curx = curx.sibling
if xBefore == null //удаление найденного корня x из списка корней деревьев кучи
H.head = x.sibling
else
xBefore.sibling = x.sibling
H' = null //построение кучи детей вершины x, при этом изменяем предка соответствующего ребенка на null:
curx = x.child
H'.head = x.child
while curx != null
p[curx] = null // меняем указатель на родителя узла curx
curx = curx.sibling // переход к следующему ребенку
H = merge(H, H') // слияние нашего дерева с деревом H'
return x
decreaseKey
Следующая процедура уменьшает ключ элемента биномиальной кучи, присваивая ему новое значение. Вершина, ключ которой был уменьшен, «всплывает» как в обычной куче. Процедура выполняется за время , поскольку глубина вершины в худшем случае есть (свойства биномиального дерева), а при выполнении каждого шага алгоритма мы поднимаемся вверх.
function decreaseKey(H : BinomialHeap, x : Node, k : int):
if k > key[x] // проверка на то, что текущий ключ x не меньше передаваемого ключа k
return
key[x] = k
y = x
z = p[y]
while z != null and key[y] < key[z] // поднимаем x с новым ключом k, пока это значение меньше значения в родительской вершине
swap(key[y], key[z])
y = z
z = p[y]
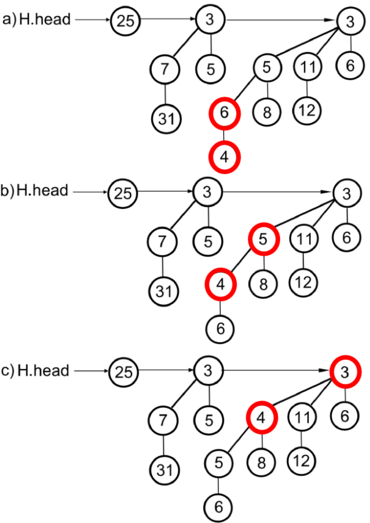
Пример работы процедуры проиллюстрирован на рисунке ( — уменьшаемый элемент, — его предок).
delete
Удаление ключа сводится к операциям и : сначала нужно уменьшить ключ до минимально возможного значения, а затем извлечь вершину с минимальным ключом. В процессе выполнения процедуры этот узел всплывает вверх, откуда и удаляется. Процедура выполняется за время , поскольку каждая из операций, которые используется в реализации, работают за .
function delete(H : BinomialHeap, x : Node):
decreaseKey(H, x, ) // уменьшение ключа до минимально возможного значения
extractMin(H) // удаление "всплывшего" элемента
Персистентность
Биноминальную кучу можно сделать персистентной при реализации на односвязных списках[1]. Для этого будем хранить список корней в порядке возрастания ранга, а детей будем хранить по убыванию ранга. Каждый родитель будет знать ребенка с большим рангом, который является головой списка детей, но ребенок не будет знать родителя. Односвязанные списки хороши с точки зрения функционального программирования, так как голова списка не будет достижима из потомков. Тогда при добавлениии новой версии в голову или удалении объявляя другую вершину новой головой мы не будем терять старые версии, которые останутся на месте, так как фактически односвязный список с операциями на голове это персистентный стек, который является полностью персистентной функциональной структурой. При этом каждая версия будет поддерживать возможность изменения, что является полным уровнем персистентности. Также поддерживается операция для всех версий биномиальных куч, что позволяет получать новую версию путём сливания старых. Это добавляет конфлюэнтный уровень персистентности.
См. также
Примечания
Источники информации
- Википедия — Биномиальная куча
- Wikipedia — Binomial heap
- INTUIT.ru — Биномиальные кучи
- Лекция А.С. Станкевича по приоритетным очередям
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 538—558. — ISBN 5-8489-0857-4