Вещественный двоичный поиск — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 70 промежуточных версий 10 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Вещественный двоичный поиск''' - алгоритм поиска аргумента для заданного значения монотонной вещественной функции. | + | '''Вещественный двоичный поиск''' (англ. ''Bisection method''){{---}} алгоритм поиска аргумента для заданного значения монотонной вещественной функции. |
== Формулировка задачи == | == Формулировка задачи == | ||
| − | Пусть нам задана монотонная функция. Необходимо найти значение аргумента <tex>x</tex> этой функции, | + | Пусть нам задана монотонная функция <tex> f </tex> и какое-то значение <tex> C </tex> этой функции. Необходимо найти значение аргумента <tex> x </tex> этой функции, такое, что <tex> f(x) = C </tex>. |
[[Файл:Function.png]] | [[Файл:Function.png]] | ||
== Решение задачи == | == Решение задачи == | ||
| − | Применим идею двоичного поиска. Выберем такие границы, где значение функции точно больше и точно меньше заданного значения. Выберем значение в середине этого отрезка. Если оно меньше, чем заданное, то сместим левую границу в середину отрезка. В противном случае сместим правую границу. Далее повторим процесс сужения границ. Встает вопрос, когда остановиться. Есть несколько способов сделать это. | + | Применим идею [[целочисленный двоичный поиск | двоичного поиска]]. Выберем такие границы, где значение функции точно больше и точно меньше заданного значения. Выберем значение в середине этого отрезка. Если оно меньше, чем заданное, то сместим левую границу в середину отрезка. В противном случае сместим правую границу. Далее повторим процесс сужения границ. Встает вопрос, когда остановиться. Есть несколько способов сделать это. |
| − | == Способы закончить поиск == | + | === Способы закончить поиск === |
| − | + | {| class="wikitable" | |
| − | + | ! Способы || Плюсы || Минусы || Оценка на число итераций | |
| + | |- | ||
| + | | Окончание, когда рассматриваемый отрезок станет меньше заданной погрешности <tex> \varepsilon </tex>. || Заданная точность найденного значения. || Алгоритм может зациклиться. В компьютере мы работаем с конечным числом вещественных чисел, у которых есть точность. При больших значениях функции длина отрезка может никогда не уменьшиться до заданного значения. || В данном случае нам нужно рассмотреть <tex dpi=130> \genfrac{}{}{}{}{R - L}{\varepsilon} </tex> чисел <tex> \Rightarrow </tex> примерное число итераций <tex dpi=130> \log(\genfrac{}{}{}{}{R - L}{\varepsilon}) </tex>. | ||
| + | |- | ||
| + | | Окончание, когда значение функции на концах отрезках различается менее, чем на заданную погрешность <tex> \varepsilon </tex>. || Значение функции от найденного значения имеет заданную точность. || а) Возможна большая погрешность, если функция будет очень медленно возрастать. <br> б) Может зациклиться по той же причине, что и в первом способе. || Аналогичная с первым случаем логика, примерное число итераций <tex dpi=130> \log(\genfrac{}{}{}{}{f(R) - f(L)}{\varepsilon}) </tex>. | ||
| + | |- | ||
| + | | «Абсолютно точный поиск» <br> Окончание, когда границы отрезка — два соседних по представлению значения в типе данных. Утверждается, что два числа — соседние, если середина их отрезка совпадает или с левой, или с правой границей. || Максимально возможная точность найденного значения. || Возможно плохое поведение, если искомый аргумент равен нулю. || При работе с числами с плавающей точкой количество итераций зависит от плотности чисел на данном отрезке. При работе с числами фиксированной точности <tex>\varepsilon</tex> количество итераций аналогично первому и второму случаю равно <tex dpi=130> \log(\genfrac{}{}{}{}{R - L}{\varepsilon}) </tex>. | ||
| + | |- | ||
| + | | «Итеративный способ» <br> Выполнение конечного числа итераций. || У способа фиксированная погрешность. || Довольно плохая точность, если границы отрезка находятся на большом расстоянии. || Выполняется заданное количество итераций. | ||
| + | |} | ||
| − | + | === Выбор границы отрезка для поиска === | |
| − | + | Для начала найдем левую границу, выберем произвольную отрицательную точку (например <tex>-1</tex>). Будем удваивать ее до тех пор, пока значение в ней будет больше заданного значения. Для того, чтобы найти правую границу, выберем произвольную положительную точку (например <tex>1</tex>). Будем удваивать ее до тех пор, пока значение функции в этой точке меньше заданного. | |
| − | |||
| − | : '''-''' | + | == Псевдокод == |
| − | * | + | '''double''' findLeftBoard(C : '''double'''): |
| − | : ''' | + | x = -1 |
| − | : ''' | + | '''while''' f(x) > C |
| − | + | x = x * 2 | |
| − | : ''' | + | '''return''' x |
| − | + | ||
| − | == | + | . |
| − | + | ||
| + | '''double''' findRightBoard(C : '''double'''): | ||
| + | x = 1 | ||
| + | '''while''' f(x) < C | ||
| + | x = x * 2 | ||
| + | '''return''' x | ||
| + | . | ||
| + | |||
| + | '''double''' binSearch(C : '''double'''): | ||
| + | left = findLeftBoard(C) | ||
| + | right = findRightBoard(C) | ||
| + | '''while''' right - left < eps <font color=green> // Здесь можно использовать другое условие выхода </font> | ||
| + | mid = (left + right) / 2 | ||
| + | '''if''' f(mid) < C | ||
| + | left = mid | ||
| + | '''else''' | ||
| + | right = mid | ||
| + | '''return''' (left + right) / 2 | ||
| + | |||
| + | . | ||
| + | |||
| + | == Метод секущих == | ||
| + | [[Файл:Secant method.png|thumb|350px|right|Метод секущих при <tex> C = 0 </tex>]] | ||
| + | |||
| + | Итерационный численный метод приближённого нахождения корня уравнения. | ||
| + | |||
| + | === Алгоритм === | ||
| + | Пусть нам задана монотонная <tex> f </tex> и значение <tex> C </tex>. Выберем две начальные точки, причем <tex> f(x_{1}) < C </tex>, а <tex> f(x_{2}) > C </tex>. Проведем через них прямую, которая пересечет прямую <tex> y = C </tex> в точке <tex> (x_{3}, C) </tex>. Теперь вместо точек <tex> x_{1} </tex> и <tex> x_{2} </tex> возьмем точки <tex> x_{3} </tex> и <tex> x_{2} </tex>, и проделаем ту же операцию и так далее, получая точки <tex> x_{n+1} </tex> и <tex> x_{n} </tex>, пока <tex> |x_{n-1} - x_{n}| > \varepsilon </tex>. | ||
| + | Вычисляем каждое последующее значение <tex> x_{n+1} </tex> с помощью формулы: | ||
| + | |||
| + | <tex dpi=130> x_{n+1} = x_{n-1} + \dfrac{(C - f(x_{n}))\cdot(x_{n} - x_{n-1})}{f(x_{n}) - f(x_{n-1})} </tex> | ||
| + | |||
| + | Нахождение нулей функции <tex>(C = 0)</tex>: | ||
| + | |||
| + | <tex dpi=130> x_{n+1} = x_{n-1} - \dfrac{f(x_{n})\cdot(x_{n} - x_{n-1})}{f(x_{n}) - f(x_{n-1})} </tex> | ||
| + | |||
| + | === Псевдокод === | ||
| + | <code> | ||
| + | '''double''' search (a : '''double''', b : '''double''', eps : '''double'''): <font color=green> // Где a {{---}} левая граница, а b {{---}} правая </font> | ||
| + | '''while''' |a - b| > eps | ||
| + | a = b - (b - a) * f(b) / (f(b) - f(a)) | ||
| + | b = a - (a - b) * f(a) / (f(a) - f(b)) | ||
| + | '''return''' b | ||
| + | </code> | ||
| + | |||
| + | == Метод Ньютона == | ||
| + | [[Файл:Newton method.png|thumb|300px|right|Метод Ньютона]] | ||
| + | |||
| + | Итерационный численный метод нахождения нуля заданной функции. | ||
| + | |||
| + | === Алгоритм === | ||
| + | Задана монотонная, дифференцируемая функция и начальное значение <tex> x_{0} </tex>. Построим касательную к нашей функции в заданной точке и найдем новую точку <tex> x_{1} </tex>, как пересечения касательной и оси абсцисс. Пока не выполнено заданное условие, например <tex> f(x_{n}) < \varepsilon </tex>, вычисляем новое значение <tex> x_{n+1} </tex> по формуле: | ||
| + | |||
| + | <tex dpi=130> x_{n+1} = x_{n} - \dfrac{f(x_{n})}{f'(x_{n})} </tex> | ||
| + | |||
| + | === Псевдокод === | ||
| + | <code> | ||
| + | '''double''' search (x : '''double''', eps : '''double'''): | ||
| + | '''while''' f(x) > eps | ||
| + | x = x - f(x) / f'(x) | ||
| + | '''return''' x | ||
| + | </code> | ||
| + | |||
| + | === Пример === | ||
| + | Пусть даны числа <tex> C </tex> и <tex> n </tex> {{---}} число и корень какой степень нам нужно посчитать соответственно. Пусть <tex> x = \sqrt[n]{C}</tex>. Возведем все выражение в <tex>n</tex>-ую степень и перенесем всё в левую часть, тогда <tex> x^n - C = 0 </tex>. То есть нужно найти нуль этого выражения, решим это с помощью метода Ньютона. | ||
| + | |||
| + | <code> | ||
| + | '''double''' nthRoot (C : '''double''', n : '''double''', eps : '''double''') | ||
| + | '''while''' pow(x, n) - C > eps | ||
| + | x = x - (pow(x, n) - C) / (n * pow(x, n - 1)) | ||
| + | '''return''' x | ||
| + | </code> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Замечания == | == Замечания == | ||
| − | Необходимо отметить, то функция должна быть строго монотонна, | + | * Необходимо отметить, то функция должна быть строго монотонна, если мы ищем конкретный корень и он единственный. Нестрого монотонна, если нам необходимо найти самый левый (правый) аргумент. Если же функция не монотонна, то данный алгоритм не найдет искомый аргумент, либо найдет аргумент, но он не будет единственным. |
| − | == Источники == | + | * Классической задачей на вещественный двоичный поиск является задача поиска корня <tex>n</tex>-ой степени из числа <tex>x</tex>: <tex>\sqrt[n]{x}</tex>. При <tex>x \geqslant 1</tex> нижней границей для поиска будет <tex>1</tex>, а верхней {{---}} <tex>x</tex>. |
| − | * [http:// | + | |
| + | == См. также == | ||
| + | * [[Целочисленный двоичный поиск]] | ||
| + | |||
| + | == Источники информации == | ||
| + | * [http://en.wikipedia.org/wiki/Bisection_method Bisection method {{---}} Wikipedia] | ||
| + | * [http://en.wikipedia.org/wiki/Newton%27s_method Newton's method {{---}} Wikipedia] | ||
| + | * [http://www.youtube.com/watch?v=qkLLcdgJj_o Видеолекция "сортировка и поиск"] | ||
| + | * [http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=binarySearch Binary search {{---}} Topcoder] | ||
| + | |||
| + | [[Категория: Дискретная математика и алгоритмы]] | ||
| + | [[Категория: Алгоритмы поиска]] | ||
Текущая версия на 19:22, 4 сентября 2022
Вещественный двоичный поиск (англ. Bisection method)— алгоритм поиска аргумента для заданного значения монотонной вещественной функции.
Содержание
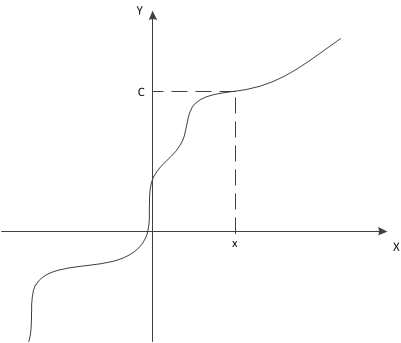
Формулировка задачи
Пусть нам задана монотонная функция и какое-то значение этой функции. Необходимо найти значение аргумента этой функции, такое, что .
Решение задачи
Применим идею двоичного поиска. Выберем такие границы, где значение функции точно больше и точно меньше заданного значения. Выберем значение в середине этого отрезка. Если оно меньше, чем заданное, то сместим левую границу в середину отрезка. В противном случае сместим правую границу. Далее повторим процесс сужения границ. Встает вопрос, когда остановиться. Есть несколько способов сделать это.
Способы закончить поиск
| Способы | Плюсы | Минусы | Оценка на число итераций |
|---|---|---|---|
| Окончание, когда рассматриваемый отрезок станет меньше заданной погрешности . | Заданная точность найденного значения. | Алгоритм может зациклиться. В компьютере мы работаем с конечным числом вещественных чисел, у которых есть точность. При больших значениях функции длина отрезка может никогда не уменьшиться до заданного значения. | В данном случае нам нужно рассмотреть чисел примерное число итераций . |
| Окончание, когда значение функции на концах отрезках различается менее, чем на заданную погрешность . | Значение функции от найденного значения имеет заданную точность. | а) Возможна большая погрешность, если функция будет очень медленно возрастать. б) Может зациклиться по той же причине, что и в первом способе. |
Аналогичная с первым случаем логика, примерное число итераций . |
| «Абсолютно точный поиск» Окончание, когда границы отрезка — два соседних по представлению значения в типе данных. Утверждается, что два числа — соседние, если середина их отрезка совпадает или с левой, или с правой границей. |
Максимально возможная точность найденного значения. | Возможно плохое поведение, если искомый аргумент равен нулю. | При работе с числами с плавающей точкой количество итераций зависит от плотности чисел на данном отрезке. При работе с числами фиксированной точности количество итераций аналогично первому и второму случаю равно . |
| «Итеративный способ» Выполнение конечного числа итераций. |
У способа фиксированная погрешность. | Довольно плохая точность, если границы отрезка находятся на большом расстоянии. | Выполняется заданное количество итераций. |
Выбор границы отрезка для поиска
Для начала найдем левую границу, выберем произвольную отрицательную точку (например ). Будем удваивать ее до тех пор, пока значение в ней будет больше заданного значения. Для того, чтобы найти правую границу, выберем произвольную положительную точку (например ). Будем удваивать ее до тех пор, пока значение функции в этой точке меньше заданного.
Псевдокод
double findLeftBoard(C : double):
x = -1
while f(x) > C
x = x * 2
return x
.
double findRightBoard(C : double):
x = 1
while f(x) < C
x = x * 2
return x
.
double binSearch(C : double):
left = findLeftBoard(C)
right = findRightBoard(C)
while right - left < eps // Здесь можно использовать другое условие выхода
mid = (left + right) / 2
if f(mid) < C
left = mid
else
right = mid
return (left + right) / 2
.
Метод секущих
Итерационный численный метод приближённого нахождения корня уравнения.
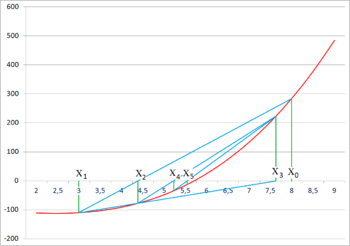
Алгоритм
Пусть нам задана монотонная и значение . Выберем две начальные точки, причем , а . Проведем через них прямую, которая пересечет прямую в точке . Теперь вместо точек и возьмем точки и , и проделаем ту же операцию и так далее, получая точки и , пока . Вычисляем каждое последующее значение с помощью формулы:
Нахождение нулей функции :
Псевдокод
double search (a : double, b : double, eps : double): // Где a — левая граница, а b — правая
while |a - b| > eps
a = b - (b - a) * f(b) / (f(b) - f(a))
b = a - (a - b) * f(a) / (f(a) - f(b))
return b
Метод Ньютона
Итерационный численный метод нахождения нуля заданной функции.
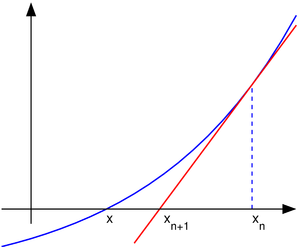
Алгоритм
Задана монотонная, дифференцируемая функция и начальное значение . Построим касательную к нашей функции в заданной точке и найдем новую точку , как пересечения касательной и оси абсцисс. Пока не выполнено заданное условие, например , вычисляем новое значение по формуле:
Псевдокод
double search (x : double, eps : double):
while f(x) > eps
x = x - f(x) / f'(x)
return x
Пример
Пусть даны числа и — число и корень какой степень нам нужно посчитать соответственно. Пусть . Возведем все выражение в -ую степень и перенесем всё в левую часть, тогда . То есть нужно найти нуль этого выражения, решим это с помощью метода Ньютона.
double nthRoot (C : double, n : double, eps : double)
while pow(x, n) - C > eps
x = x - (pow(x, n) - C) / (n * pow(x, n - 1))
return x
Замечания
- Необходимо отметить, то функция должна быть строго монотонна, если мы ищем конкретный корень и он единственный. Нестрого монотонна, если нам необходимо найти самый левый (правый) аргумент. Если же функция не монотонна, то данный алгоритм не найдет искомый аргумент, либо найдет аргумент, но он не будет единственным.
- Классической задачей на вещественный двоичный поиск является задача поиска корня -ой степени из числа : . При нижней границей для поиска будет , а верхней — .