Tango-дерево — различия между версиями
м |
м (rollbackEdits.php mass rollback) |
||
| (не показано 14 промежуточных версий 3 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Tango-дерево''' {{---}} online бинарное дерево поиска, которое изобрели Эрик Д. Демейн, Дион Хармон, Джон Яконо и | + | '''Tango-дерево''' {{---}} online бинарное дерево поиска, которое изобрели Эрик Д. Демейн, Дион Хармон, Джон Яконо и Михаи Патраску в 2004 году. |
Это лучшая известная реализация на данный момент. | Это лучшая известная реализация на данный момент. | ||
| − | Время работы tango-дерева <tex>O( | + | Время работы tango-дерева <tex>O(OPT_{dyn} \cdot \log \log n)</tex> |
==Динамическая оптимальность== | ==Динамическая оптимальность== | ||
| − | Рассмотрим для начала понятия online/offline | + | Рассмотрим для начала понятия online/offline динамически/статически оптимального дерева поиска. |
| Строка 18: | Строка 18: | ||
|definition=Пусть <tex>OPT(S)</tex> {{---}} оптимальное время работы бинарного дерева поиска для последовательности запросов <tex>S</tex>. | |definition=Пусть <tex>OPT(S)</tex> {{---}} оптимальное время работы бинарного дерева поиска для последовательности запросов <tex>S</tex>. | ||
| − | Если стоимость запросов в бинарном дереве поиска {{---}} <tex>O(n + OPT(S))</tex> для всей ключей от 1 до n, то дерево называется '''динамически оптимальным'''. Это свойство трудно показать. Неизвестно, есть ли какое-то динамически оптимальное online бинарное дерево поиска, и также неизвестно полиномиальное время для вычисления <tex>OPT(S)</tex> с точностью до константы. | + | Если стоимость запросов в бинарном дереве поиска {{---}} <tex>O(n + OPT(S))</tex> для всей ключей от <tex> 1 </tex> до <tex> n </tex>, то дерево называется '''динамически оптимальным'''. |
| + | }} | ||
| + | Это свойство трудно показать. Неизвестно, есть ли какое-то динамически оптимальное online бинарное дерево поиска, и также неизвестно полиномиальное время для вычисления <tex>OPT(S)</tex> с точностью до константы. | ||
Обозначим время работы динамически оптимального дерева <tex>O(OPT_{dyn})</tex>, где <tex>OPT_{dyn} = n + OPT(S)</tex>. | Обозначим время работы динамически оптимального дерева <tex>O(OPT_{dyn})</tex>, где <tex>OPT_{dyn} = n + OPT(S)</tex>. | ||
| − | |||
| − | |||
{{Гипотеза | {{Гипотеза | ||
| Строка 61: | Строка 61: | ||
{{Определение | {{Определение | ||
| − | |definition=Фазовая диаграмма (диаграмма состояния) работы с деревом {{---}} графическое отображение состояния дерева, при котором координата точки <tex>(x_{i}, i)</tex> означает обращение к элементу <tex>x_{i}</tex> в момент времени <tex>i</tex>. | + | |definition='''Фазовая диаграмма (диаграмма состояния) работы с деревом''' {{---}} графическое отображение состояния дерева, при котором координата точки <tex>(x_{i}, i)</tex> означает обращение к элементу <tex>x_{i}</tex> в момент времени <tex>i</tex>. |
}} | }} | ||
| Строка 153: | Строка 153: | ||
{{Определение | {{Определение | ||
| − | |definition=Числом Уилбера <tex>ch(j)</tex> называется количество смен <tex>r</tex> на <tex>l</tex> и обратно. | + | |definition='''Числом Уилбера''' <tex>ch(j)</tex> называется количество смен <tex>r</tex> на <tex>l</tex> и обратно. |
}} | }} | ||
| Строка 188: | Строка 188: | ||
{{Определение | {{Определение | ||
| − | |definition='''Жирный путь''' (англ. ''Prefered path'') {{---}} максимальный по включению путь, состоящий из | + | |definition='''Жирный путь''' (англ. ''Prefered path'') {{---}} максимальный по включению путь, состоящий из жирных ребер. |
}} | }} | ||
| Строка 198: | Строка 198: | ||
Из каждой вершины каждого splay-дерева создадим вспомогательную ссылку на корень другого splay-дерева, в котором лежит ее ребенок, связанный с ней нежирным ребром в исходном бинарном дереве поиска (при этом ссылка ставится на само дерево, а не на ребенка). | Из каждой вершины каждого splay-дерева создадим вспомогательную ссылку на корень другого splay-дерева, в котором лежит ее ребенок, связанный с ней нежирным ребром в исходном бинарном дереве поиска (при этом ссылка ставится на само дерево, а не на ребенка). | ||
| − | Корнем tango-дерева будет являться splay-дерево, которое есть жирный путь от корня исходного бинарного | + | Корнем tango-дерева будет являться splay-дерево, которое есть жирный путь от корня исходного бинарного дерева поиска. |
| Строка 222: | Строка 222: | ||
Если текущий жирный путь не содержит искомый элемент, то сделаем переход по вспомогательной ссылке (красная стрелка в tango-дереве) и осуществим поиск в новом жирном пути (splay-дереве). | Если текущий жирный путь не содержит искомый элемент, то сделаем переход по вспомогательной ссылке (красная стрелка в tango-дереве) и осуществим поиск в новом жирном пути (splay-дереве). | ||
| − | Поиск в splay-дереве (синее дерево в splay-дереве) | + | Поиск в splay-дереве (синее дерево в splay-дереве) работает за высоту от количества вершин (количество вершин {{---}} длина жирного пути (<tex>\log n</tex>)) {{---}} то есть за <tex>\log \log n</tex>. |
Поиск во всем дереве соответствует <tex>(\log \log n) \cdot </tex> число проходов по нежирному ребру. | Поиск во всем дереве соответствует <tex>(\log \log n) \cdot </tex> число проходов по нежирному ребру. | ||
| Строка 277: | Строка 277: | ||
Операции вставки и удаления в tango-дереве не поддерживаются. | Операции вставки и удаления в tango-дереве не поддерживаются. | ||
| − | == | + | ==Источники информации== |
*[http://www.lektorium.tv/lecture/14247 А.С.Станкевич, Дополнительные главы алгоритмов, Tango-деревья] | *[http://www.lektorium.tv/lecture/14247 А.С.Станкевич, Дополнительные главы алгоритмов, Tango-деревья] | ||
*[http://erikdemaine.org/theses/dharmon.pdf Dion Harmon, New Bounds on Optimal Binary Search Trees] | *[http://erikdemaine.org/theses/dharmon.pdf Dion Harmon, New Bounds on Optimal Binary Search Trees] | ||
| Строка 287: | Строка 287: | ||
[[Категория:Дискретная математика и алгоритмы]] | [[Категория:Дискретная математика и алгоритмы]] | ||
[[Категория:Деревья поиска]] | [[Категория:Деревья поиска]] | ||
| + | [[Категория:Структуры данных]] | ||
Текущая версия на 19:23, 4 сентября 2022
Tango-дерево — online бинарное дерево поиска, которое изобрели Эрик Д. Демейн, Дион Хармон, Джон Яконо и Михаи Патраску в 2004 году. Это лучшая известная реализация на данный момент.
Время работы tango-дерева
Содержание
Динамическая оптимальность
Рассмотрим для начала понятия online/offline динамически/статически оптимального дерева поиска.
В статическом бинарном дереве поиска не происходит поворотов вокруг ребер. Его оптимальность зависит только от начального положения дерева. Это отличает его от динамического дерева, в котором повороты вокруг ребер разрешены.
Offline дерево поиска получает все запросы сразу и может использовать дополнительную память и вычисления для нахождения наиболее оптимальной последовательности обработки запросов. Стоимость работы дерева поиска для заданной последовательности ключей это стоимость доступа к каждому ключу и модификации дерева, и она не зависит от того, сколько времени мы потратили, чтобы найти оптимальную последовательность.
Online дерево поиска получает следующий запрос, только когда ответит на текущий, соответственно время работы пропорциональное стоимости исполнения запросов. Таким является splay-дерево.
| Определение: |
| Пусть — оптимальное время работы бинарного дерева поиска для последовательности запросов . Если стоимость запросов в бинарном дереве поиска — для всей ключей от до , то дерево называется динамически оптимальным. |
Это свойство трудно показать. Неизвестно, есть ли какое-то динамически оптимальное online бинарное дерево поиска, и также неизвестно полиномиальное время для вычисления с точностью до константы. Обозначим время работы динамически оптимального дерева , где .
| Гипотеза: |
| Splay-деревья обладают динамической оптимальностью.
То есть если мы разрешаем перестраивать деревья в процессе запроса, то splay-деревья не больше, чем в константу хуже оптимальных. Гипотетическое время работы splay-дерева |
Модель динамически оптимального дерева
Рассмотрим ключи и запросы , где — ключ, к которому мы обращаемся.
| Утверждение: |
Существует гипотетически оптимальное дерево, которое на каждый запрос делает следующие вещи:
|
Оценка снизу на динамический оптимум
Визуализация работы с гипотетически оптимальным динамическим двоичным деревом поиска
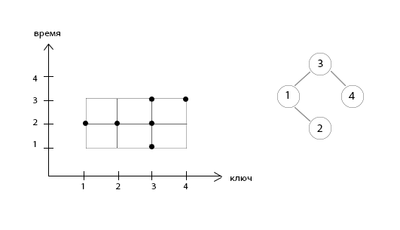
Рассмотрим систему координат ключ — время. Поставим точки, которые соответствуют обращению по данному ключу в определенное время.
Множество точек определяет, что происходило с деревом.
| Определение: |
| Множество точек называется древесным (англ. aboral), если выполняется следующее свойство: на сторонах любого невырожденного (площадь прямоугольника больше нуля) прямоугольника, построенного на двух точках, как на противоположных вершинах (левая нижняя-правая верхняя или левая верхняя-правая нижняя), есть еще хотя бы одна точка. |
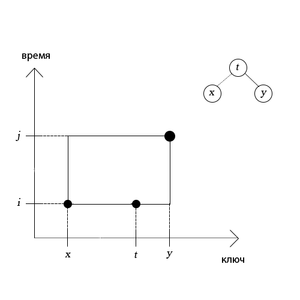
| Определение: |
| Фазовая диаграмма (диаграмма состояния) работы с деревом — графическое отображение состояния дерева, при котором координата точки означает обращение к элементу в момент времени . |
| Теорема: |
Множество точек является фазовой диаграммой работы с некоторым деревом поиска тогда и только тогда, когда оно обладает свойством древесности. |
| Доказательство: |
|
1. Фазовая диаграмма работы с деревом поиска обладает свойством древестности. Пусть мы обращались к какому-то ключу в -ом запросе и к какому-то ключу в -ом запросе. Рассмотрим этот прямоугольник. На момент -го запроса рассмотрим в дереве поиска наименьшего общего предка и — вершину . Если , то все хорошо, значит в дереве поиска она находится между и , поэтому мы к нему обращались в то время, когда шли к , значит есть точка на стороне нашего многоугольника. Если , то есть — предок в момент -го запроса, тогда рассмотрим момент -го запроса, когда мы обращались к . Найдем в дереве поиска наименьшего общего предка вершин и на момент -го запроса. Если , тогда мы к нему обращались, и есть точка на стороне нашего прямоугольника. Если , то есть — предок в момент -го запроса, Значит «всплывал», и хотя бы раз, между этими моментами выполнялся поворот вокруг ребра от к родителю. То есть во время -го запроса был в поддереве , а во время -го запроса в поддереве , значит где-то между этими моментами выполнялся поворот вокруг ребра от к родителю, и мы обращались к , следовательно есть точка на правой стороне нашего прямоугольника. 2. Если множество точек обладает свойством древесности, то оно является фазовой диаграммой работы с некоторым деревом поиска. Для любого прямоугольника, построенного на наших точках, есть еще одна точка на стороне. Докажем, что можно построить такое дерево, для которого наши точки будут соответствовать запросам. Рассмотрим наше множество точек. Построим из них декартово дерево, где ключом будет ключ, а вспомогательным ключом — время, когда мы следующий раз обратимся к вершине, то есть для каждого найдем минимальный такой, что существует точка . Приоритет будет меняться по мере того, как мы будет симулировать работу с деревом поиска. Рассмотрим общий случай Есть очередная горизонталь, на которой есть точки. Они по построению в текущий момент имеют минимальный приоритет, поэтому как-то организованы в районе корня нашего декартового дерева. Обойдем эти точки. После этого мы должны перестроить наше дерево, изменив приоритеты. Утверждается, что выполняя повороты только внутри верхней части нашего дерево можно построить дерево в соответствии с новыми приоритетами. Почему? Предположим, что это не удалось сделать. У нас есть вершина , у которой есть правый сын , и приоритет больше чем у , их надо поменять, то есть дотронуться до вершины , чего мы делать не хотели в этой строке. Но тогда рассмотрим прямоугольник (мы обращались к ). А когда-то мы обратимся к . Если есть точка на левой стороне, то к мы обратимся раньше, чем к следовательно неверно, что приоритет больше чем приоритет На левой стороне точек нет. Если на нижней стороне есть точка, значит есть точка, к которой мы обращались сейчас, ключ которой больше, чем у , но меньше , но тогда она должна быть нашим правым сыном, а не вершина . Если на правой стороне есть точка, то сейчас мы бы обращались к ней, а не к . Если на верхней стороне есть точка с ключом меньше , мы будем обращаться к ней тогда же, когда и к , значит мы может перейти к прямоугольнику, построенному на точках и . Когда таких точек (как ) не останется, то мы получим прямоугольник, у которого нет точек на всех сторонах, а это противоречит исходному условию. Поэтому при перестроении декартова дерева нам не потребуется переходить из нашей верхней зоны. |
Таким образом, мы получили какую-то offline оптимальность.
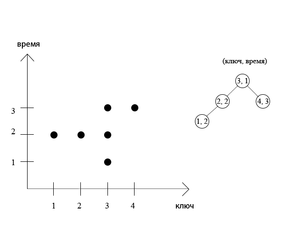
Рассмотрим наши запросы, отметим их точками, тогда время работы оптимального динамического дерева равно количество точек на диаграмме.
Получим нижнюю оценку на оптимум.
Если что-то работает за , значит это работает не более, чем в раз хуже.
Рассмотрим запросы. Покроем их независимыми прямоугольниками. Прямоугольники независимы, если угол одного не лежит внутри другого.
Можно показать, что , где — число запросов, — максимальное число независимых прямоугольников.
То есть
Вторая нижняя оценка Уилбера (Wilber)
Для каждого запроса вычислим число Уилбера.
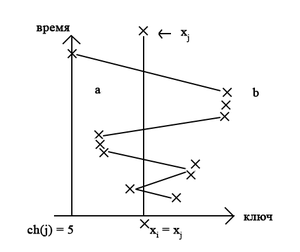
Рассмотрим запросы
Пусть , где и — левая и правая границы на момент . На момент времени . Будем передвигать левую границу каждый раз, когда встречаем число . Аналогично правую. В каждый момент времени позиция может увеличиваться, уменьшаться. Рано или поздно, наши границы и встретятся в
Напишем , если изменяется правая граница и — если левая.
| Определение: |
| Числом Уилбера называется количество смен на и обратно. |
Получаем следующую оценку
Это можно вывести из предыдущей оценки, построив соответствующее множество попарно независимых прямоугольников.
| Определение: |
| Жирное ребро (англ. Prefered edge) — ребро, соединяющее вершину с ее последним посещенным ребенком. |
| Теорема: |
Рассмотрим ключей и запросов
Организуем их в полное двоичное сбалансированное дерево. Если — не степень двойки, то на последний уровень будет заполнен не до конца. Будем в этом дереве искать наши ключи в том порядке, в котором их искали в оптимальное дереве. Для каждой вершины будем запоминать жирное ребро. Утверждается, что , где — число изменений жирных ребер. То есть если мы улучшили правую границу (мы искали что-то справа), а потом улучшили левую (искали слева от нас), значит где-то по пути мы прошли туда-обратно и сменили жирное ребро. |
Tango-деревья
Построение
Рассмотрим бинарное дерево поиска. Изначально сделаем все левые ребра жирными. Разобьем наше дерево на жирные пути.
| Определение: |
| Жирный путь (англ. Prefered path) — максимальный по включению путь, состоящий из жирных ребер. |
Каждый из этих жирных путей организуем в свое splay-дерево. Splay-дерево может быть построено как угодно.
Из каждой вершины каждого splay-дерева создадим вспомогательную ссылку на корень другого splay-дерева, в котором лежит ее ребенок, связанный с ней нежирным ребром в исходном бинарном дереве поиска (при этом ссылка ставится на само дерево, а не на ребенка).
Корнем tango-дерева будет являться splay-дерево, которое есть жирный путь от корня исходного бинарного дерева поиска.
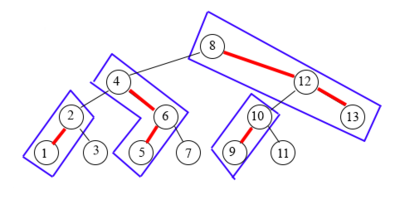
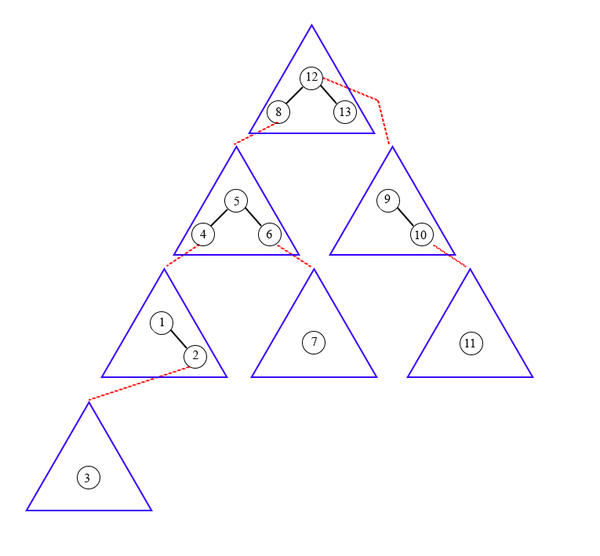
Таким образом, все наши ключи организуют иерархичную структуру — Tango-дерево.
Каждый жирный путь — splay-дерево, и каждая вершина дерева указывает на корень другого splay-дерева, в котором лежит сын вершины по нежирному ребру.
Глубина tango-дерева .
Общее время работы дерева , где — число изменений жирных ребер, — число запросов.
Операций первого становления ребра жирным — , это дает несущественный вклад в асимптотику.
Поиск
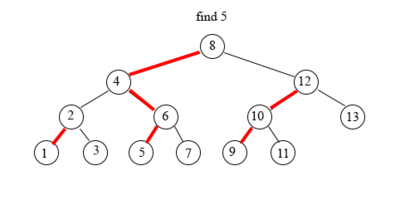
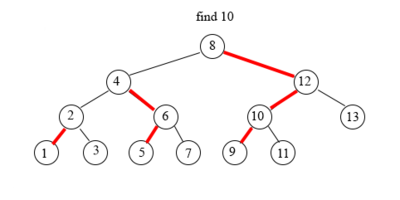
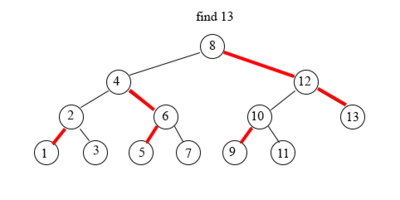
Поиск элемента в tango-дереве схож с поиском в обычном дереве поиска.
Начинаем с поиска в жирном пути корня tango-дерева — splay-дереве.
Если текущий жирный путь не содержит искомый элемент, то сделаем переход по вспомогательной ссылке (красная стрелка в tango-дереве) и осуществим поиск в новом жирном пути (splay-дереве).
Поиск в splay-дереве (синее дерево в splay-дереве) работает за высоту от количества вершин (количество вершин — длина жирного пути ()) — то есть за .
Поиск во всем дереве соответствует число проходов по нежирному ребру.
Пример
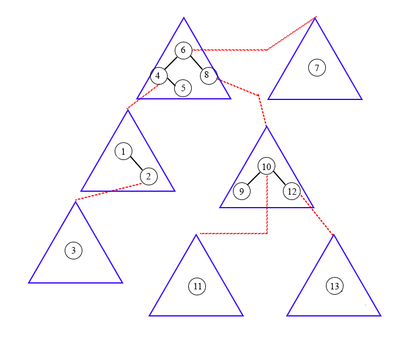
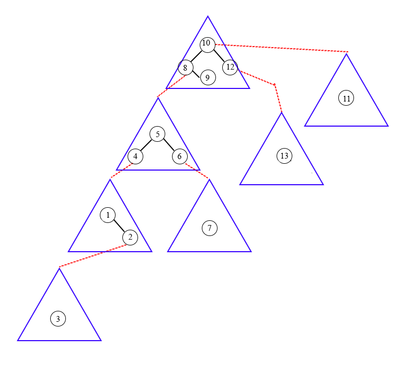
Изменение жирных ребер в бинарном дереве поиска
Соответствие tango-дерева текущему бинарному дереву поиска
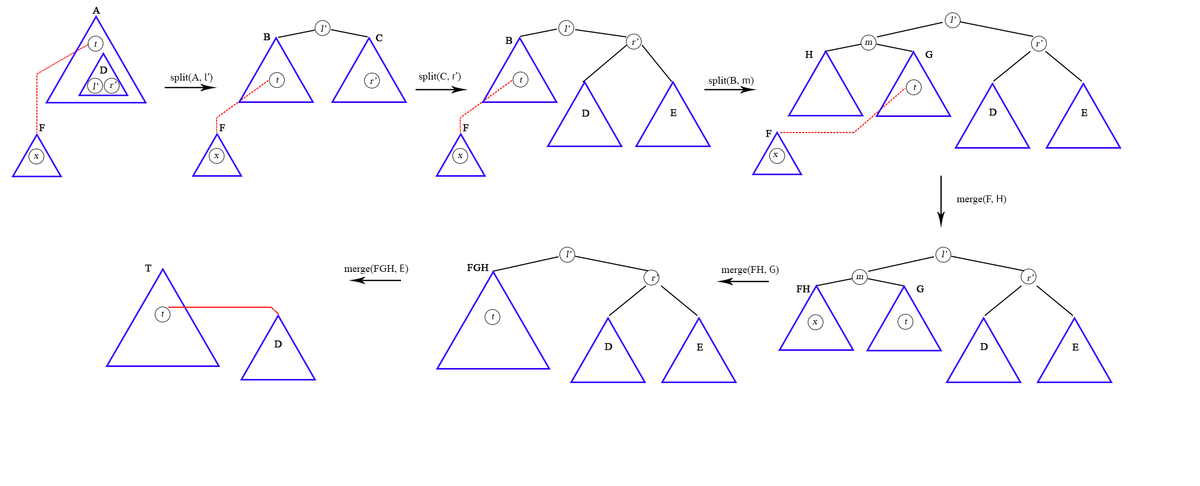
Перестройка дерева
Для того, чтобы сохранить структуру tango-дерева (splay-дерево соответствует текущему жирному пути), мы должны обновлять его каждый раз, когда жирные ребра изменяются в результате поиска. После изменения жирного ребра верхняя часть жирного пути отделяется от нижней части (которая становится самостоятельным жирным путем) и присоединяется к другому жирному пути (который становится нижней частью).
Во-первых, мы должны запомнить для каждой вершины нашего изначального дерева поиска дополнительную информацию: — минимальное значение в поддереве текущей вершины, — максимальное значение в поддереве.
Во-вторых, нам понадобятся операции split и merge, которые работают за , где — число узлов в - дереве.
Пусть для того, чтобы найти вершину , которая находится в дереве , мы прошли по тонкому ребру из вершины , находящейся в дереве . Значит, нам нужно объединить деревья и и вырезать из дерева подддерево , в которое ведет жирное ребро из вершины .
Пусть поддерево — правое. Для левого аналогично.
- Так как мы знаем интервал значений вершины в ее правом поддереве , сделаем по концам отрезка две операции . Теперь мы можем отрезать поддерево .
- Все ключи дерева меньше (так как бинарное дерево поиска), поэтому выполним операцию по максимальному значению , меньшему .
- Выполним операцию merge деревьев и .
- Выполним операцию merge деревьев и .
- Выполним операцию merge деревьев и .
- Проведем тонкое ребро от вершины к дереву .
Таким образом, перестройка = = , где — число изменений жирного ребра, — число вершин в tango-дереве.
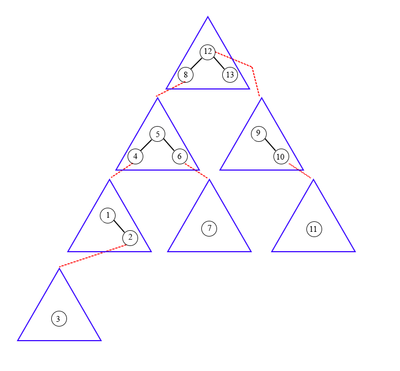
Пример
Операции вставки и удаления в tango-дереве не поддерживаются.
Источники информации
- А.С.Станкевич, Дополнительные главы алгоритмов, Tango-деревья
- Dion Harmon, New Bounds on Optimal Binary Search Trees
- Wikipedia — Tango tree
- Prof. Erik Demaine, Advanced Data Structures
- Sanjeev Arora, Competitive analysis of data structures
- Erik D. Demaine, Dion Harmon, John Iacono, Mihai Patrascu, Dynamic Optimality—Almost