Ppi1riintegerLmax — различия между версиями
Eadm (обсуждение | вклад) (Новая страница: «<tex dpi = "200"> P \mid p_i=1; r_i - integer \mid L_{max} </tex> {{Задача |definition= Дано <tex>m</tex> однородных станков, рабо...») |
м (rollbackEdits.php mass rollback) |
||
| (не показано 7 промежуточных версий 5 участников) | |||
| Строка 2: | Строка 2: | ||
{{Задача | {{Задача | ||
|definition= | |definition= | ||
| − | Дано <tex>m</tex> однородных станков, работающих параллельно, и <tex>n</tex> работ с временем выполнения <tex>p_i = 1</tex> | + | Дано <tex>m</tex> однородных станков, работающих параллельно, и <tex>n</tex> работ с временем выполнения <tex>p_i = 1</tex>, временем появления <tex>r_i</tex>, заданным целым числом, и моментом времени <tex>d_i</tex>, к которому нужно выполнить работу. Необходимо построить такое расписание, чтобы значение максимального опоздания <tex>L_{max} = \max\limits_{i=1 \ldots n} (C_i - d_i)</tex> было минимальным. |
}} | }} | ||
| + | == Описание алгоритма == | ||
| + | === Идея === | ||
| + | Отсортируем все работы по времени появления в неубывающем порядке так, что <tex>r_1 \leqslant r_2 \leqslant \ldots \leqslant r_n</tex>. Теперь будем выполнять доступные на данный момент работы в порядке неубывания дедлайнов <tex>d_i</tex>. То есть, если в момент времени <tex>t</tex> есть свободные станки и есть невыполненные работы такие, что <tex>r_i \leqslant t</tex>, то назначаем работу с наименьшим дедлайном <tex>d_i</tex> на свободный станок. | ||
| + | |||
| + | === Псевдокод === | ||
| + | Алгоритм принимает на вход массив пар, где первый элемент является временем появления <tex>r_i</tex> работы, а второй её дедлайном <tex>d_i</tex>, и возвращает расписание, представленное массивом, где на позиции <tex>i</tex> стоит момент обработки работы <tex>i</tex>. | ||
| + | |||
| + | '''function''' scheduling(jobs: '''<int, int>[n]''') -> '''int[n]''' | ||
| + | sort(jobs) <font color=green>// сортируем работы в порядке неубывания времени появления</font> | ||
| + | '''int''' j = 1 <font color=green>// последняя невыполненная работа</font> | ||
| + | '''int[n]''' ans <font color=green>// массив, куда будет записано расписание</font> | ||
| + | '''Heap<int>''' M <font color=green>// [[Двоичная куча|куча]], в которой будем хранить доступные на данный момент работы в порядке неубывания дедлайнов</font> | ||
| + | '''while''' j <= n | ||
| + | '''int''' time = jobs[j].first <font color=green>// время начала выполнения текущего блока работ</font> | ||
| + | '''while''' jobs[j].first <= time <font color=green>// добавляем в кучу все невыполненные работы, доступные на данный момент</font> | ||
| + | M.push(j) | ||
| + | j++ | ||
| + | |||
| + | '''int''' k = 0 <font color=green>// количество занятых станков в данный момент времени</font> | ||
| + | '''while''' M.notEmpty | ||
| + | i = M.pop() <font color=green>// получаем доступную работу с наименьшим дедлайном </font> | ||
| + | ans[i] = t <font color=green>// назначаем работу i на время t</font> | ||
| + | '''if''' k + 1 < m <font color=green>// если в момент t есть свободный станок, то назначаем работу i на него</font> | ||
| + | k++ | ||
| + | '''else''' <font color=green>// иначе увеличиваем время и обновляем список доступных работ</font> | ||
| + | t++ | ||
| + | k = 0 | ||
| + | '''while''' jobs[j].first <= time | ||
| + | M.push(j) | ||
| + | j++ | ||
| + | |||
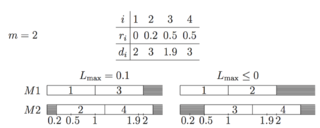
| + | [[Файл:Ppi1riintegerLmax bad.png|320px|thumb|right|Пример работы алгоритма при вещественных <tex>r_i</tex>]] | ||
| + | Внутренний цикл <tex>\mathrm{while}</tex> распределяет работы блоками, в которых они выполняются без простоя станков. После окончания такого блока, время начала выполнения следующего будет равно текущему значению <tex>r_j</tex>. | ||
| + | |||
| + | === Асимптотика === | ||
| + | Сначала мы сортируем работы, что занимает <tex> \mathcal{O}(n\log{n})</tex>. Далее идёт цикл, в котором мы <tex>n</tex> раз кладём элемент в кучу и <tex>n</tex> раз извлекаем, что также занимает <tex> \mathcal{O}(n\log{n})</tex> времени. В итоге всё вместе составляет асимптотику алгоритма <tex> \mathcal{O}(n\log{n})</tex>. | ||
| + | |||
| + | === Замечание === | ||
| + | Стоит отметить тот факт, что если снять ограничение на целочисленность <tex>r_i</tex> и позволить им принимать вещественные значения, то представленный алгоритм перестанет строить оптимальное расписание, как видно из контрпримера. | ||
| + | |||
| + | == Доказательство корректности алгоритма == | ||
| + | {{Теорема | ||
| + | |statement= | ||
| + | Приведенный алгоритм строит оптимальное расписание для задачи <tex> P \mid p_i=1; r_i - integer \mid L_{max} </tex>. | ||
| + | |proof= | ||
| + | Пусть <tex>S</tex> {{---}} расписание построенное предложенным алгоритмом, а <tex>S^*</tex> оптимальное расписание со следующими свойствами: | ||
| + | * первые <tex>r-1</tex> работ из <tex>S</tex> в обоих расписаниях назначены на одно и тоже время и | ||
| + | * значение <tex>r-1</tex> {{---}} наибольшее. | ||
| + | Таким образом работа <tex>J_r</tex> в расписании <tex>S</tex> назначена на время <tex>t</tex>, а в расписании <tex>S^*</tex> на другой более поздний момент времени. Если в момент времени <tex>t</tex> в расписании <tex>S^*</tex> есть свободный станок, то работа <tex>J_r</tex> может быть назначена на этот станок и выполнена в момент <tex>t</tex>. Иначе существует работа <tex>J_k</tex> такая, что <tex>d_r \leqslant d_k</tex>, которая выполнится в расписании <tex>S^*</tex> в момент <tex>t</tex>, а в <tex>S</tex> в другое время. Тогда мы меняем местами работы <tex>J_k</tex> и <tex>J_r</tex> в расписании <tex>S^*</tex>, что не нарушает оптимальность <tex>S^*</tex>, но является противоречием максимальности значения <tex>r-1</tex>. | ||
| + | }} | ||
| + | |||
| + | == См. также == | ||
| + | * [[Pintreepi1Lmax|<tex>P \mid intree, p_{i} = 1 \mid L_{max}</tex>]] | ||
| + | * [[PpmtnriLmax|<tex>P \mid pmtn, r_i \mid L_{max}</tex>]] | ||
| + | |||
| + | == Источники информации == | ||
| + | * Peter Brucker «Scheduling Algorithms», fifth edition, Springer {{---}} с. 111-112 ISBN 978-3-540-69515-8 | ||
| + | |||
| + | [[Категория: Алгоритмы и структуры данных]] | ||
| + | [[Категория: Теория расписаний]] | ||
Текущая версия на 19:23, 4 сентября 2022
| Задача: |
| Дано однородных станков, работающих параллельно, и работ с временем выполнения , временем появления , заданным целым числом, и моментом времени , к которому нужно выполнить работу. Необходимо построить такое расписание, чтобы значение максимального опоздания было минимальным. |
Содержание
Описание алгоритма
Идея
Отсортируем все работы по времени появления в неубывающем порядке так, что . Теперь будем выполнять доступные на данный момент работы в порядке неубывания дедлайнов . То есть, если в момент времени есть свободные станки и есть невыполненные работы такие, что , то назначаем работу с наименьшим дедлайном на свободный станок.
Псевдокод
Алгоритм принимает на вход массив пар, где первый элемент является временем появления работы, а второй её дедлайном , и возвращает расписание, представленное массивом, где на позиции стоит момент обработки работы .
function scheduling(jobs: <int, int>[n]) -> int[n]
sort(jobs) // сортируем работы в порядке неубывания времени появления
int j = 1 // последняя невыполненная работа
int[n] ans // массив, куда будет записано расписание
Heap<int> M // куча, в которой будем хранить доступные на данный момент работы в порядке неубывания дедлайнов
while j <= n
int time = jobs[j].first // время начала выполнения текущего блока работ
while jobs[j].first <= time // добавляем в кучу все невыполненные работы, доступные на данный момент
M.push(j)
j++
int k = 0 // количество занятых станков в данный момент времени
while M.notEmpty
i = M.pop() // получаем доступную работу с наименьшим дедлайном
ans[i] = t // назначаем работу i на время t
if k + 1 < m // если в момент t есть свободный станок, то назначаем работу i на него
k++
else // иначе увеличиваем время и обновляем список доступных работ
t++
k = 0
while jobs[j].first <= time
M.push(j)
j++
Внутренний цикл распределяет работы блоками, в которых они выполняются без простоя станков. После окончания такого блока, время начала выполнения следующего будет равно текущему значению .
Асимптотика
Сначала мы сортируем работы, что занимает . Далее идёт цикл, в котором мы раз кладём элемент в кучу и раз извлекаем, что также занимает времени. В итоге всё вместе составляет асимптотику алгоритма .
Замечание
Стоит отметить тот факт, что если снять ограничение на целочисленность и позволить им принимать вещественные значения, то представленный алгоритм перестанет строить оптимальное расписание, как видно из контрпримера.
Доказательство корректности алгоритма
| Теорема: |
Приведенный алгоритм строит оптимальное расписание для задачи . |
| Доказательство: |
|
Пусть — расписание построенное предложенным алгоритмом, а оптимальное расписание со следующими свойствами:
|
См. также
Источники информации
- Peter Brucker «Scheduling Algorithms», fifth edition, Springer — с. 111-112 ISBN 978-3-540-69515-8