Алгоритмы взаимного исключения — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
(Новая страница: «==Определения== {{Определение |definition= '''Взаимное исключение''' (англ. ''mutual exclusion'') — свойств…»)
 
м (rollbackEdits.php mass rollback)
 
(не показано 49 промежуточных версий 4 участников)
Строка 4: Строка 4:
 
'''Взаимное исключение''' (англ. ''mutual exclusion'') — свойство построения параллельных программ, которое используется в целях предотвращения состояния гонки (англ. ''race condition''); Оно требует, чтобы один поток исполнения никогда не входил в критическую секцию одновременно с тем, как другой параллельный поток выполнения вошел в свою критическую секцию.
 
'''Взаимное исключение''' (англ. ''mutual exclusion'') — свойство построения параллельных программ, которое используется в целях предотвращения состояния гонки (англ. ''race condition''); Оно требует, чтобы один поток исполнения никогда не входил в критическую секцию одновременно с тем, как другой параллельный поток выполнения вошел в свою критическую секцию.
 
}}
 
}}
−
 
+
То есть критические секции не могут выполняться параллельно: <tex>\forall i,j:i \neq j \Rightarrow CS_i \rightarrow CS_j \vee CS_j \rightarrow CS_i </tex>. Это значит, что выполнение критических секций будет линеаризуемо. Это требование корректности протокола взаимной блокировки.
−
То есть критические секции не могут выполняться параллельно: <tex>\forALL i,j:i\neqj \Rightarrow CS_i \rightarrow CS_j \vee CS_j \rightarrow CS_i </tex>. Это значит, что выполнение критических секций будет линеаризуемо. Это требование корректности протокола взаимной блокировки.
 
  
 
{{Определение  
 
{{Определение  
Строка 12: Строка 11:
 
}}
 
}}
  
−
Для рекуррентного соотношения, которому удовлетворяет последовательность <tex> \{ a_n \} </tex> мы часто хотим получить выражение для <tex>a_n</tex>. Например, для рекуррентного соотношения, задающего числа Фибоначчи:
+
==Проблема==
 +
Проблема, с которой связаны взаимные исключения, является проблемой совместного использования ресурсов: как можно управлять доступом нескольких процессов к общему ресурсу, когда каждый процесс нуждается в исключительном контроле над этим ресурсом при выполнении своей работы? Решение — делать доступным общий ресурс только тогда, когда процесс находится в определенном сегменте кода, называемом критической секцией. И контролировать доступ к общему ресурсу, контролируя каждое взаимное выполнение той части программы, в которой будет использоваться ресурс.
 +
 
 +
Успешное решение этой проблемы должно иметь по крайней мере три свойства:
 +
 
 +
Условие корректности:
 +
#'''Взаимное исключение''' (англ. ''mutual exclusion''): только один поток может быть в критической секции.
 +
Условия прогресса:
 +
#'''Отсутствие взаимоблокировок''' (англ. ''deadlocks''): если несколько потоков пытаются войти в критическую секцию, то хотя бы один из них должен войти в критическую секцию за конечное время.
 +
#'''Отсутствие голодания''' (англ. ''starvation-freedom''): если какой-то поток пытается войти в критическую секцию, то он войдет в критическую секцию за конечное время. Может быть последовательно усиленно, превращаясь в условие честности (англ. ''fairness'').
 +
#*Квадратичное ожидание (англ. ''quadratic wait'') — <tex>O(n^2)</tex> операций.
 +
#*Линейное ожидание (англ. ''linear wait'') — <tex>O(n)</tex> операций.
 +
#*Первый пришел, первый обслужен (англ. ''first come first served'')
 +
 
 +
 
 +
Требование <tex>First Come First Served (FCFS)</tex> формализуется так:
 +
#Метод <tex>lock</tex> должен состоять из двух последовательных секций.
 +
  '''def''' lock():
 +
      '''doorway'''
 +
      '''waiting'''
 +
#Секция <tex>doorway</tex> должны быть <tex>wait free</tex>, то есть выполняться за конечное число шагов, независимо от других потоков.
 +
#Секция <tex>waiting</tex> должна выполнять условие: Если <tex>DW_i \Rightarrow DW_j</tex>, то <tex>res(WT_i) \Rightarrow res(WT_j)</tex>.
 +
 
 +
 
 +
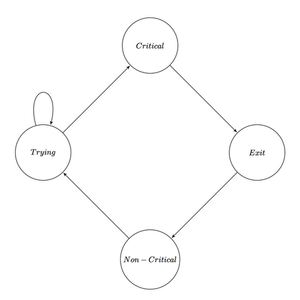
Каждая программа может быть разделена на четыре секции, что приводит к четырем состояниям. [[Файл: State_graph2.png|thumb|right|Порядок перехода между состояниями]]
 +
;Non-Critical Section: Операция находится вне критической секции; этот процесс не использует или не запрашивает общий ресурс.
 +
;Trying: Процесс пытается войти в критический раздел.
 +
;Critical Section: В этом разделе разрешен доступ к общему ресурсу.
 +
;Exit :Процесс выходит из критического раздела и делает доступный общий ресурс другим процессам.
 +
 
 +
Если процесс хочет войти в критический раздел, он должен сначала выполнить раздел <tex>try</tex> и подождать, пока он не получит доступ к критическому разделу. После того, как процесс выполнил свой критический раздел и завершился с общими ресурсами, ему необходимо выполнить раздел выхода, чтобы освободить их для использования другими процессами. Затем процесс возвращается в некритический раздел.
 +
 
 +
==Алгоритмы взаимного исключения==
 +
 
 +
===Алгоритм Петерсона для <tex>2</tex> потоков===
 +
Простейший алгоритм параллельного программирования для взаимного исключения потоков исполнения кода, разработанный Гарри Петерсоном в <tex>1981</tex> г.<ref name="original">G. L. Peterson: "Myths About the Mutual Exclusion Problem", ''Information Processing Letters'' 12(3) 1981, 115–116</ref> While Peterson's original formulation worked with only two processes, the algorithm can be generalized for more than two.</ref> Хотя изначально был сформулирован для 2-поточного случая, алгоритм может быть обобщён для произвольного количества потоков. Гарантирует взаимное исключение, отсутствие взаимной блокировки и отсутствие голодания.
 +
 
 +
Принцип работы: перед тем как начать исполнение критической секции кода, поток должен вызвать процедуру <tex>lock()</tex> со своим номером в качестве параметра. Она должна организовать ожидание потоком своей очереди входа в критическую секцию. После исполнения критической секции и выхода из неё поток вызывает другую процедуру <tex>unlock()</tex>, после чего уже другие потоки смогут войти в критическую область. Рассмотрим реализацию этого принципа алгоритмом Петерсона для двух потоков.
 +
 
 +
  '''threadlocal int''' id  <font color=green>// 0 or 1</font>
 +
  '''shared int''' want[2]
 +
  '''shared int''' victim
 +
  '''def''' lock:
 +
        want[id] = true
 +
        victim = id
 +
        '''while''' want[1-id] '''and'''
 +
              victim == id:
 +
          '''pass'''
 +
 
 +
  '''def''' unlock:
 +
    want[id] = false
 +
 
 +
===Корректность алгоритма===
 +
=====Взаимное исключение=====
 +
Потоки <tex>0</tex> и <tex>1</tex> никогда не могут попасть в критическую секцию в один момент времени: если <tex>0</tex> вошёл в секцию, он установил <tex>want[0]</tex> в <tex>true</tex>. Тогда либо <tex>want[1] = false</tex> (тогда поток <tex>1</tex> не в критической секции), либо <tex>waiting = 1</tex> (тогда поток <tex>1</tex> пытается войти в критическую секцию и крутится в цикле), либо поток <tex>1</tex> пытается войти в критическую секцию после установки <tex>want[1] = true</tex>, но до установки <tex>waiting</tex> и цикла. Таким образом, если оба процесса находятся в критической секции, должно быть <tex> want[0] \space and \space want[1] \space and \space waiting = 0 \space and \space waiting = 1 </tex>, но такого не может быть одновременно и мы пришли к противоречию.
 +
 
 +
=====Отсутствие взаимной блокировки=====
 +
Для того, чтобы оба процесса находились в ожидании, необходимы противоположные значения переменной <tex>waiting</tex>, что невозможно.
 +
=====Отсутствие голодания=====
 +
Возможна ситуация, когда один процесс будет несколько раз подряд захватывать себе критическую секцию, а другой, изъявивший желание попасть туда, будет ждать. В алгоритме Петерсона процесс не будет ждать дольше, чем один вход в критическую секцию: после выполнения <tex>unlock()</tex> и повторного захода в <tex>lock()</tex> процесс установит себя как ждущего и попадёт в цикл, который не завершится, пока не отработает другой процесс.
 +
 
 +
===Алгоритм Петерсона для <tex>N</tex> потоков===
 +
Обобщение Алгоритм Петерсона для <tex>N</tex> потоков.  Гарантирует взаимное исключение, отсутствие блокировки и отсутствие голодания. Но алгоритм не очень честный. "Невезучий" поток может ждать пока другие потоки <tex>O(N^2)</tex> раз войдут в критическую секцию (квадратичное ожидание).
 +
 
 +
  '''threadlocal int''' id  <font color=green>// 0 to N-1</font>
 +
  '''shared int''' level[N]
 +
  '''shared int''' victim[N]
 +
  '''def''' lock:
 +
    '''for''' j = 1..N-1:  <font color=green>//Для входа в CS надо пройти на N-1 уровней</font>
 +
        level[id] = j  <font color=green>//Обобщаем want на уровень j: level[id] >= j</font>
 +
        victim[j] = id  <font color=green>//Своя жертва на каждом уровне</font>
 +
        '''while''' '''exist''' k: k != id '''and'''  <font color=green>//Для прохода на следующий уровень соревнуемся со всеми другими потоками</font>
 +
              level[k] >= j '''and'''
 +
              victim[j] == id:
 +
          '''pass'''
 +
 
 +
  '''def''' unlock:
 +
    level[id] = 0
 +
 
 +
===Алгоритм Лампорта (вариант <tex>1</tex>)===
 +
Алгоритм Лампорта – алгоритм разделения общих ресурсов между несколькими потоками обладающий взаимным исключением. Опубликован Лесли Лампортом в 1974 году. <ref>[http://lamport.azurewebsites.net/pubs/bakery.pdf? A New Solution of Dijkstra's Concurrent Programming Problem]</ref> Гарантирует взаимное
 +
исключение, отсутствие блокировки и линейное ожидание.
 +
=====Аналогия=====
 +
Алгоритм реализует идею пекарни с устройством, выдающим номерки у входа. Каждому входящему покупателю выдаётся номерок на единицу больше предыдущего. Общий счётчик показывает номер обслуживаемого в данный момент клиента. Все остальные покупатели ждут, пока не закончат обслуживать текущего клиента и табло покажет следующий номер. После того как клиент сделает покупку и сдаст свой номерок, служащий увеличивает на единицу допустимые для выдачи устройством у входа номера. Если совершивший покупку клиент захочет снова что-нибудь купить, он должен будет снова взять номерок у входа и встать в общую очередь.
 +
 
 +
Пусть покупатели это потоки, получившие номера <tex>i</tex>.
 +
 
 +
=====Критическая секция=====
 +
Когда поток хочет войти в критическую секцию, он должен проверить номера <tex>n</tex>, полученные другими потоками, и убедиться, что у него меньший номер. В случае совпадения <tex>n</tex> у двух или нескольких потоков, в критическую секцию входит поток с наименьшим номером потока <tex>i</tex>.
 +
(n<sub>a</sub>, i<sub>a</sub>) < (n<sub>b</sub>, i<sub>b</sub>),
 +
что эквивалентно:
 +
(n<sub>a</sub> < n<sub>b</sub>) or ((n<sub>a</sub> == n<sub>b</sub>) and (i<sub>a</sub> < i<sub>b</sub>))
 +
Когда поток заканчивает работу в критической секции, он освобождает номер ''n'' и выходит из критической секции.
 +
 
 +
=====Псевдокод=====
 +
 
 +
  '''threadlocal int''' id  <font color=green>// 0 to N-1</font>
 +
  '''shared boolean''' want[N] '''init''' false
 +
  '''shared int''' label[N] '''init''' 0
 +
  '''def''' lock:
 +
    want[id] = true
 +
    label[id] = '''max'''(label) + 1
 +
    '''while''' '''exists''' k: k != id '''and'''
 +
          want[k] '''and'''
 +
          (label[k], k) < (label[id], id) :
 +
        '''pass'''
 +
  '''def''' unlock:
 +
    want[id] = false
  
−
<tex>
+
Обладает свойством первый пришел, первый обслужен (<tex>FCFS</tex>), за счет того, что поток <tex>P</tex> выполнивший <tex>doorway (DW)</tex> до потока <tex>Q</tex>, имеет более ранний номер в очереди. Но метки должны быть бесконечными (их можно заменить на конечные метки).
−
F_0 = 0,\qquad F_1 = 1,\qquad F_{n} = F_{n-1} + F_{n-2}, \quad n\geqslant 2, \quad n\in Z</tex>
 
  
−
<tex>a_n</tex> член может быть записан следующим образом:  <tex>a_n=\dfrac{1}{\sqrt{5}}\left( \biggl( \dfrac{1+\sqrt{5}}{2} \biggr)^n - \biggl( \dfrac{1-\sqrt{5}}{2} \biggr)^n \right).</tex>
+
=====Взаимное исключение=====
 +
Допустим, что два потока одновременно в <tex>CS</tex>. Значит поток <tex>id</tex> зашел в <tex>CS</tex> последним, в то время как другой поток <tex>k != id</tex> уже был в <tex>CS</tex>. Но зайти в <tex>CS</tex> можно если <tex>want[k] == false</tex> или <tex>(label[k], k) > (label[id], id)</tex>.
  
−
Для этого можно использовать метод производящих функций (англ. ''generating function method'').
+
'''Случай 1:''' <tex>want[k] == false</tex>
 +
*Противоречие.
  
−
==Метод производящих функций==
+
'''Случай 2:''' <tex>(label[k], k) >= (label[id], id)</tex>
−
Алгоритм получения выражения для чисел <tex>a_{n}</tex>, удовлетворяющих рекуррентному соотношению, с помощью производящих функций cостоит из <tex>4</tex> шагов.
+
*Но значит другой поток зашел по <tex>want[id] == false</tex> выполнив свой <tex>doorway</tex> до потока <tex>id</tex> - противоречие.
−
#Записать рекуррентное соотношение и начальные данные для него в следующем виде (если порядок соотношения равен <tex>k</tex>):
 
−
#:<tex>a_{0} = …, \\ a_{1} = …, \\ a_{k-1} = …, \\ … \\ a_{n} = …, n\geqslant k</tex>
 
−
#Домножить каждую строчку на <tex>z</tex> в соответствующей степени (<tex>z^{k} \cdot a_{k} = … \cdot z^{k}</tex>) и сложить все выражения, многоточие надо рассматривать как множество из выражений, где <tex>n \in [k, +\infty)</tex>. В левой части получится сумма <tex>\displaystyle\sum_{n=0}^{\infty} a_nz^n</tex> — это производящая функция, назовем ее <tex>G(z)</tex>. Правую часть преобразовать так, чтобы она превратилась в выражение, включающее <tex>G(z)</tex>.
 
−
#Решить полученное уравнение, получив для <tex>G(z)</tex> выражение в замкнутом виде.
 
−
#Разложить <tex>G(z)</tex> в степенной ряд, коэффициент при <tex>z_n</tex> будет искомым выражением для <tex>a_n</tex>.
 
  
−
==Примеры==
+
===Алгоритм Лампорта (вариант <tex>2</tex>)===
−
===<tex>1</tex> пример===
+
Еще одна реализация алгоритма Лампорта. Метки тоже могут быть бесконечными, несмотря на то, что мы их и сбрасываем при выходе из критической секции.
  
 +
  '''threadlocal int''' id  <font color=green>// 0 to N-1</font>
 +
  '''shared boolean''' want[N] '''init''' false
 +
  '''shared int''' label[N] '''init''' 0
 +
  '''def''' lock:
 +
    want[id] = true
 +
    label[id] = '''max'''(label!='''inf''') + 1
 +
    want[id] = false
 +
    '''while''' '''exists''' k: k != id '''and'''
 +
          (want[k] '''or'''
 +
          (label[k], k) < (label[id], id)) :
 +
        '''pass'''
 +
  '''def''' unlock:
 +
    label[id] = '''inf'''
  
 
==См. также==
 
==См. также==
−
* [[Производящая функция]]
+
* [[Стек_Трайбера]]
  
 
== Источники информации ==  
 
== Источники информации ==  
−
* [http://www.genfunc.ru/theory/rsol/ Решение рекуррентных соотношений]
+
* [https://en.wikipedia.org/wiki/Mutual_exclusion Mutual exclusion]
 +
* [https://en.wikipedia.org/wiki/Lamport%27s_bakery_algorithm Lamports bakery algorithm]
 +
* [http://lamport.azurewebsites.net/pubs/bakery.pdf Original lamports bakery algorithm]
 +
* [https://en.wikipedia.org/wiki/Peterson%27s_algorithm Petersons algorithm]
  
 
[[Категория: Параллельное программирование]]
 
[[Категория: Параллельное программирование]]

Текущая версия на 19:24, 4 сентября 2022

Определения

Определение:
Взаимное исключение (англ. mutual exclusion) — свойство построения параллельных программ, которое используется в целях предотвращения состояния гонки (англ. race condition); Оно требует, чтобы один поток исполнения никогда не входил в критическую секцию одновременно с тем, как другой параллельный поток выполнения вошел в свою критическую секцию.

То есть критические секции не могут выполняться параллельно: [math]\forall i,j:i \neq j \Rightarrow CS_i \rightarrow CS_j \vee CS_j \rightarrow CS_i [/math]. Это значит, что выполнение критических секций будет линеаризуемо. Это требование корректности протокола взаимной блокировки.


Определение:
Критическая секция (англ. critical section) — участок исполняемого кода программы, в котором производится доступ к общему ресурсу (данным или устройству), который не должен быть одновременно использован более чем одним потоком исполнения.


Проблема

Проблема, с которой связаны взаимные исключения, является проблемой совместного использования ресурсов: как можно управлять доступом нескольких процессов к общему ресурсу, когда каждый процесс нуждается в исключительном контроле над этим ресурсом при выполнении своей работы? Решение — делать доступным общий ресурс только тогда, когда процесс находится в определенном сегменте кода, называемом критической секцией. И контролировать доступ к общему ресурсу, контролируя каждое взаимное выполнение той части программы, в которой будет использоваться ресурс.

Успешное решение этой проблемы должно иметь по крайней мере три свойства:

Условие корректности:

  1. Взаимное исключение (англ. mutual exclusion): только один поток может быть в критической секции.

Условия прогресса:

  1. Отсутствие взаимоблокировок (англ. deadlocks): если несколько потоков пытаются войти в критическую секцию, то хотя бы один из них должен войти в критическую секцию за конечное время.
  2. Отсутствие голодания (англ. starvation-freedom): если какой-то поток пытается войти в критическую секцию, то он войдет в критическую секцию за конечное время. Может быть последовательно усиленно, превращаясь в условие честности (англ. fairness).
    • Квадратичное ожидание (англ. quadratic wait) — [math]O(n^2)[/math] операций.
    • Линейное ожидание (англ. linear wait) — [math]O(n)[/math] операций.
    • Первый пришел, первый обслужен (англ. first come first served)


Требование [math]First Come First Served (FCFS)[/math] формализуется так:

  1. Метод [math]lock[/math] должен состоять из двух последовательных секций.
  def lock():
     doorway
     waiting
  1. Секция [math]doorway[/math] должны быть [math]wait free[/math], то есть выполняться за конечное число шагов, независимо от других потоков.
  2. Секция [math]waiting[/math] должна выполнять условие: Если [math]DW_i \Rightarrow DW_j[/math], то [math]res(WT_i) \Rightarrow res(WT_j)[/math].


Каждая программа может быть разделена на четыре секции, что приводит к четырем состояниям.
Порядок перехода между состояниями
Non-Critical Section
Операция находится вне критической секции; этот процесс не использует или не запрашивает общий ресурс.
Trying
Процесс пытается войти в критический раздел.
Critical Section
В этом разделе разрешен доступ к общему ресурсу.
Exit 
Процесс выходит из критического раздела и делает доступный общий ресурс другим процессам.

Если процесс хочет войти в критический раздел, он должен сначала выполнить раздел [math]try[/math] и подождать, пока он не получит доступ к критическому разделу. После того, как процесс выполнил свой критический раздел и завершился с общими ресурсами, ему необходимо выполнить раздел выхода, чтобы освободить их для использования другими процессами. Затем процесс возвращается в некритический раздел.

Алгоритмы взаимного исключения

Алгоритм Петерсона для [math]2[/math] потоков

Простейший алгоритм параллельного программирования для взаимного исключения потоков исполнения кода, разработанный Гарри Петерсоном в [math]1981[/math] г.[1] While Peterson's original formulation worked with only two processes, the algorithm can be generalized for more than two.</ref> Хотя изначально был сформулирован для 2-поточного случая, алгоритм может быть обобщён для произвольного количества потоков. Гарантирует взаимное исключение, отсутствие взаимной блокировки и отсутствие голодания.

Принцип работы: перед тем как начать исполнение критической секции кода, поток должен вызвать процедуру [math]lock()[/math] со своим номером в качестве параметра. Она должна организовать ожидание потоком своей очереди входа в критическую секцию. После исполнения критической секции и выхода из неё поток вызывает другую процедуру [math]unlock()[/math], после чего уже другие потоки смогут войти в критическую область. Рассмотрим реализацию этого принципа алгоритмом Петерсона для двух потоков. 

  threadlocal int id  // 0 or 1
  shared int want[2]
  shared int victim
  def lock:
       want[id] = true
       victim = id
       while want[1-id] and
             victim == id:
          pass
  
  def unlock:
    want[id] = false

Корректность алгоритма

Взаимное исключение

Потоки [math]0[/math] и [math]1[/math] никогда не могут попасть в критическую секцию в один момент времени: если [math]0[/math] вошёл в секцию, он установил [math]want[0][/math] в [math]true[/math]. Тогда либо [math]want[1] = false[/math] (тогда поток [math]1[/math] не в критической секции), либо [math]waiting = 1[/math] (тогда поток [math]1[/math] пытается войти в критическую секцию и крутится в цикле), либо поток [math]1[/math] пытается войти в критическую секцию после установки [math]want[1] = true[/math], но до установки [math]waiting[/math] и цикла. Таким образом, если оба процесса находятся в критической секции, должно быть [math] want[0] \space and \space want[1] \space and \space waiting = 0 \space and \space waiting = 1 [/math], но такого не может быть одновременно и мы пришли к противоречию.

Отсутствие взаимной блокировки

Для того, чтобы оба процесса находились в ожидании, необходимы противоположные значения переменной [math]waiting[/math], что невозможно.

Отсутствие голодания

Возможна ситуация, когда один процесс будет несколько раз подряд захватывать себе критическую секцию, а другой, изъявивший желание попасть туда, будет ждать. В алгоритме Петерсона процесс не будет ждать дольше, чем один вход в критическую секцию: после выполнения [math]unlock()[/math] и повторного захода в [math]lock()[/math] процесс установит себя как ждущего и попадёт в цикл, который не завершится, пока не отработает другой процесс.

Алгоритм Петерсона для [math]N[/math] потоков

Обобщение Алгоритм Петерсона для [math]N[/math] потоков. Гарантирует взаимное исключение, отсутствие блокировки и отсутствие голодания. Но алгоритм не очень честный. "Невезучий" поток может ждать пока другие потоки [math]O(N^2)[/math] раз войдут в критическую секцию (квадратичное ожидание). 

  threadlocal int id  // 0 to N-1
  shared int level[N]
  shared int victim[N]
  def lock: 
    for j = 1..N-1:  //Для входа в CS надо пройти на N-1 уровней
       level[id] = j  //Обобщаем want на уровень j: level[id] >= j
       victim[j] = id  //Своя жертва на каждом уровне
       while exist k: k != id and  //Для прохода на следующий уровень соревнуемся со всеми другими потоками
             level[k] >= j and
             victim[j] == id:
          pass
  
  def unlock:
    level[id] = 0

Алгоритм Лампорта (вариант [math]1[/math])

Алгоритм Лампорта – алгоритм разделения общих ресурсов между несколькими потоками обладающий взаимным исключением. Опубликован Лесли Лампортом в 1974 году. [2] Гарантирует взаимное исключение, отсутствие блокировки и линейное ожидание.

Аналогия

Алгоритм реализует идею пекарни с устройством, выдающим номерки у входа. Каждому входящему покупателю выдаётся номерок на единицу больше предыдущего. Общий счётчик показывает номер обслуживаемого в данный момент клиента. Все остальные покупатели ждут, пока не закончат обслуживать текущего клиента и табло покажет следующий номер. После того как клиент сделает покупку и сдаст свой номерок, служащий увеличивает на единицу допустимые для выдачи устройством у входа номера. Если совершивший покупку клиент захочет снова что-нибудь купить, он должен будет снова взять номерок у входа и встать в общую очередь.

Пусть покупатели это потоки, получившие номера [math]i[/math].

Критическая секция

Когда поток хочет войти в критическую секцию, он должен проверить номера [math]n[/math], полученные другими потоками, и убедиться, что у него меньший номер. В случае совпадения [math]n[/math] у двух или нескольких потоков, в критическую секцию входит поток с наименьшим номером потока [math]i[/math]. 

(na, ia) < (nb, ib),

что эквивалентно: 

(na < nb) or ((na == nb) and (ia < ib))

Когда поток заканчивает работу в критической секции, он освобождает номер n и выходит из критической секции.

Псевдокод
  threadlocal int id  // 0 to N-1
  shared boolean want[N] init false
  shared int label[N] init 0
  def lock:
    want[id] = true
    label[id] = max(label) + 1
    while exists k: k != id and
          want[k] and
          (label[k], k) < (label[id], id) :
       pass
  def unlock:
    want[id] = false

Обладает свойством первый пришел, первый обслужен ([math]FCFS[/math]), за счет того, что поток [math]P[/math] выполнивший [math]doorway (DW)[/math] до потока [math]Q[/math], имеет более ранний номер в очереди. Но метки должны быть бесконечными (их можно заменить на конечные метки).

Взаимное исключение

Допустим, что два потока одновременно в [math]CS[/math]. Значит поток [math]id[/math] зашел в [math]CS[/math] последним, в то время как другой поток [math]k != id[/math] уже был в [math]CS[/math]. Но зайти в [math]CS[/math] можно если [math]want[k] == false[/math] или [math](label[k], k) \gt (label[id], id)[/math].

Случай 1: [math]want[k] == false[/math]

  • Противоречие.

Случай 2: [math](label[k], k) \gt = (label[id], id)[/math]

  • Но значит другой поток зашел по [math]want[id] == false[/math] выполнив свой [math]doorway[/math] до потока [math]id[/math] - противоречие.

Алгоритм Лампорта (вариант [math]2[/math])

Еще одна реализация алгоритма Лампорта. Метки тоже могут быть бесконечными, несмотря на то, что мы их и сбрасываем при выходе из критической секции. 

  threadlocal int id  // 0 to N-1
  shared boolean want[N] init false
  shared int label[N] init 0
  def lock:
    want[id] = true
    label[id] = max(label!=inf) + 1
    want[id] = false
    while exists k: k != id and
          (want[k] or
          (label[k], k) < (label[id], id)) :
       pass
  def unlock:
    label[id] = inf

См. также

Источники информации

  • ↑ G. L. Peterson: "Myths About the Mutual Exclusion Problem", Information Processing Letters 12(3) 1981, 115–116
  • ↑ A New Solution of Dijkstra's Concurrent Programming Problem
    • Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Алгоритмы_взаимного_исключения&oldid=85090»