Материал из Викиконспекты
|
|
| Строка 1: |
Строка 1: |
| − | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;"
| |
| − | |+
| |
| − | |-align="center"
| |
| − | |'''НЕТ ВОЙНЕ'''
| |
| − | |-style="font-size: 16px;"
| |
| − | |
| |
| − | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян.
| |
| − |
| |
| − | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием.
| |
| − |
| |
| − | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей.
| |
| − |
| |
| − | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить.
| |
| − |
| |
| − | ''Антивоенный комитет России''
| |
| − | |-style="font-size: 16px;"
| |
| − | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.
| |
| − | |-style="font-size: 16px;"
| |
| − | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки].
| |
| − | |}
| |
| − |
| |
| | {{Определение | | {{Определение |
| | |definition= | | |definition= |
Текущая версия на 19:25, 4 сентября 2022
| Определение: |
| Пусть [math]G[/math] — произвольный граф. Превратим каждое его ребро в дугу, придав ребру одно из двух возможных направлений. Полученный орграф на том же самом множестве вершин будем называть ориентацией графа [math]G[/math]. |
| Лемма: |
|
| Доказательство: |
| [math]\triangleright[/math] |
|
При умножении [math]i[/math]-й строки исходной матрицы [math]I[/math] на [math]j[/math]-й столбец транспонированной матрицы [math]I^T [/math] перемножаются [math]i[/math]-я и [math]j[/math]-я строки исходной матрицы. При умножении [math]i[/math]-й строки на саму себя на диагонали полученной матрицы получится сумма квадратов элементов [math]i[/math]-й строки, которая равна, очевидно, [math]\deg(v_i)[/math]. Пусть теперь [math]i \ne j[/math]. Если [math] (v_i, v_j) \in E [/math], то существует ровно одно ребро, соединяющее [math] v_i [/math] и [math] v_j [/math], следовательно результат перемножения [math]i[/math]-й и [math]j[/math]-й строк равен [math]-1[/math], в противном случае он равен [math]0[/math] в силу отсутствия ребра, инцидентного обеим вершинам. Определенная данными условиями матрица и является матрицей Кирхгофа. |
| [math]\triangleleft[/math] |
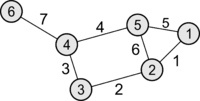
| Граф
|
Матрица Кирхгофа
|
Матрица инцидентности
|
|
[math]\left(\begin{array}{rrrrrr}
2 & -1 & 0 & 0 & -1 & 0\\
-1 & 3 & -1 & 0 & -1 & 0\\
0 & -1 & 2 & -1 & 0 & 0\\
0 & 0 & -1 & 3 & -1 & -1\\
-1 & -1 & 0 & -1 & 3 & 0\\
0 & 0 & 0 & -1 & 0 & 1\\
\end{array}\right)[/math]
|
[math]\begin{pmatrix}
1 & 0 & 0 & 0 & 1 & 0 & 0\\
1 & 1 & 0 & 0 & 0 & 1 & 0\\
0 & 1 & 1 & 0 & 0 & 0 & 0\\
0 & 0 & 1 & 1 & 0 & 0 & 1\\
0 & 0 & 0 & 1 & 1 & 1 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 1\\
\end{pmatrix}[/math]
|
См. также
Источники информации
- Асанов М., Баранский В., Расин В. — Дискретная математика: Графы, матроиды, алгоритмы — Ижевск: ННЦ "Регулярная и хаотическая динамика", 2001, 288 стр.
