Примеры сведения к задачам поиска потока — различия между версиями
Sultazat (обсуждение | вклад) м (→Источники) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 26 промежуточных версий 8 участников) | |||
| Строка 1: | Строка 1: | ||
Рассмотрим несколько задач, которые решаются путём сведения к задаче о поиске максимального потока в сети. | Рассмотрим несколько задач, которые решаются путём сведения к задаче о поиске максимального потока в сети. | ||
| − | == Лабиринт Минотавра == | + | == Пример №1. Лабиринт Минотавра == |
{{Задача | {{Задача | ||
|definition = Дано поле размером <tex>N \times M</tex>, некоторые клетки поля закрашены. В одной из незакрашенных клеток поля стоит Минотавр, он умеет ходить только по незакрашенным клеткам (из текущей клетки он может пойти только в ту клетку, с которой имеет общую сторону). Какое минимальное количество клеток нужно закрасить, чтобы Минотавр не смог выбраться за пределы поля? | |definition = Дано поле размером <tex>N \times M</tex>, некоторые клетки поля закрашены. В одной из незакрашенных клеток поля стоит Минотавр, он умеет ходить только по незакрашенным клеткам (из текущей клетки он может пойти только в ту клетку, с которой имеет общую сторону). Какое минимальное количество клеток нужно закрасить, чтобы Минотавр не смог выбраться за пределы поля? | ||
}} | }} | ||
| − | |||
<includeonly>{{#if: {{{neat|}}}| | <includeonly>{{#if: {{{neat|}}}| | ||
<div style="background-color: #fcfcfc; float:left;"> | <div style="background-color: #fcfcfc; float:left;"> | ||
| Строка 16: | Строка 15: | ||
</table>}} | </table>}} | ||
</includeonly> | </includeonly> | ||
| − | [[Файл:Monster.png | + | [[Файл:Monster.png|Пример поля]] [[Файл:MonsterSolution.png|Решение текущего примера]] |
| + | |||
Сразу скажем, что выбраться за пределы поля эквивалентно тому, что Минотавр может дойти до какой-либо крайней клетки. | Сразу скажем, что выбраться за пределы поля эквивалентно тому, что Минотавр может дойти до какой-либо крайней клетки. | ||
| − | + | === Решение и доказательство корректности === | |
| + | |||
| + | {{Теорема | ||
| + | |statement= | ||
| + | Минимальное количество клеток, которое нужно закрасить, равно максимальному количеству клеточно-непересекающихся путей из позиции Минотавра до крайних клеток поля. | ||
| + | |proof= | ||
| + | Очевидно, что ответ не больше, чем количество всех путей от Минотавра до крайних клеток. Сделаем ещё более строгое неравенство: ответ не больше, чем максимальное количество клеточно-непересекающихся путей, т.к. если взять какие-нибудь <tex>2</tex> пересекающихся пути и закрасить клетку в позиции, где они пересекаются, то блокируется выход за пределы поля сразу по <tex>2</tex> этим путям. С другой стороны, если закрасить клетку на каком-то из путей, то блокируется только этот путь, т.к. были взяты клеточно-непересекающиеся пути. Значит, ответ не меньше, чем количество таких путей. | ||
| + | }} | ||
| + | |||
| + | === Переход к сети === | ||
| − | Рассмотрим [[Определение сети, потока#flow_network|сеть]], в которой вершинам будут соответствовать незакрашенные клетки поля, соседние незакрашенные клетки соединим ориентированными рёбрами с пропускной способностью 1. В качестве истока возьмём вершину, которой соответствует клетка Минотавр. Добавим в граф ещё одну вершину — сток, добавим рёбра из вершин, соответствующим крайним клеткам поля, в сток с пропускной способностью 1. Чтобы пути не пересекались по клеткам, раздвоим каждую вершину графа на 2 вершины: в одну будут только входить рёбра, из другой — только выходить рёбра, и сами эти вершины соединим ребром с пропускной способностью 1. | + | Рассмотрим [[Определение сети, потока#flow_network|сеть]], в которой вершинам будут соответствовать незакрашенные клетки поля, соседние незакрашенные клетки соединим ориентированными рёбрами с пропускной способностью <tex>1</tex>. В качестве истока возьмём вершину, которой соответствует клетка Минотавр. Добавим в граф ещё одну вершину — сток, добавим рёбра из вершин, соответствующим крайним клеткам поля, в сток с пропускной способностью <tex>1</tex>. Чтобы пути не пересекались по клеткам, раздвоим каждую вершину графа на <tex>2</tex> вершины: в одну будут только входить рёбра, из другой — только выходить рёбра, и сами эти вершины соединим ребром с пропускной способностью <tex>1</tex>. |
[[Файл:Dublicate2.png|center]] | [[Файл:Dublicate2.png|center]] | ||
| Строка 27: | Строка 36: | ||
Используя [[Алгоритм Форда-Фалкерсона, реализация с помощью поиска в глубину|алгоритм Форда-Фалкерсона]], найдём максимальный поток в сети. Согласно [[Теорема о декомпозиции|теореме о декомпозиции]], нахождение максимального потока эквивалентно тому, что мы нашли максимальное количество путей из истока в сток. Т.е. требуемый ответ на задачу равен максимальному потоку. | Используя [[Алгоритм Форда-Фалкерсона, реализация с помощью поиска в глубину|алгоритм Форда-Фалкерсона]], найдём максимальный поток в сети. Согласно [[Теорема о декомпозиции|теореме о декомпозиции]], нахождение максимального потока эквивалентно тому, что мы нашли максимальное количество путей из истока в сток. Т.е. требуемый ответ на задачу равен максимальному потоку. | ||
| − | Время работы алгоритма Форда-Фалкерсона <tex>O(E|f|)</tex>. Первое замечание: <tex>E</tex> <tex>\leqslant</tex> <tex>4V</tex> <tex>\leqslant</tex> <tex>4NM</tex> (это следует из того, что из каждой вершины исходит не более 4 рёбер), т.е. <tex>E=O(NM)</tex>. Второе замечание: ответ не превосходит 4, т.к. можно закрасить клетку слева, справа, сверху и снизу от позиции Минотавра и он не сможет никуда двигаться, поэтому <tex>|f|</tex> можно считать константой. Итоговое время работы <tex>O(NM)</tex>. | + | === Оценка времени работы === |
| + | |||
| + | Время работы алгоритма Форда-Фалкерсона <tex>O(E|f|)</tex>. Первое замечание: <tex>E</tex> <tex>\leqslant</tex> <tex>4V</tex> <tex>\leqslant</tex> <tex>4NM</tex> (это следует из того, что из каждой вершины исходит не более <tex>4</tex> рёбер), т.е. <tex>E=O(NM)</tex>. Второе замечание: ответ не превосходит <tex>4</tex>, т.к. можно закрасить клетку слева, справа, сверху и снизу от позиции Минотавра и он не сможет никуда двигаться, поэтому <tex>|f|</tex> можно считать константой. Итоговое время работы <tex>O(NM)</tex>. | ||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Задача о максимальном потоке ]] | [[Категория: Задача о максимальном потоке ]] | ||
| + | |||
| + | ==Пример №2. Испорченный паркет.== | ||
| + | {{Задача | ||
| + | |definition = Дан паркет размером <tex>N \times M</tex>, некоторые клетки которого испорчены, их необходимо закрыть новыми плитками. Плитки бывают размером <tex>2 \times 1</tex> ценой <tex>A</tex>, и <tex>1 \times 1</tex> ценой <tex>B</tex>. Плитки можно поворачивать, но нельзя разрезать. Какую минимальную сумму нужно потратить, чтобы заложить испорченные плитки паркета. Новые плитки не должны перекрывать никакие другие плитки. | ||
| + | }} | ||
| + | ===Решение=== | ||
| + | {| cellpadding="3" style="margin-left: auto; margin-right: auto;" | ||
| + | | [[Файл:Parquet_example_1.png|thumb|400px|Пример паркета]] | ||
| + | | [[Файл:Parquet_example_2.png|thumb|400px|Пример раскраски]] | ||
| + | |} | ||
| + | Сначала проверим, что <tex>2 \times B>A</tex>. Если это условие не выполнено, то все выгодней замостить только плитками <tex>1 \times 1</tex> и больше нечего считать. Теперь на нужно максимизировать количество плиток ценой <tex>A</tex>. | ||
| + | Раскрасим наш паркет по принципу шахматной доски, тогда один конец плитки <tex>2 \times 1</tex> будет лежать на черной клетке, другой – на белой. Итак, построим двудольный граф, одна доля которого будет содержать белые клетки, другая – черные. Ребра весом в <tex>1</tex> проведем между граничащими клетками. Добавим исток с ребрами в белые вершины весом в 1 и сток с ребрами из черных клеток весом тоже в 1. Пускай <tex>f</tex> – величина найденного максимального потока между истоком и стоком, это и будет количество плиток <tex>2 \times 1</tex>. Ответом к задаче будет величина <tex>f \times A+(K-f) \times B</tex>, где <tex>K</tex> – общее число испорченных клеток. | ||
| + | |||
| + | ===Доказательство корректности=== | ||
| + | Заметим следующее: мы ищем максимальное паросочетание в двудольном графе. Это означает, что белая вершина будет соединена не более чем с одной чёрной и наоборот – это именно то, что нам нужно, ведь соединяя чёрную клетку с белой, мы понимаем, что можем разместить здесь плитку размером <tex>2 \times 1</tex> и она не будет ни с чем пересекаться. Теперь мы ищем максимальное число таких рёбер. Это всё происходит также, как и в сведении задачи поиска максимального паросочетания к задаче о нахождении максимального потока. | ||
| + | === Оценка времени работы === | ||
| + | |||
| + | Величину максимального потока можно искать с помощью алгоритма Форда-Фалкерсона, его время работы <tex>O(E|f|)</tex>, где <tex>|f|</tex> – величина найденного максимального потока. Заметим, что <tex>|f| \leqslant \dfrac K 2</tex>, где <tex>K</tex> – общее число испорченных клеток. Также заметим, что <tex>E \leqslant K \times 4</tex>, т.к. <tex>K</tex> рёбер исходят из истока и входят в сток и максимум <tex>4</tex> ребра могут исходить из вершины в левой доле в правую. Из всего этого следует, что итоговое время работы будет <tex>O(K^2)</tex> | ||
| + | |||
| + | ==Пример №3. Коллекционер монет.== | ||
| + | {{Задача | ||
| + | |definition=Есть <tex>N</tex> коллекционеров и <tex>M</tex> видов монет. Для вступления в клуб, необходимо иметь не меньше одной монеты каждого типа. Вы (у вас номер 1) можете меняться с коллекционерами имеющимися монетами. Любой коллекционер обменяет свою монету <tex>a</tex> на вашу монету <tex>b</tex>, если у него '''больше''' одной монеты типа <tex>a</tex> и нету ни одной монеты типа <tex>b</tex>. Вы, в свою очередь, можете нарушать это правило. Нужно набрать как можно больше типов монет по известной ситуации у всех коллекционеров. | ||
| + | }} | ||
| + | ===Решение=== | ||
| + | [[Файл:Coints_task.gif|400px|thumb|right|Жёлтые вершины – монеты разных типов, синие – коллекционеры. Красное ребро означает, что коллекционеру нужна монета этого типа, причём пропускная способнасть этого ребра равна 1, зелёное – что у него больше одной монеты данного типа]] | ||
| + | Построим сеть следующего вида: создадим для каждого типа монет по одной вершине, эти вершины будут соответствовать вашим монетам. Нужно собрать как можно больше уникальных монет, поэтому проведем ребро пропускной способности <tex>1</tex> в сток из каждой такой вершины. В вершины, соответствующие монетам, которые у Вас есть изначально, проведем ребро, пропускная способность которого равна количеству таких монет у вас. Для каждого члена клуба (кроме вас) заведем по одной вершине. Эта вершина может принимать не более одной монеты, которой у него нет и отдавать не более <tex>k-1</tex> монеты, которых у него <tex>k</tex> <tex>(k > 1)</tex>. Естественно, член клуба отдает одну монету взамен одной полученной. Таким образом, в каждую такую вершину нужно провести ребро пропускной способности <tex>1</tex> из вершин соответствующих монетам, которых нет у этого члена клуба. А из этих вершин нужно провести ребра пропускной способностью <tex>k_i - 1</tex> в вершину <tex>i</tex>, соответствующую монетам, которых у члена клуба больше одной. Построенная сеть отражает процессы обмена в клубе. Максимальный поток в такой сети будет равен максимальному количеству монет, которые могуть быть собраны вами. | ||
| + | ===Доказательство корректности=== | ||
| + | Как уже было сказано, построенная сеть отражает процессы обмена в клубе, пример можно посмотреть на картинке выше. Заметим следующее: | ||
| + | * из вершины каждого типа монет может выйти поток, величина которого <tex>\leqslant 1 </tex> | ||
| + | * в вершины каждого типа монет может войти поток, величина которого не больше количества монет данного типа | ||
| + | * если коллекционеру нужна эта монета и мы решили дать её, то мы дадим максимум одну монету этого типа, т.к. пропускная способность красного ребра <tex>= 1</tex>. | ||
| + | * если в данную вершину пришёл поток данной величины, то мы должны отдать из этой вершины поток такой же величины. (Из определения потока) | ||
| + | Всё вышесказанное подтверждает то, что построенная сеть корректно отображает процессы обмена монетами между участниками. | ||
| + | === Оценка времени работы === | ||
| + | |||
| + | Величину максимального потока можно искать с помощью алгоритма Форда-Фалкерсона, его время работы <tex>O(E|f|)</tex>, где <tex>|f|</tex> – величина найденного максимального потока. Заметим, что <tex>|f| \leqslant M</tex>, где <tex>M</tex> – количество типов монет. Также заметим, что <tex>E = M \times 2 + E^*</tex>, где <tex>E^*</tex> – общее минимальное число монет, которые нужно получить все коллекционерам (кроме вас), чтобы вступить в клуб <tex>+</tex> сумма типов монет, которых больше <tex>1</tex>, по всем коллекционерам. Из всего этого следует, что итоговое время работы будет <tex>O(ME)</tex> | ||
== См.также == | == См.также == | ||
* [[Схема алгоритма Диница]] | * [[Схема алгоритма Диница]] | ||
| + | * [[Алгоритм Форда-Фалкерсона, реализация с помощью поиска в глубину]] | ||
| + | * [[Алгоритм масштабирования потока]] | ||
| − | == Источники == | + | == Источники информации == |
* [https://icpc.baylor.edu/regionals/finder/west-siberian-subregional-2016 The 2016 West Siberian Subregional Contest] | * [https://icpc.baylor.edu/regionals/finder/west-siberian-subregional-2016 The 2016 West Siberian Subregional Contest] | ||
| + | * [https://www.dropbox.com/s/o24szu3mj341wig/WPS2009.pdf?dl=0 Зимняя школа по программированию, Харьков 2009 ] | ||
| + | * [http://codeforces.com/blog/entry/19068?locale=ru Codeforces лекции Зимней Школы по Программированию] | ||
Текущая версия на 19:26, 4 сентября 2022
Рассмотрим несколько задач, которые решаются путём сведения к задаче о поиске максимального потока в сети.
Содержание
Пример №1. Лабиринт Минотавра
| Задача: |
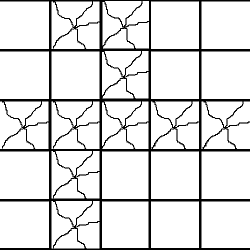
| Дано поле размером , некоторые клетки поля закрашены. В одной из незакрашенных клеток поля стоит Минотавр, он умеет ходить только по незакрашенным клеткам (из текущей клетки он может пойти только в ту клетку, с которой имеет общую сторону). Какое минимальное количество клеток нужно закрасить, чтобы Минотавр не смог выбраться за пределы поля? |
Сразу скажем, что выбраться за пределы поля эквивалентно тому, что Минотавр может дойти до какой-либо крайней клетки.
Решение и доказательство корректности
| Теорема: |
Минимальное количество клеток, которое нужно закрасить, равно максимальному количеству клеточно-непересекающихся путей из позиции Минотавра до крайних клеток поля. |
| Доказательство: |
| Очевидно, что ответ не больше, чем количество всех путей от Минотавра до крайних клеток. Сделаем ещё более строгое неравенство: ответ не больше, чем максимальное количество клеточно-непересекающихся путей, т.к. если взять какие-нибудь пересекающихся пути и закрасить клетку в позиции, где они пересекаются, то блокируется выход за пределы поля сразу по этим путям. С другой стороны, если закрасить клетку на каком-то из путей, то блокируется только этот путь, т.к. были взяты клеточно-непересекающиеся пути. Значит, ответ не меньше, чем количество таких путей. |
Переход к сети
Рассмотрим сеть, в которой вершинам будут соответствовать незакрашенные клетки поля, соседние незакрашенные клетки соединим ориентированными рёбрами с пропускной способностью . В качестве истока возьмём вершину, которой соответствует клетка Минотавр. Добавим в граф ещё одну вершину — сток, добавим рёбра из вершин, соответствующим крайним клеткам поля, в сток с пропускной способностью . Чтобы пути не пересекались по клеткам, раздвоим каждую вершину графа на вершины: в одну будут только входить рёбра, из другой — только выходить рёбра, и сами эти вершины соединим ребром с пропускной способностью .
Используя алгоритм Форда-Фалкерсона, найдём максимальный поток в сети. Согласно теореме о декомпозиции, нахождение максимального потока эквивалентно тому, что мы нашли максимальное количество путей из истока в сток. Т.е. требуемый ответ на задачу равен максимальному потоку.
Оценка времени работы
Время работы алгоритма Форда-Фалкерсона . Первое замечание: (это следует из того, что из каждой вершины исходит не более рёбер), т.е. . Второе замечание: ответ не превосходит , т.к. можно закрасить клетку слева, справа, сверху и снизу от позиции Минотавра и он не сможет никуда двигаться, поэтому можно считать константой. Итоговое время работы .
Пример №2. Испорченный паркет.
| Задача: |
| Дан паркет размером , некоторые клетки которого испорчены, их необходимо закрыть новыми плитками. Плитки бывают размером ценой , и ценой . Плитки можно поворачивать, но нельзя разрезать. Какую минимальную сумму нужно потратить, чтобы заложить испорченные плитки паркета. Новые плитки не должны перекрывать никакие другие плитки. |
Решение
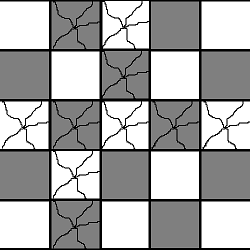
Сначала проверим, что . Если это условие не выполнено, то все выгодней замостить только плитками и больше нечего считать. Теперь на нужно максимизировать количество плиток ценой . Раскрасим наш паркет по принципу шахматной доски, тогда один конец плитки будет лежать на черной клетке, другой – на белой. Итак, построим двудольный граф, одна доля которого будет содержать белые клетки, другая – черные. Ребра весом в проведем между граничащими клетками. Добавим исток с ребрами в белые вершины весом в 1 и сток с ребрами из черных клеток весом тоже в 1. Пускай – величина найденного максимального потока между истоком и стоком, это и будет количество плиток . Ответом к задаче будет величина , где – общее число испорченных клеток.
Доказательство корректности
Заметим следующее: мы ищем максимальное паросочетание в двудольном графе. Это означает, что белая вершина будет соединена не более чем с одной чёрной и наоборот – это именно то, что нам нужно, ведь соединяя чёрную клетку с белой, мы понимаем, что можем разместить здесь плитку размером и она не будет ни с чем пересекаться. Теперь мы ищем максимальное число таких рёбер. Это всё происходит также, как и в сведении задачи поиска максимального паросочетания к задаче о нахождении максимального потока.
Оценка времени работы
Величину максимального потока можно искать с помощью алгоритма Форда-Фалкерсона, его время работы , где – величина найденного максимального потока. Заметим, что , где – общее число испорченных клеток. Также заметим, что , т.к. рёбер исходят из истока и входят в сток и максимум ребра могут исходить из вершины в левой доле в правую. Из всего этого следует, что итоговое время работы будет
Пример №3. Коллекционер монет.
| Задача: |
| Есть коллекционеров и видов монет. Для вступления в клуб, необходимо иметь не меньше одной монеты каждого типа. Вы (у вас номер 1) можете меняться с коллекционерами имеющимися монетами. Любой коллекционер обменяет свою монету на вашу монету , если у него больше одной монеты типа и нету ни одной монеты типа . Вы, в свою очередь, можете нарушать это правило. Нужно набрать как можно больше типов монет по известной ситуации у всех коллекционеров. |
Решение
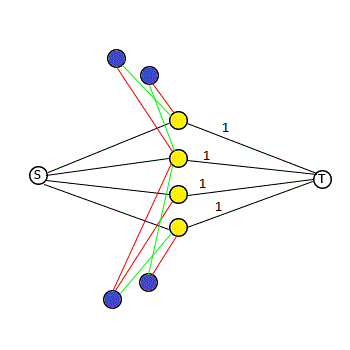
Построим сеть следующего вида: создадим для каждого типа монет по одной вершине, эти вершины будут соответствовать вашим монетам. Нужно собрать как можно больше уникальных монет, поэтому проведем ребро пропускной способности в сток из каждой такой вершины. В вершины, соответствующие монетам, которые у Вас есть изначально, проведем ребро, пропускная способность которого равна количеству таких монет у вас. Для каждого члена клуба (кроме вас) заведем по одной вершине. Эта вершина может принимать не более одной монеты, которой у него нет и отдавать не более монеты, которых у него . Естественно, член клуба отдает одну монету взамен одной полученной. Таким образом, в каждую такую вершину нужно провести ребро пропускной способности из вершин соответствующих монетам, которых нет у этого члена клуба. А из этих вершин нужно провести ребра пропускной способностью в вершину , соответствующую монетам, которых у члена клуба больше одной. Построенная сеть отражает процессы обмена в клубе. Максимальный поток в такой сети будет равен максимальному количеству монет, которые могуть быть собраны вами.
Доказательство корректности
Как уже было сказано, построенная сеть отражает процессы обмена в клубе, пример можно посмотреть на картинке выше. Заметим следующее:
- из вершины каждого типа монет может выйти поток, величина которого
- в вершины каждого типа монет может войти поток, величина которого не больше количества монет данного типа
- если коллекционеру нужна эта монета и мы решили дать её, то мы дадим максимум одну монету этого типа, т.к. пропускная способность красного ребра .
- если в данную вершину пришёл поток данной величины, то мы должны отдать из этой вершины поток такой же величины. (Из определения потока)
Всё вышесказанное подтверждает то, что построенная сеть корректно отображает процессы обмена монетами между участниками.
Оценка времени работы
Величину максимального потока можно искать с помощью алгоритма Форда-Фалкерсона, его время работы , где – величина найденного максимального потока. Заметим, что , где – количество типов монет. Также заметим, что , где – общее минимальное число монет, которые нужно получить все коллекционерам (кроме вас), чтобы вступить в клуб сумма типов монет, которых больше , по всем коллекционерам. Из всего этого следует, что итоговое время работы будет
См.также
- Схема алгоритма Диница
- Алгоритм Форда-Фалкерсона, реализация с помощью поиска в глубину
- Алгоритм масштабирования потока