F2Cmax — различия между версиями
GR1n (обсуждение | вклад) (→Доказательство корректности алгоритма) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 33 промежуточные версии 5 участников) | |||
| Строка 1: | Строка 1: | ||
| − | == | + | <tex dpi=200>F2 \mid\mid C_{max} </tex> |
| − | Рассмотрим задачу: | + | {{Задача |
| − | + | |definition=Рассмотрим задачу: | |
| − | + | *дано <tex>n</tex> работ и <tex>2</tex> станка, | |
| − | + | *для каждой работы известно её время выполнения на каждом станке <tex>p_{ij}</tex>, | |
| − | + | *каждую работу необходимо выполнить сначала на первом станке, а потом на втором. | |
| − | + | Требуется минимизировать время окончания выполнения всех работ. }} | |
| − | Требуется минимизировать время окончания всех работ. | + | |
== Описание алгоритма == | == Описание алгоритма == | ||
Пусть <tex>p_{i1}</tex> {{---}} время выполнения <tex>i</tex>-ой работы на первом станке, а <tex>p_{i2}</tex> {{---}} на втором.<br/> | Пусть <tex>p_{i1}</tex> {{---}} время выполнения <tex>i</tex>-ой работы на первом станке, а <tex>p_{i2}</tex> {{---}} на втором.<br/> | ||
<ol> | <ol> | ||
| − | <li> | + | <li>Алгоритм строит два списка <tex> L </tex> и <tex> R </tex>. Изначально они пусты. Также поддерживается множество еще не распределенных по спискам <tex> L </tex> и <tex> R </tex> работ <tex>X = \{i \mid i = 1, \dots, n\}</tex> </li> |
| − | <li> Пока множество <tex> X </tex> | + | <li> Пока множество <tex> X </tex> не пусто, распределяем работы по спискам следующим образом: |
<ul> | <ul> | ||
| − | <li> | + | <li> находим такие индексы <tex> i </tex> и <tex> j </tex>, что <tex>p_{ij} = \min \{ p_{ij} \mid i \in X \land j = 1, 2\}</tex>, </li> |
| − | <li> | + | <li>если минимум достигается на первом станке (иными словами <tex> j = 1 </tex>), то поставим работу <tex> i </tex> в конец списка <tex> L </tex>, иначе ставим в начало списка <tex> R </tex>, </li> |
| − | <li> | + | <li>удаляем работу <tex> i </tex> из множества <tex> X </tex>. </li> |
</ul> | </ul> | ||
</li> | </li> | ||
| − | <li> Рассмотрим | + | <li> Рассмотрим список <tex> T = L ~\texttt{++}~ R</tex> {{---}} конкатенацию <tex> L</tex> и <tex>R</tex>. Утверждается, что этот список является оптимальной перестановкой работ как на первом, так и на втором станке. Далее расставляем подряд работы на первом станке согласно перестановке, после чего ставим в том же порядке работы на втором станке, при этом избегая одновременного выполнения одной и той же работы. </li> |
</ol> | </ol> | ||
==Доказательство корректности алгоритма== | ==Доказательство корректности алгоритма== | ||
| − | + | {{ | |
| + | Теорема|statement= | ||
| + | Существует оптимальное расписание, в котором станки выполняют работы в одном и том же порядке. | ||
| + | |||
| + | |proof= | ||
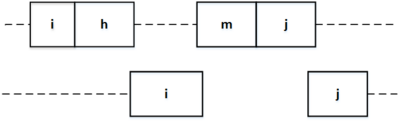
| + | [[Файл:f2cmax_first_fixed.png|400px|thumb|right|Рис. 1]] | ||
| + | Предположим обратное: что не существует оптимального расписания с одинаковыми перестановками работ на станках. | ||
| + | Рассмотрим некоторое оптимальное расписание с максимальным по длине общим префиксом на станках. Пусть его длина равна <tex> k </tex>, где <tex> k < n </tex>. Пусть на <tex> k </tex> позиции на первом и втором станках стоит работа <tex> i </tex>, а на втором станке на позиции <tex> k + 1 </tex> стоит работа <tex> j </tex>. Тогда заметим, что если мы поставим работу <tex> j </tex> на первом станке сразу после работы <tex> i </tex>, то последовательные работы с <tex> h </tex> по <tex> m </tex> (см. рис. 1) по-прежнему будут успевать выполниться, так как на втором станке они выполняются в текущем расписании после <tex> j </tex>. Таким образом нам удалось увеличить длину наибольшего общего префикса, а так как по нашему предположению она была максимальна, то предположение неверно и искомое расписание с одинаковым порядком выполнения работ на обоих станках существует. | ||
| + | }} | ||
| + | |||
| + | Таким образом задача сводится к поиску этой перестановки. Докажем, что полученный приведенным выше алгоритмом список является оптимальной перестановкой работ. | ||
| − | + | {{лемма | |
| − | {{ | ||
|id=lemma1 | |id=lemma1 | ||
|about=1 | |about=1 | ||
| − | |statement= Если для каких работ <tex> i </tex> и <tex> j </tex> из | + | |statement= Если для каких-то работ <tex> i </tex> и <tex> j </tex> из списка <tex> T </tex> верно неравенство <tex> \min(p_{i1}, p_{j2}) < \min(p_{j1}, p_{i2}) </tex>, то работа <tex> i </tex> встречается в списке <tex> T </tex> раньше, чем <tex> j </tex>. |
|proof= | |proof= | ||
Пусть <tex> p_{i1} < p_{j2} </tex>. Случай <tex> p_{i1} > p_{j2} </tex> рассматривается аналогично. | Пусть <tex> p_{i1} < p_{j2} </tex>. Случай <tex> p_{i1} > p_{j2} </tex> рассматривается аналогично. | ||
| − | + | Так как <tex> p_{i1} < \min(p_{j1}, p_{i2}) \leqslant p_{i2} </tex>, то работа <tex> i \in L </tex>. Работа <tex> j </tex> либо стоит в <tex> R </tex>, либо она стоит в <tex> L </tex> и при этом <tex> p_{i1} < p_{j1} </tex>. Заметим, что в обоих случаях она расположена позже (в силу нашего построения), чем работа <tex> i </tex>. | |
}} | }} | ||
| − | {{ | + | {{лемма |
|id=lemma2 | |id=lemma2 | ||
|about=2 | |about=2 | ||
| − | |statement= Пусть | + | |statement= Пусть имеем произвольное расписание, в котором работа <tex> j </tex> идет сразу же после работы <tex> i </tex>. Тогда если <tex> \min(p_{j1}, p_{i2}) \leqslant \min(p_{i1}, p_{j2}) </tex>, то можем поменять местами эти работы без ухудшения целевой функции. |
|proof= | |proof= | ||
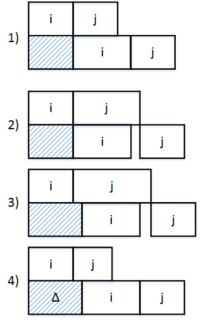
| − | + | [[Файл:f2cmax_fixed.png|200px|thumb|right|Рис. 2 {{---}} Расположение последовательных работ]] | |
| + | Пусть <tex> w_{ij} </tex> {{---}} время, прошедшее с начала выполнения работы <tex> i </tex> на первом станке до окончания работы <tex> j </tex> на втором станке. | ||
| + | |||
| + | Рассмотрим возможные случаи расположения работ <tex> i </tex> и <tex> j </tex> (см. Рис. 2) | ||
| + | <ol> | ||
| + | <li>Работа <tex> i </tex> начинается на втором станке сразу же после завершения ее на первом | ||
| + | <ul> | ||
| + | * Выполнение работы <tex> i </tex> на втором станке заканчивается позже, чем работы <tex> j </tex> на первом. | ||
| + | *: Тогда <tex> w_{ij} = p_{i1} + p_{i2} + p_{j2} </tex>. | ||
| + | * Выполнение работы <tex> i </tex> на втором станке заканчивается раньше, чем работы <tex> j </tex> на первом. | ||
| + | *: В этом случае <tex> w_{ij} = p_{i1} + p_{j1} + p_{j2} </tex>. | ||
| + | </ul> | ||
| + | </li> | ||
| + | <li>Работа <tex> i </tex> не может начаться на втором станке сразу же после завершения ее на первом | ||
| + | |||
| + | * Выполнение работы <tex> i </tex> на втором станке заканчивается раньше, чем работы <tex> j </tex> на первом. | ||
| + | *: Здесь снова имеем <tex> w_{ij} = p_{i1} + p_{j1} + p_{j2} </tex>. | ||
| + | * Выполнение работы <tex> i </tex> на втором станке заканчивается позже, чем работы <tex> j </tex> на первом. | ||
| + | *: Пусть <tex> \Delta </tex> {{---}} время прошедшее с начала выполнения работы <tex> i</tex> на первом станке и до начала ее выполнения на втором станке. Получили, что <tex> w_{ij} = \Delta + p_{i2} + p_{j2} </tex>. | ||
| + | |||
| + | </li> | ||
| + | </ol> | ||
| + | |||
| + | Таким образом, <tex> w_{ij} = \max (p_{i1} + p_{j1} + p_{j2}, p_{i1} + p_{i2} + p_{j2}, \Delta + p_{i2} + p_{j2}) </tex>. | ||
| + | |||
| + | Иначе говоря, <tex> w_{ij} = \max (p_{i1} + \max(p_{j1}, p_{i2}) + p_{j2}, \Delta + p_{i2} + p_{j2}) </tex>. | ||
| + | |||
| + | Аналогично, <tex> w_{ji} = \max (p_{j1} + \max(p_{i1}, p_{j2}) + p_{i2}, \Delta + p_{i2} + p_{j2}) </tex> | ||
| + | |||
| + | Так как <tex> \min(a, b) = - \max(-a, -b)</tex>, то из условия леммы имеем <tex> \max(-p_{i1}, -p_{j2}) \leqslant \max(-p_{j1}, -p_{i2}) </tex>. Добавив <tex> p_{i1} + p_{i2} + p_{j1} + p_{j2} </tex> к обеим частям, получим, что <tex> p_{j1} + \max(p_{i1}, p_{j2}) + p_{i2} \leqslant p_{i1} + \max(p_{j1}, p_{i2}) + p_{j2} </tex>, то есть <tex> w_{ji} \leqslant w_{ij} </tex> и при смене местами работ <tex> i </tex> и <tex> j </tex> ответ не ухудшается. | ||
| + | |||
| + | }} | ||
| + | |||
| + | |||
| + | {{ | ||
| + | Теорема|statement= | ||
| + | Построенная перестановка <tex> T </tex> является оптимальной. | ||
| + | |||
| + | |proof= | ||
| + | Рассмотрим произвольную перестановку <tex> S </tex>. Пусть перестановки <tex> T </tex> и <tex> S </tex> имеют общий префикс длины <tex> l-1 </tex>. Пусть <tex> i = T_{l} </tex> и <tex> j = S_{l} </tex>. Рассмотрим множество работ <tex>M = \{T_{r} \mid r = l, \dots, n\}</tex>. Заметим, что для любой работы <tex> k \in M </tex> верно, что <tex> \min(p_{k1}, p_{i2}) \geqslant \min(p_{i1}, p_{k2}) </tex>, так как если было бы верно обратное, то есть <tex> \min(p_{k1}, p_{i2}) < \min(p_{i1}, p_{k2}) </tex>, то по лемме 1 было бы верно, что <tex> k </tex> идет раньше <tex> i </tex>, что неверно. | ||
| + | |||
| + | Очевидно, что в перестановке <tex> S </tex> работа <tex> i </tex> будет стоять после <tex> j </tex> (иначе общий префикс был бы длиннее), то заметим, что в этой перестановке для работы <tex> i </tex> и для предыдущей работы <tex> w </tex> верно <tex> \min(p_{w1}, p_{i2}) \geqslant \min(p_{i1}, p_{w2}) </tex> (так как <tex> w \in M </tex>), то по лемме 2 можем поменять местами работы <tex> i </tex> и <tex> w </tex> без ухудшения ответа. То такими операциями сможем дойти до пары работ <tex> i </tex> и <tex> j </tex>, которые при смене увеличат общий префикс перестановок <tex> S </tex> и <tex> T </tex>. | ||
| + | |||
| + | Таким образом любая перестановка сводится к нашей без ухудшения ответа такими операциями, что подтверждает оптимальность перестановки <tex> T </tex> | ||
}} | }} | ||
==Псевдокод== | ==Псевдокод== | ||
| − | <tex> | + | |
| − | + | '''function''' F2Cmax(p: '''int'''[n][2]): '''list<int>''' | |
| − | + | '''list<int>''' L = <tex>\varnothing </tex> | |
| − | + | '''list<int>''' R = <tex>\varnothing </tex> | |
| − | + | '''set<int>''' X = <tex>\{1, \ldots, n\}</tex> | |
| − | + | '''while''' X <tex>\neq \varnothing</tex> | |
| − | + | Найти i и j, такие что <tex>p_{ij} = \min \{ p_{ij} \mid i \in X \land j = 1, 2\}</tex> | |
| − | + | '''if''' j == 1 | |
| − | + | L.addLast(i) | |
| − | + | '''else''' | |
| − | + | R.addFirst(i) | |
| − | + | X.remove(i) | |
| − | + | '''list<int>''' T = L ++ R | |
| − | + | '''return''' T | |
| − | |||
| − | |||
==Сложность алгоритма== | ==Сложность алгоритма== | ||
| − | Заметим, что на каждом шаге алгоритма мы выбираем минимум из оставшихся элементов за <tex>O(\log n)</tex> (либо предварительной сортировкой, либо любой | + | Заметим, что на каждом шаге алгоритма мы выбираем минимум из оставшихся элементов за <tex>O(\log n)</tex> (либо предварительной [[Сортировка|сортировкой]], либо с помощью любой структуры данных, поддерживающей нахождение минимума и удаление за <tex>O(\log n)</tex>, например, [[Двоичная_куча|кучи]]). А так как мы делаем это <tex> n </tex> раз, алгоритм работает за <tex>O(n\log n)</tex>. |
| + | |||
| + | ==См. также== | ||
| + | * [[J2ni2Cmax|<tex>J2 \mid n_i \leqslant 2 \mid C_{max}</tex>]] | ||
| + | * [[O2Cmax|<tex>O2\mid\mid C_{max}</tex>]] | ||
| + | * [[R2Cmax|<tex>R2\mid\mid C_{max}</tex>]] | ||
| − | ==Источники== | + | ==Источники информации== |
* Peter Brucker. «Scheduling Algorithms» {{---}} «Springer», 2006 г. {{---}} 175 стр. {{---}} ISBN 978-3-540-69515-8 | * Peter Brucker. «Scheduling Algorithms» {{---}} «Springer», 2006 г. {{---}} 175 стр. {{---}} ISBN 978-3-540-69515-8 | ||
| − | [[Категория: | + | [[Категория: Алгоритмы и структуры данных]] |
[[Категория: Теория расписаний]] | [[Категория: Теория расписаний]] | ||
Текущая версия на 19:27, 4 сентября 2022
| Задача: |
Рассмотрим задачу:
|
Содержание
Описание алгоритма
Пусть — время выполнения -ой работы на первом станке, а — на втором.
- Алгоритм строит два списка и . Изначально они пусты. Также поддерживается множество еще не распределенных по спискам и работ
- Пока множество не пусто, распределяем работы по спискам следующим образом:
- находим такие индексы и , что ,
- если минимум достигается на первом станке (иными словами ), то поставим работу в конец списка , иначе ставим в начало списка ,
- удаляем работу из множества .
- Рассмотрим список — конкатенацию и . Утверждается, что этот список является оптимальной перестановкой работ как на первом, так и на втором станке. Далее расставляем подряд работы на первом станке согласно перестановке, после чего ставим в том же порядке работы на втором станке, при этом избегая одновременного выполнения одной и той же работы.
Доказательство корректности алгоритма
| Теорема: |
Существует оптимальное расписание, в котором станки выполняют работы в одном и том же порядке. |
| Доказательство: |
|
Предположим обратное: что не существует оптимального расписания с одинаковыми перестановками работ на станках. Рассмотрим некоторое оптимальное расписание с максимальным по длине общим префиксом на станках. Пусть его длина равна , где . Пусть на позиции на первом и втором станках стоит работа , а на втором станке на позиции стоит работа . Тогда заметим, что если мы поставим работу на первом станке сразу после работы , то последовательные работы с по (см. рис. 1) по-прежнему будут успевать выполниться, так как на втором станке они выполняются в текущем расписании после . Таким образом нам удалось увеличить длину наибольшего общего префикса, а так как по нашему предположению она была максимальна, то предположение неверно и искомое расписание с одинаковым порядком выполнения работ на обоих станках существует. |
Таким образом задача сводится к поиску этой перестановки. Докажем, что полученный приведенным выше алгоритмом список является оптимальной перестановкой работ.
| Лемма (1): |
Если для каких-то работ и из списка верно неравенство , то работа встречается в списке раньше, чем . |
| Доказательство: |
|
Пусть . Случай рассматривается аналогично. Так как , то работа . Работа либо стоит в , либо она стоит в и при этом . Заметим, что в обоих случаях она расположена позже (в силу нашего построения), чем работа . |
| Лемма (2): |
Пусть имеем произвольное расписание, в котором работа идет сразу же после работы . Тогда если , то можем поменять местами эти работы без ухудшения целевой функции. |
| Доказательство: |
|
Пусть — время, прошедшее с начала выполнения работы на первом станке до окончания работы на втором станке. Рассмотрим возможные случаи расположения работ и (см. Рис. 2)
Таким образом, . Иначе говоря, . Аналогично, Так как , то из условия леммы имеем . Добавив к обеим частям, получим, что , то есть и при смене местами работ и ответ не ухудшается. |
| Теорема: |
Построенная перестановка является оптимальной. |
| Доказательство: |
|
Рассмотрим произвольную перестановку . Пусть перестановки и имеют общий префикс длины . Пусть и . Рассмотрим множество работ . Заметим, что для любой работы верно, что , так как если было бы верно обратное, то есть , то по лемме 1 было бы верно, что идет раньше , что неверно. Очевидно, что в перестановке работа будет стоять после (иначе общий префикс был бы длиннее), то заметим, что в этой перестановке для работы и для предыдущей работы верно (так как ), то по лемме 2 можем поменять местами работы и без ухудшения ответа. То такими операциями сможем дойти до пары работ и , которые при смене увеличат общий префикс перестановок и . Таким образом любая перестановка сводится к нашей без ухудшения ответа такими операциями, что подтверждает оптимальность перестановки |
Псевдокод
function F2Cmax(p: int[n][2]): list<int>
list<int> L =
list<int> R =
set<int> X =
while X
Найти i и j, такие что
if j == 1
L.addLast(i)
else
R.addFirst(i)
X.remove(i)
list<int> T = L ++ R
return T
Сложность алгоритма
Заметим, что на каждом шаге алгоритма мы выбираем минимум из оставшихся элементов за (либо предварительной сортировкой, либо с помощью любой структуры данных, поддерживающей нахождение минимума и удаление за , например, кучи). А так как мы делаем это раз, алгоритм работает за .
См. также
Источники информации
- Peter Brucker. «Scheduling Algorithms» — «Springer», 2006 г. — 175 стр. — ISBN 978-3-540-69515-8