Многопоточная сортировка слиянием — различия между версиями
м (rollbackEdits.php mass rollback) |
|
| (не показана 1 промежуточная версия 1 участника) | |
(нет различий)
| |
Текущая версия на 19:27, 4 сентября 2022
Содержание
Многопоточная сортировка слиянием
Благодаря тому, что сортировка слиянием построена на принципе "Разделяй и властвуй", выполнение данного алгоритма можно весьма эффективно распараллелить. При оценке асимптотики допускается, что возможен запуск неограниченного количества независимых процессов, т.е. процессов с вычислительными ресурсами, не зависящими от других процессов, что на практике не достижимо. Более того, при реализации имеет смысл ограничить количество параллельных потоков.
Сортировка с однопоточным слиянием
Внесем в алгоритм сортировки слиянием следующую модификацию: будем сортировать левую и правую части массива параллельно.
function mergeSortMT(array, left, right):
mid = (left + right) / 2
spawn mergeSortMT(array, left, mid)
mergeSortMT(array, mid + 1, right)
sync
merge(array, left, mid, right)
В данном алгоритме оператор запускает новый поток, а оператор ожидает завершения этого потока. Функция аналогична одноименной функции из раздела слияние двух массивов.
Несмотря на наличие двух рекурсивных вызовов, при оценке будем считать, что совершается один вызов, т.к. оба вызова выполняются параллельно с одинаковой асимптотикой. Оценим время работы данного алгоритма: . Данная асимптотика достигается при возможности запускать неограниченное количество потоков независимо друг от друга.
Многопоточное слияние
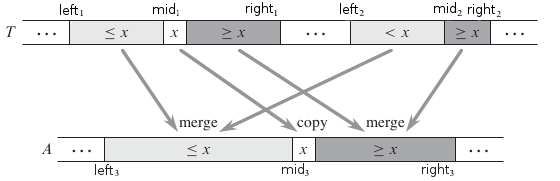
Как видно из оценки первого алгоритма, слияние является его узким местом. Попытаемся распараллелить слияние, для чего рассмотрим алгоритм рекурсивного слияния массивов и в массив :
- Убедимся, что размер больше либо равен размеру
- Возьмем — середину первого массива ( также является и медианой этого массива)
- При помощи бинарного поиска найдем такое, что
- Сольем и в
- Сольем и в
Алгоритм показан на рисунке:
Реализация
// если возвращает // если , возвращает // иначе возвращает наибольший индекс из отрезка такой, что integer binarySearch(x, array, left, right) // слияние и в function mergeMT(T, left, right, left, right, A, left): n = right - left + 1 n = right - left + 1 if n < n swap(left, left) swap(right, right) swap(n, n) if n == 0 return else mid = (left + right) / 2 mid = binarySearch(T[mid], T, left, right) mid = left + (mid - left) + (mid - left) A[mid] = T[mid] spawn mergeMT(T, left, mid - 1, left, mid - 1, A, left) mergeMT(T, mid + 1, right, mid, right, A, mid + 1) sync
Оба массива содержат элементов. К моменту рекурсивных вызовов , значит,
.
В худшем случае один из двух рекурсивных вызовов сольет элементов с элементами и тогда количество элементов первых двух массивов в рекурсивном вызове будет равно
.
Асимптотика каждого вызова функции — , т.е. время, затрачиваемое на бинарный поиск. Так как рекурсивные вызовы функции выполняются параллельно, а потоки при оценке независимы, время их выполнения будет равно времени выполнения самого долгого вызова. В худшем случае это . Тогда получим оценку сверху
Сортировка с многопоточным слиянием
Приведем псевдокод алгоритма, использующего слияние из предыдущего раздела, сортирующего элементы и помещающего отсортированный массив в
function mergeSortMT2(A, leftA, rightA, B, leftB):
n = r - p + 1
if n == 1
B[leftB] = A[leftA]
else
создадим новый массив T[1 n]
mid = (leftA + rightA) / 2
newMid = mid - leftA + 1
spawn mergeSortMT2(A, leftA, mid, T, 1)
mergeSortMT2(A, mid + 1, rightA, T, newMid + 1)
sync
mergeMT(T, 1, newMid, newMid + 1, n, B, leftB)
Оценим данный алгоритм сверху при условии, что возможен запуск неограниченного количества независимых потоков. Из предыдущих пунктов .
Оценка при фиксированном числе потоков
Понятно, что при отсутствии возможности запуска неограниченного количества независимых потоков, вычислительная сложность многопоточного алгоритма зависит от максимально возможного количества независимых потоков. Обозначим такое количество как . Допустим, много больше , что в общем случае верно для ПК и достаточно больших объемов данных. Оценим приведенные выше алгоритмы с учетом наложенных ограничений и допущений:
- Сортировка с однопоточным слиянием будет иметь асимптотику :
- операций нужно на последовательную сортировку массива длиной .
- необходимо на последовательное слияние.
- Многопоточное слияние будет работать за :
- Прежде чем достигнуть ограничения на создание нового потока, алгоритм углубится на уровней вглубь дерева рекурсии, где на каждом уровне выполняется бинпоиск за
- Асимптотика многопоточного слияния при работе в одном потоке по основной теореме рекуррентных соотношений равна
- Оценим сортировку с многопоточным слиянием снизу:
- Части массива длиной гарантированно будут сортироваться последовательно, т.к. только алгоритм сортировки запустит к моменту вызова от массива длиной число потоков, равное . Тогда по основной теореме рекуррентных соотношений:
- Сортировка с однопоточным слиянием будет иметь асимптотику :
Очевидно, что нижняя оценка алгоритма сортировки с многопоточным слиянием выше. Таким образом, при приведенных выше допущениях алгоритм сортировки с однопоточным слиянием эффективнее и его асимптотика составляет .
См. также
Источники информации
- Cormen T.H., Leiserson C.E., Rivest R.L., Stein C. — Introduction to Algorithms, Third Edition