Heavy-light декомпозиция — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 68 промежуточных версий 6 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Heavy-light декомпозиция''' {{---}} техника разбиения дерева на множество | + | '''Heavy-light декомпозиция''' {{---}} техника разбиения подвешенного дерева на множество путей для решения задач о запросах на пути в дереве (в том числе с модификациями). |
==Описание задачи== | ==Описание задачи== | ||
| − | + | {{Задача | |
| + | |definition=Имеется подвешенное дерево <tex>T</tex> c <tex>n</tex> вершинами и необходимо проводить операции на нем на пути от вершины <tex>v</tex> до вершины <tex>u</tex>.}} | ||
| + | Примеры запросов: | ||
| + | <ul> | ||
| + | <li>сумма на пути,</li> | ||
| + | <li>максимум на пути,</li> | ||
| + | <li>количество рёбер на пути, вес которых больше заданного <tex>c</tex>.</li> | ||
| + | </ul> | ||
| + | |||
| + | Примеры модификаций: | ||
| + | <ul> | ||
| + | <li>модификация одного ребра,</li> | ||
| + | <li>прибавление к весу всех рёбер на пути,</li> | ||
| + | <li>установка веса всех рёбер на пути в заданное <tex>c</tex>.</li> | ||
| + | </ul> | ||
| + | |||
| + | Множество подобных запросов делаются за время за полином от логарифма (обычно <tex>O(\log^2{n})</tex>) с помощью heavy-light декомпозиции. | ||
==Описание декомпозиции== | ==Описание декомпозиции== | ||
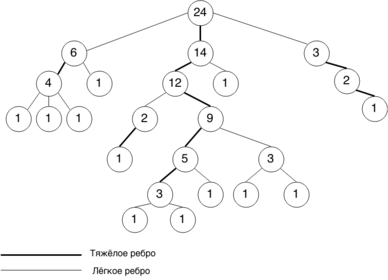
| − | [[Файл:Heavylight.png|thumb|right| | + | [[Файл:Heavylight.png|thumb|right|800x280px|Пример разбиения. В вершинах указан размер поддерева.]] |
| − | Декомпозиция заключается в классификации всех рёбер дерева <tex>T</tex> в 2 вида: легкие и тяжёлые. Введём функцию <tex>s(v)</tex>, которая будет обозначать размер поддерева вершины <tex>v</tex>. | + | Необходимо составить такую декомпозицию дерева на множество рёберно-непересекающихся путей, что при прохождении от одной вершины до другой произойдет смена не более <tex>O(\log{n})</tex> путей из декомпозиции. |
| + | |||
| + | Декомпозиция заключается в классификации всех рёбер дерева <tex>T</tex> в <tex>2</tex> вида: легкие и тяжёлые. Введём функцию <tex>s(v)</tex>, которая будет обозначать размер поддерева вершины <tex>v</tex>. | ||
| + | |||
| + | '''Тяжёлые ребра''' (англ. ''heavy edge'') {{---}} ребра <tex>(u, v)</tex> такие, что <tex>s(v) \geqslant</tex> <tex dpi="150">\dfrac{s(u)}{2}</tex>. | ||
| − | ''' | + | '''Лёгкие ребра''' (англ. ''light edge'') {{---}} соответственно все остальные. |
| − | + | Очевидно, что из вершины может выходить как максимум одно тяжёлое ребро, т.к. иначе у нас есть два поддерева по как минимум <tex dpi="150">\dfrac{s(u)}{2}</tex> вершин, а также сама вершина <tex>u</tex>. Итого <tex>s(u) + 1</tex> вершин, тогда как у нас всего <tex>s(u)</tex> вершин в поддереве. | |
| − | + | Теперь рассмотрим вершины, из которых не ведет вниз ни одно тяжёлое ребро. Будем идти от них вверх до корня или пока не пройдем легкое ребро. Получится какое-то множество путей. Утверждается, что полученная таким образом декомпозиция будет являться искомой и корректной. | |
| − | |||
| − | |||
{{Утверждение | {{Утверждение | ||
|statement = Полученная декомпозиция является искомой. | |statement = Полученная декомпозиция является искомой. | ||
|proof = | |proof = | ||
Докажем по отдельности корректность декомпозиции. | Докажем по отдельности корректность декомпозиции. | ||
| + | # Все рёбра покрыты путями. <br>Есть два типа вершин: те, из которых ведёт ровно одно тяжёлое ребро и те, из которых не ведёт ни одного тяжёлого ребра. Для первого типа вершин мы дойдем до них некоторым путём через тяжёлое ребро снизу по определению выбора путей, а лёгкие рёбра ведущие из неё возьмем как последние рёбра в соответствующих путях. Для второго типа вершин мы по определению выбора путей возьмем их как начальные и пойдем вверх. <br>Таким образом все рёбра будут покрыты. | ||
| + | # Все пути не пересекаются. <br>Докажем от противного. Пусть мы взяли какое-то ребро дважды. Это значит, что из какой-то вершины <tex>v</tex> ведет более <tex>1</tex> тяжелого ребра в детей. Эти ребра относятся к разным путями, однако пути имеют хотя бы общее ребро {{---}} ребро из <tex>v</tex> в отца <tex>v</tex>. Более <tex>1</tex> тяжелого ребра из вершины идти не может, следовательно, получили противоречие. | ||
| + | # При прохождении пути от вершины <tex>v</tex> до вершины <tex>u</tex> произойдет смена не более, чем <tex>O(\log{n})</tex> путей. <br>Докажем эквивалентный факт, что при пути от любой вершины до корня мы сменим не более, чем <tex>O(\log{n})</tex> путей. Рассмотрим лёгкое ребро. Заметим, что проход вниз по такому ребру уменьшает размер поддерева как минимум в <tex>2</tex> раза. Но смена пути может произойти только при переходе по лёгкому ребру. Таким образом мы сменим не более <tex>O(\log{n})</tex> путей. | ||
| + | }} | ||
| + | |||
| − | + | Существует вариант heavy-light декомпозиции на вершинно-непересекающихся путях. Чтобы получить такой путь нужно всего-лишь выкинуть последнее ребро из всех путей в рёберно-непересекающейся декомпозиции. Это может быть удобно при решении задач, где веса находятся не на рёбрах, а на вершинах и соответствующие запросы также делаются на вершинах. | |
| − | + | ==Применение== | |
| + | ===Сумма на пути=== | ||
| + | Классическая задача о сумме на пути в дереве с <tex>n</tex> вершинами может быть решена с помощью heavy-light декомпозиции за время <tex>O(\log^2{n})</tex>. Возможны модификации веса. | ||
| − | + | Построим [[Дерево отрезков. Построение|дерево отрезков]] над каждым путём. Рассмотрим запрос <tex>sum(u, v)</tex>. Найдем вершину <tex>c</tex>, которая является <tex>\mathrm{LCA}(u, v)</tex> (например с помощью [[Метод двоичного подъема|двоичного подъема]]. Мы разбили запрос на два: <tex>(u, c)</tex> и <tex>(c, v)</tex>, на каждый из которых можно легко ответить разбив его на множество путей из декомпозиции и ответив на каждый путь из этого множества по отдельности за <tex>O(\log{n})</tex> с помощью дерева отрезков на этом пути. Всего таких путей нужно будет рассмотреть <tex>O(\log{n})</tex>. Итого мы способны решить эту задачу за время <tex>O(\log^2{n})</tex>. | |
| − | + | Хоть это и не самый эффективный способ для решения этой задачи, но можно заметить, что навесив дерево отрезков на каждый путь мы способны отвечать на любые операции, определяемые на множестве, на котором данная операция ассоциативна, и существует нейтральный элемент относительно этой операции, то есть на моноиде (операции, поддерживаемые деревом отрезков), такие как: сумма на пути, максимум на пути, количество рёбер на пути, удовлетворяющих какому-то свойству. | |
| + | ===LCA=== | ||
| + | Задача о наименьшем общем предке для двух вершин в дереве с <tex>n</tex> вершинами также может быть решена с помощью heavy-light декомпозиции. Воспользуемся основной идеей: декомпозиция разбивает все вершины дерева на реберно-непересекающиеся пути так, что поднимаясь от любой вершины до корня дерева придется сменить не более <tex>\log{n}</tex> различных путей. | ||
| − | + | {{Лемма | |
| + | |id=Лемма1 | ||
| + | |statement=Пусть есть вершины <tex>u</tex> и <tex>v</tex>, лежащие на разных путях. При этом <tex>U</tex>, <tex>V</tex> — корни путей, на которых они лежат. Если <tex>U</tex> более удален от корня дерева, чем <tex>V</tex>, то <tex>\mathrm{LCA}(u, v) = \mathrm{LCA}(U, v)</tex>. | ||
| − | + | |proof=Допустим, пути не пересекаются. Предположим, что <tex>\mathrm{LCA}(u, v)</tex> и <tex>\mathrm{LCA}(U, v)</tex> это разные вершины. Тогда существует вершина, на пути от <tex>u</tex> к <tex>U</tex>, являющаяся <tex>\mathrm{LCA}</tex>. Значит <tex>\mathrm{LCA}</tex> должен принадлежать двум путям, но по предположению пути не пересекаются. Тем самым пришли к противоречию. | |
| − | + | Теперь рассмотрим случай, когда пути пересекаются. Пути не могут совпадать более, чем в одной вершине, так как построенная декомпозиция является реберно-непересекающейся. При этом корень одного из путей является вершиной другого (либо корни совпадают, что равносильно), поскольку в противном случае пути пересекаются в более чем <tex>1</tex> вершине, что противоречит предыдущему условию. <tex>\mathrm{LCA}</tex> должен принадлежать двум путям, значит именно этот корень и будет <tex>\mathrm{LCA}</tex>. | |
}} | }} | ||
| − | == | + | ====Препроцессинг==== |
| − | === | + | Построим heavy-light декомпозицию данного нам дерева. Для каждой вершины, помимо её предка, будем хранить дополнительно следующие значения: |
| − | + | # Расстояние до корня дерева. <br />Вычисляется за <tex>O(1)</tex> с помощью времен входа\выхода в каждую вершину. | |
| + | # Корень пути, на котором лежит вершина. <br /> Поскольку вершина может принадлежать нескольким путям, выберем тот, чья начальная вершина наиболее удалена от корня дерева. Имея разбиение на пути, найти корень можно за <tex>O(1)</tex>. | ||
| + | # Вторая вершина этого пути. <br />Аналогично, находится за <tex>O(1)</tex> при построении. | ||
| + | |||
| + | ====Вычисление LCA==== | ||
| + | Найдем <tex>\mathrm{LCA}</tex> для двух вершин. Для этого будем рекурсивно подниматься от этих вершин в направлении корня. Пусть на данной итерации рассматриваем вершины <tex>u</tex> и <tex>v</tex>. Заметим, что если эти вершины лежат на одном пути, то ответ {{---}} это такая вершина (<tex>u</tex> или <tex>v</tex>), которая находится ближе к корню. Очевидно, что если расстояние от корня до <tex>u</tex> меньше, чем расстояние до <tex>v</tex>, то <tex>u</tex> является предком <tex>v</tex>. Иначе, наоборот. | ||
| + | |||
| + | Для проверки этого условия недостаточно знать только корни путей, потому что несколько путей могу иметь общий корень. Но любые два пути пересекаются не более чем в одной вершине. Воспользуемся этим фактом. | ||
| + | |||
| + | Пусть <tex>a</tex> и <tex>b</tex> {{---}} вторые вершины путей, содержащих вершины <tex>u</tex> и <tex>v</tex> соответственно. Важно заметить, что любая вершина, помимо корня дерева является некорневой вершиной какого-либо другого пути, поэтому такие <tex>a</tex> и <tex>b</tex> всегда существуют. | ||
| + | |||
| + | * Заметим, что если <tex>a</tex> = <tex>b</tex>, то <tex>u</tex> и <tex>v</tex> лежат на одном пути. Этот случай мы уже рассмотрели ранее. | ||
| + | |||
| + | * Если это не так, то вершины лежат на разных путях. По лемме, так как пути реберно не пересекаются, то ответ не изменится, если вместо одной из вершин взять корень того пути, на котором она лежит. Эту операцию будем производить с той вершиной, чей предок наиболее удален от корня. Рекурсивно запустимся от выбранной и оставшейся вершин. | ||
| + | |||
| + | Очевидно, что в результате придем или в одну и ту же вершину, или одна из вершин окажется на пути от корня к другой. Тем самым мы найдем <tex>\mathrm{LCA}</tex>. | ||
| + | |||
| + | ====Псевдокод==== | ||
| + | |||
| + | Объявим несколько массивов для хранения дополнительной информации: | ||
| + | * <tex>\mathtt{dist}</tex> {{---}} расстояние от корня до вершины. | ||
| + | * <tex>\mathtt{last}</tex> {{---}} начало пути, на котором лежит вершина. Из всех путей выбирается путь с самой удаленной от корня дерева начальной вершины. | ||
| + | * <tex>\mathtt{turn}</tex> {{---}} вторая вершина этого пути. | ||
| − | + | Ниже представлен псевдокод функции получения наименьшего общего предка: | |
| + | |||
| + | <font color=darkgreen>// Находит наименьшего общего предка вершин <tex>u</tex> и <tex>v</tex></font> | ||
| + | '''int''' lca('''int''' u, '''int''' v) | ||
| + | <font color=darkgreen>// Проверяем вторые вершины путей, содержащих <tex>u</tex> и <tex>v</tex>.</font> | ||
| + | '''if''' (turn[u] == turn[v]) | ||
| + | <font color=darkgreen>// Ответ найден, выберем ближайшую к корню.</font> | ||
| + | '''if''' (dist[u] < dist[v]) | ||
| + | '''return''' u | ||
| + | '''else''' | ||
| + | '''return''' v | ||
| + | |||
| + | <font color=darkgreen>// Рекурсивно запустимся от вершины, чей предок наиболее удален от корня дерева.</font> | ||
| + | '''if''' (dist[last[u]] > dist[last[v]]) | ||
| + | '''return''' lca(last[u], v) | ||
| + | '''return''' lca(last[v], u) | ||
| − | + | ====Асимптотика==== | |
| + | * '''Память''': для реализации алгоритма требуется <tex>O(n)</tex> памяти. | ||
| + | * '''Препроцессинг''': heavy-light декомпозиция строится за <tex>O(n)</tex>, вся дополнительная информация считается за <tex>O(1)</tex> для каждой из вершин. | ||
| + | * '''Запросы''': по свойству heavy-light декомпозиции, на пути от вершины к корню мы сменим не более <tex>\log n</tex> путей. Значит время выполнения запроса также <tex>O(\log n)</tex>. | ||
| − | |||
==Реализация== | ==Реализация== | ||
| − | + | Ниже будет приведена реализация запроса сумма на пути между любыми двумя вершинами в дереве без запросов модификации. Все запросы, сводящиеся к навешиванию дерева отрезков на пути из декомпозиции делаются похожим образом. | |
| + | |||
| + | Опущены некоторые детали реализации: построение и дерево отрезков. | ||
| + | <ul> | ||
| + | <li><tex>\mathrm{pathPos}</tex> {{---}} функция, позволяющая найти смещение вершины в пути относительно корня пути,</li> | ||
| + | <li><tex>\mathrm{getValue(\mathtt{i}, \mathtt{j})}</tex> {{---}} функция, позволяющая найти вес <tex>\mathtt{j}</tex>-ого ребра в <tex>\mathtt{i}</tex>-ом пути.</li> | ||
| + | </ul> | ||
| + | Пример реализации запроса суммы на пути: | ||
| + | |||
| + | '''int''' query('''int''' u, '''int''' v) | ||
| + | '''int''' res = 0 | ||
| + | '''int''' root = корень пути, в котором находится u | ||
| + | '''while''' root не является предком v <font color=green> // поднимаемся до тех пор, пока наш путь не содержит общего предка u и v</font> | ||
| + | segmentTree = дерево отрезков, соответствующее пути, в котором лежит u | ||
| + | res += segmentTree.sum(0, pathPos(u)) | ||
| + | u = предок root <font color=green> // вырезали нижний путь и подняли нижнюю вершину до нижней вершины следующего пути</font> | ||
| + | root = корень пути, в котором находится u | ||
| + | |||
| + | root = корень пути, в котором находится v | ||
| + | '''while''' root не является предком u <font color=green> // аналогично прошлому while, но с другой стороны</font> | ||
| + | segmentTree = дерево отрезков, соответствующее пути, в котором лежит v | ||
| + | res += segmentTree.sum(0, pathPos(v)) | ||
| + | v = предок root | ||
| + | root = корень пути, в котором находится v | ||
| + | |||
| + | <font color=green>// последний путь (тот, что содержит общего предка) обрезан с двух сторон полученными вершинами</font> | ||
| + | segmentTree = дерево отрезков, соответствующее пути в котором лежит u | ||
| + | res += segmentTree.sum(min(pathPos(u), pathPos(v)), max(pathPos(u), pathPos(v))) | ||
| + | '''return''' res | ||
| + | |||
| + | == См.также == | ||
| + | *[[Метод двоичного подъема]] | ||
| + | *[[Дерево отрезков. Построение]] | ||
| + | *[[Link-Cut Tree]] | ||
| + | |||
| + | ==Источники информации== | ||
| + | *[http://en.wikipedia.org/wiki/Heavy_path_decomposition Wikipedia — Heavy path decomposition] | ||
| + | *[http://e-maxx.ru/algo/heavy_light MAXimal :: algo :: Heavy-light декомпозиция] | ||
| + | * [https://habrahabr.ru/post/198464 Habrahabr {{---}} Алгоритм поиска наименьшего общего предка в дереве ] | ||
| + | |||
| + | [[Категория: Алгоритмы и структуры данных]] | ||
| + | [[Категория: Задача о наименьшем общем предке]] | ||
| + | [[Категория: Структуры данных]] | ||
Текущая версия на 19:27, 4 сентября 2022
Heavy-light декомпозиция — техника разбиения подвешенного дерева на множество путей для решения задач о запросах на пути в дереве (в том числе с модификациями).
Содержание
Описание задачи
| Задача: |
| Имеется подвешенное дерево c вершинами и необходимо проводить операции на нем на пути от вершины до вершины . |
Примеры запросов:
- сумма на пути,
- максимум на пути,
- количество рёбер на пути, вес которых больше заданного .
Примеры модификаций:
- модификация одного ребра,
- прибавление к весу всех рёбер на пути,
- установка веса всех рёбер на пути в заданное .
Множество подобных запросов делаются за время за полином от логарифма (обычно ) с помощью heavy-light декомпозиции.
Описание декомпозиции
Необходимо составить такую декомпозицию дерева на множество рёберно-непересекающихся путей, что при прохождении от одной вершины до другой произойдет смена не более путей из декомпозиции.
Декомпозиция заключается в классификации всех рёбер дерева в вида: легкие и тяжёлые. Введём функцию , которая будет обозначать размер поддерева вершины .
Тяжёлые ребра (англ. heavy edge) — ребра такие, что .
Лёгкие ребра (англ. light edge) — соответственно все остальные.
Очевидно, что из вершины может выходить как максимум одно тяжёлое ребро, т.к. иначе у нас есть два поддерева по как минимум вершин, а также сама вершина . Итого вершин, тогда как у нас всего вершин в поддереве.
Теперь рассмотрим вершины, из которых не ведет вниз ни одно тяжёлое ребро. Будем идти от них вверх до корня или пока не пройдем легкое ребро. Получится какое-то множество путей. Утверждается, что полученная таким образом декомпозиция будет являться искомой и корректной.
| Утверждение: |
Полученная декомпозиция является искомой. |
|
Докажем по отдельности корректность декомпозиции.
|
Существует вариант heavy-light декомпозиции на вершинно-непересекающихся путях. Чтобы получить такой путь нужно всего-лишь выкинуть последнее ребро из всех путей в рёберно-непересекающейся декомпозиции. Это может быть удобно при решении задач, где веса находятся не на рёбрах, а на вершинах и соответствующие запросы также делаются на вершинах.
Применение
Сумма на пути
Классическая задача о сумме на пути в дереве с вершинами может быть решена с помощью heavy-light декомпозиции за время . Возможны модификации веса.
Построим дерево отрезков над каждым путём. Рассмотрим запрос . Найдем вершину , которая является (например с помощью двоичного подъема. Мы разбили запрос на два: и , на каждый из которых можно легко ответить разбив его на множество путей из декомпозиции и ответив на каждый путь из этого множества по отдельности за с помощью дерева отрезков на этом пути. Всего таких путей нужно будет рассмотреть . Итого мы способны решить эту задачу за время .
Хоть это и не самый эффективный способ для решения этой задачи, но можно заметить, что навесив дерево отрезков на каждый путь мы способны отвечать на любые операции, определяемые на множестве, на котором данная операция ассоциативна, и существует нейтральный элемент относительно этой операции, то есть на моноиде (операции, поддерживаемые деревом отрезков), такие как: сумма на пути, максимум на пути, количество рёбер на пути, удовлетворяющих какому-то свойству.
LCA
Задача о наименьшем общем предке для двух вершин в дереве с вершинами также может быть решена с помощью heavy-light декомпозиции. Воспользуемся основной идеей: декомпозиция разбивает все вершины дерева на реберно-непересекающиеся пути так, что поднимаясь от любой вершины до корня дерева придется сменить не более различных путей.
| Лемма: |
Пусть есть вершины и , лежащие на разных путях. При этом , — корни путей, на которых они лежат. Если более удален от корня дерева, чем , то . |
| Доказательство: |
|
Допустим, пути не пересекаются. Предположим, что и это разные вершины. Тогда существует вершина, на пути от к , являющаяся . Значит должен принадлежать двум путям, но по предположению пути не пересекаются. Тем самым пришли к противоречию. Теперь рассмотрим случай, когда пути пересекаются. Пути не могут совпадать более, чем в одной вершине, так как построенная декомпозиция является реберно-непересекающейся. При этом корень одного из путей является вершиной другого (либо корни совпадают, что равносильно), поскольку в противном случае пути пересекаются в более чем вершине, что противоречит предыдущему условию. должен принадлежать двум путям, значит именно этот корень и будет . |
Препроцессинг
Построим heavy-light декомпозицию данного нам дерева. Для каждой вершины, помимо её предка, будем хранить дополнительно следующие значения:
- Расстояние до корня дерева.
Вычисляется за с помощью времен входа\выхода в каждую вершину. - Корень пути, на котором лежит вершина.
Поскольку вершина может принадлежать нескольким путям, выберем тот, чья начальная вершина наиболее удалена от корня дерева. Имея разбиение на пути, найти корень можно за . - Вторая вершина этого пути.
Аналогично, находится за при построении.
Вычисление LCA
Найдем для двух вершин. Для этого будем рекурсивно подниматься от этих вершин в направлении корня. Пусть на данной итерации рассматриваем вершины и . Заметим, что если эти вершины лежат на одном пути, то ответ — это такая вершина ( или ), которая находится ближе к корню. Очевидно, что если расстояние от корня до меньше, чем расстояние до , то является предком . Иначе, наоборот.
Для проверки этого условия недостаточно знать только корни путей, потому что несколько путей могу иметь общий корень. Но любые два пути пересекаются не более чем в одной вершине. Воспользуемся этим фактом.
Пусть и — вторые вершины путей, содержащих вершины и соответственно. Важно заметить, что любая вершина, помимо корня дерева является некорневой вершиной какого-либо другого пути, поэтому такие и всегда существуют.
- Заметим, что если = , то и лежат на одном пути. Этот случай мы уже рассмотрели ранее.
- Если это не так, то вершины лежат на разных путях. По лемме, так как пути реберно не пересекаются, то ответ не изменится, если вместо одной из вершин взять корень того пути, на котором она лежит. Эту операцию будем производить с той вершиной, чей предок наиболее удален от корня. Рекурсивно запустимся от выбранной и оставшейся вершин.
Очевидно, что в результате придем или в одну и ту же вершину, или одна из вершин окажется на пути от корня к другой. Тем самым мы найдем .
Псевдокод
Объявим несколько массивов для хранения дополнительной информации:
- — расстояние от корня до вершины.
- — начало пути, на котором лежит вершина. Из всех путей выбирается путь с самой удаленной от корня дерева начальной вершины.
- — вторая вершина этого пути.
Ниже представлен псевдокод функции получения наименьшего общего предка:
// Находит наименьшего общего предка вершин и int lca(int u, int v) // Проверяем вторые вершины путей, содержащих и . if (turn[u] == turn[v]) // Ответ найден, выберем ближайшую к корню. if (dist[u] < dist[v]) return u else return v // Рекурсивно запустимся от вершины, чей предок наиболее удален от корня дерева. if (dist[last[u]] > dist[last[v]]) return lca(last[u], v) return lca(last[v], u)
Асимптотика
- Память: для реализации алгоритма требуется памяти.
- Препроцессинг: heavy-light декомпозиция строится за , вся дополнительная информация считается за для каждой из вершин.
- Запросы: по свойству heavy-light декомпозиции, на пути от вершины к корню мы сменим не более путей. Значит время выполнения запроса также .
Реализация
Ниже будет приведена реализация запроса сумма на пути между любыми двумя вершинами в дереве без запросов модификации. Все запросы, сводящиеся к навешиванию дерева отрезков на пути из декомпозиции делаются похожим образом.
Опущены некоторые детали реализации: построение и дерево отрезков.
- — функция, позволяющая найти смещение вершины в пути относительно корня пути,
- — функция, позволяющая найти вес -ого ребра в -ом пути.
Пример реализации запроса суммы на пути:
int query(int u, int v)
int res = 0
int root = корень пути, в котором находится u
while root не является предком v // поднимаемся до тех пор, пока наш путь не содержит общего предка u и v
segmentTree = дерево отрезков, соответствующее пути, в котором лежит u
res += segmentTree.sum(0, pathPos(u))
u = предок root // вырезали нижний путь и подняли нижнюю вершину до нижней вершины следующего пути
root = корень пути, в котором находится u
root = корень пути, в котором находится v
while root не является предком u // аналогично прошлому while, но с другой стороны
segmentTree = дерево отрезков, соответствующее пути, в котором лежит v
res += segmentTree.sum(0, pathPos(v))
v = предок root
root = корень пути, в котором находится v
// последний путь (тот, что содержит общего предка) обрезан с двух сторон полученными вершинами
segmentTree = дерево отрезков, соответствующее пути в котором лежит u
res += segmentTree.sum(min(pathPos(u), pathPos(v)), max(pathPos(u), pathPos(v)))
return res