Пересечение всех максимальных по включению барьеров — различия между версиями
Scuuter (обсуждение | вклад) м |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 4 промежуточные версии 2 участников) | |||
| Строка 16: | Строка 16: | ||
|statement = Пересечение всех максимальных по включению барьеров графа <tex>G</tex> равно <tex>A(G)</tex>. | |statement = Пересечение всех максимальных по включению барьеров графа <tex>G</tex> равно <tex>A(G)</tex>. | ||
|proof = Пусть <tex>H</tex> {{---}} пересечение всех максимальных по включению барьеров графа <tex>G</tex>. Чтобы доказать теорему, докажем, что <tex>A(G)\subset H</tex> и <tex>A(G)\supset H</tex>.<br> | |proof = Пусть <tex>H</tex> {{---}} пересечение всех максимальных по включению барьеров графа <tex>G</tex>. Чтобы доказать теорему, докажем, что <tex>A(G)\subset H</tex> и <tex>A(G)\supset H</tex>.<br> | ||
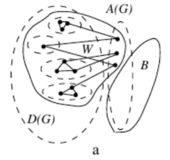
| + | [[Файл: Max_barriers_a.png|170px|thumb|right|Рисунок <tex>1</tex>]] | ||
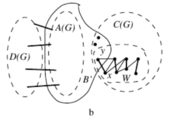
| + | [[Файл: Max_barriers_b.png|170px|thumb|right|Рисунок <tex>2</tex>]] | ||
<br> | <br> | ||
| − | <tex>A(G)\subset H</tex><br> | + | <tex>A(G)\subset H</tex>:<br> |
Пусть <tex>B</tex> {{---}} максимальный по включению барьер, <tex>|A(G)\setminus B| = k > 0</tex>, <tex>B' = B \cup A(G) \Rightarrow |B'| = |B| + k</tex>.<br> | Пусть <tex>B</tex> {{---}} максимальный по включению барьер, <tex>|A(G)\setminus B| = k > 0</tex>, <tex>B' = B \cup A(G) \Rightarrow |B'| = |B| + k</tex>.<br> | ||
Докажем, что <tex>B'</tex> {{---}} барьер и получим противоречие. Для этого достаточно доказать, что <tex>\mathrm{odd}(G\setminus B')\ \geqslant \mathrm{odd}(G\setminus B)\ + k</tex>, ведь в таком случае <tex>\mathrm{odd}(G\setminus B')\ \geqslant \mathrm{def}(G)\ + |B| + k \Rightarrow \mathrm{odd}(G\setminus B')\ - |B'| \geqslant \mathrm{def}(G)</tex>. <br> | Докажем, что <tex>B'</tex> {{---}} барьер и получим противоречие. Для этого достаточно доказать, что <tex>\mathrm{odd}(G\setminus B')\ \geqslant \mathrm{odd}(G\setminus B)\ + k</tex>, ведь в таком случае <tex>\mathrm{odd}(G\setminus B')\ \geqslant \mathrm{def}(G)\ + |B| + k \Rightarrow \mathrm{odd}(G\setminus B')\ - |B'| \geqslant \mathrm{def}(G)</tex>. <br> | ||
| − | + | Пусть <tex>W</tex> {{---}} компонента связности графа <tex>G - B</tex>, содержащая <tex>t > 0</tex> вершин из <tex>A(G)</tex> (см. рисунок <tex>1</tex>), если такой компоненты нет, то <tex>k = 0</tex> {{---}} противоречие. <br> | |
| − | + | В силу [[ Декомпозиция Эдмондса-Галлаи#barier_struct1| леммы о связи барьера]] с <tex>D(G)</tex>, <tex>B\cap D(G) = \varnothing \Rightarrow B'\cap D(G) = \varnothing</tex>. Поэтому, <tex>W</tex> содержит все компоненты связности графа <tex>G(D(G))</tex>, соединённые рёбрами с <tex>W\cap A(G)</tex>. <br> | |
| − | Пусть <tex>W</tex> {{---}} компонента связности графа <tex>G - B</tex>, содержащая <tex>t > 0</tex> вершин из <tex>A(G)</tex> (см. рисунок <tex>1</tex>). <br> | ||
| − | В силу [[ Декомпозиция Эдмондса-Галлаи#barier_struct1| леммы о связи барьера]] с <tex>D(G)</tex>, <tex>B'\cap D(G) = \varnothing</tex>. Поэтому, <tex>W</tex> содержит все компоненты связности графа <tex>G(D(G))</tex>, соединённые рёбрами с <tex>W\cap A(G)</tex>. <br> | ||
По [[ Декомпозиция Эдмондса-Галлаи#theorem_Gallai_Edmonds| теореме Эдмондса-Галлаи]] все эти компоненты связности нечетные и их хотя бы <tex>t + 1</tex>. <br> | По [[ Декомпозиция Эдмондса-Галлаи#theorem_Gallai_Edmonds| теореме Эдмондса-Галлаи]] все эти компоненты связности нечетные и их хотя бы <tex>t + 1</tex>. <br> | ||
| − | Таким образом, при добавлении <tex>t</tex> вершин из <tex>W\cap A(G)</tex> в барьер может исчезнуть одна нечётная компонента связности (если <tex>|W|</tex> нечётно), а появляется хотя бы <tex>t + 1</tex> | + | Таким образом, при добавлении <tex>t</tex> вершин из <tex>W\cap A(G)</tex> в барьер может исчезнуть одна нечётная компонента связности (если <tex>|W|</tex> нечётно), а появляется хотя бы <tex>t + 1</tex> нечётных компонент связности. <br> |
Просуммировав прибавления по всем компонентам связности графа <tex>G - B</tex>, содержащим вершины из <tex>A(G)</tex>, мы получим, что <tex>\mathrm{odd}(G\setminus B')\ \geqslant \mathrm{odd}(G\setminus B)\ + k</tex>, что и требовалось доказать.<br> | Просуммировав прибавления по всем компонентам связности графа <tex>G - B</tex>, содержащим вершины из <tex>A(G)</tex>, мы получим, что <tex>\mathrm{odd}(G\setminus B')\ \geqslant \mathrm{odd}(G\setminus B)\ + k</tex>, что и требовалось доказать.<br> | ||
<br> | <br> | ||
| − | <tex>A(G)\supset H</tex><br> | + | <tex>A(G)\supset H</tex>:<br> |
Предположим противное: пусть существует вершина <tex>x\notin A(G)</tex>, принадлежащая всем максимальным барьерам. По [[ Декомпозиция Эдмондса-Галлаи#barier_struct3| теореме о структуре барьера]] <tex>x\in C(G)</tex>.<br> | Предположим противное: пусть существует вершина <tex>x\notin A(G)</tex>, принадлежащая всем максимальным барьерам. По [[ Декомпозиция Эдмондса-Галлаи#barier_struct3| теореме о структуре барьера]] <tex>x\in C(G)</tex>.<br> | ||
Рассмотрим максимальное паросочетание <tex>M</tex> графа <tex>G</tex>, пусть <tex>xy\in M</tex>.<br> | Рассмотрим максимальное паросочетание <tex>M</tex> графа <tex>G</tex>, пусть <tex>xy\in M</tex>.<br> | ||
Текущая версия на 19:27, 4 сентября 2022
| Теорема: |
Пересечение всех максимальных по включению барьеров графа равно . |
| Доказательство: |
|
Пусть — пересечение всех максимальных по включению барьеров графа . Чтобы доказать теорему, докажем, что и .
|
См. также
- Декомпозиция Эдмондса-Галлаи
- Лапы и минимальные по включению барьеры в графе
- Паросочетания: основные определения, теорема о максимальном паросочетании и дополняющих цепях
- Теорема Татта о существовании полного паросочетания
Источники информации
- Карпов Д. В. — Теория графов, стр 54-55