Централизованный алгоритм для WCP — различия между версиями
(Новая страница: «Категория: Параллельное программирование '''Централизованный алгоритм для WCP''' -- алгор…») |
м (rollbackEdits.php mass rollback) |
||
| (не показано 16 промежуточных версий 6 участников) | |||
| Строка 1: | Строка 1: | ||
[[Категория: Параллельное программирование]] | [[Категория: Параллельное программирование]] | ||
| − | '''Централизованный алгоритм для WCP''' | + | '''Централизованный алгоритм для WCP''' – алгоритм для поиска наименьшего (проще говоря, самого левого) [[Срез, согласованный срез|согласованного среза]] в котором выполняется [[Слабый конъюнктивный предикат (WCP)|слабый конъюнктивный предикат]]. |
| + | Если есть хотя бы один согласованный срез, в котором выполняется слабый конъюнктивный предикат, то такой срез существует и единственен (см. [[слабый конъюнктивный предикат]]). | ||
| + | |||
| + | В централизованном алгоритме используются [[Векторные часы|векторные часы]]. Срез задается набором векторных часов для всех процессов или просто вектором, в котором соответствующая компонента показывает время для соответствующего потока. | ||
| + | |||
| + | Суть алгоритма: | ||
| + | * Есть один процесс-координатор, ответственный за поиск согласованного среза. | ||
| + | * Остальные процессы обычные, их задача — проверять свои локальные предикаты. | ||
| + | * Всякий раз, когда впервые с момента последнего отправленного сообщения локальный предикат становится true, оповещаем об этом координатора, указывая свое векторное время (впервые — чтобы не спамить, состояния процесса между посылками сообщений для системы неотличимы). Векторное время при этом увеличивается. | ||
| + | ** Из этого следует, что если есть наименьший согласованный срез, в котором слабый конъюнктивный предикат верен, то в нём векторные часы всех потоков попарно несравнимы. | ||
| + | ** Более того: если у нас есть срез (необязательно согласованный), в котором все векторные часы всех потоков попарно несравнимы, то он согласован (см. [[Срез, согласованный срез|согласованный срез]]). | ||
| + | ** Таким образом нам достаточно искать наименьший срез из событий, в которых выполняется локальный предикат, а все векторные часы попарно несравнимы. | ||
| + | * Координатор поддерживает в памяти срез-кандидат и очередь необработанных сообщений от каждого процесса. Инвариант: все срезы, у которых хотя бы одна компонента меньше нашего среза-кандидата, гарантированно не подходят. | ||
| + | * Координатор хранит вектора среза-кандидата и флажок для каждой его компоненты: красный – это событие не может быть последним для данного процесса в срезе-кандидате (т.е. нет согласованного среда с верным предикатом, в котором в данном процессе в срез взяты события до данного или раньше), зеленый – может. | ||
| + | * Начальное состояние – все по нулям, красные; | ||
| + | * Обрабатываем приходящие сообщения только от красных процессов, сообщения от зеленых ставим в очередь. | ||
| + | ** Пришедший от красного процесса вектор гарантированно попадает в срез-кандидат. | ||
| + | ** Сравниваем пришедший вектор попарно с другими процессами. Если новый вектор больше, то делаем меньший процесс красным, потому что новый вектор гарантированно попадает, а тогда после меньшего вектора должно идти что-то ещё (иначе не получим попарно несравнимые события). | ||
| + | ** После обработки сообщения делаем бывший красный процесс зеленым. | ||
| + | * Если все зеленое, то мы нашли согласованный срез. | ||
| + | |||
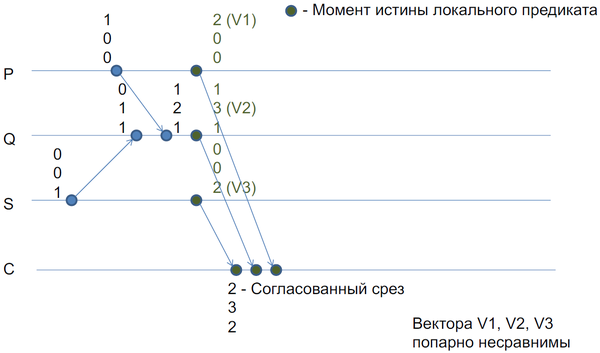
| + | Пример с найденным согласованным срезом, тут координатор по очереди сделал зелёными все процессы: | ||
| + | |||
| + | [[Файл:wcp-search-central-good.png|600px]] | ||
| + | |||
| + | |||
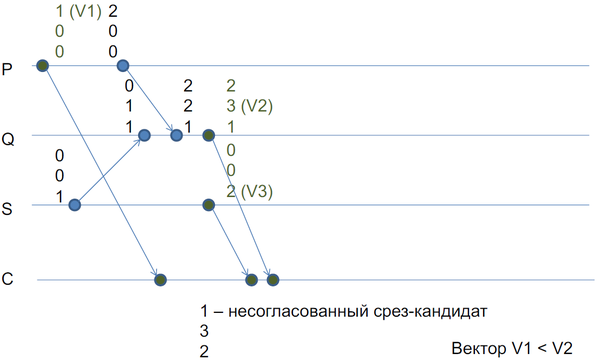
| + | Пример с не найденным согласованным срезом, тут координатор сначала сделал зелёным $P$, потом сделал зелёным $S$, а потом получил мажорирующий их вектор от $Q$ и сделал всех красными, кроме $Q$: | ||
| + | |||
| + | [[Файл:wcp-search-central-bad.png|600px]] | ||
| + | |||
| + | Итого центральному координатору требуется $O(N^2m)$ времени и памяти в сумме ($N$ — количество процессов, $m$ — количество сообщений от одного процесса). | ||
| + | Всего сообщений на алгоритм — $O(Nm)$. | ||
| + | |||
| + | == Оптимизации == | ||
| + | === Уменьшение количества посылок о выполнении предиката === | ||
| + | Если в каком-то процессе выполнялся предикат, а потом он получил сообщение, то не надо ещё раз высылать сообщение координатору. | ||
| + | Доказательство: если бы было решение, где новое состояние процесса после получения сообщения было границей искомого среза, то мы можем сдвинуть это состояние назад. Предикат всё ещё будет выполняться, а срез менее согласованным не станет, т.к. получения сообщений можно выкидывать безболезненно. | ||
| + | |||
| + | На лекции, впрочем, говорилось, что не надо посылать даже если мы просто получили сообщение и предикат стал выполняться. | ||
| + | |||
| + | === Часы с прямой зависимостью вместо векторных === | ||
| + | Если ''каждый'' процесс участвует в вычислении предиката, то нам хватает [[Часы с прямой зависимостью|часов с прямой зависимостью]] вместо векторных. | ||
| + | |||
| + | Смысл в том, чтобы все процессы, которые хоть как-то влияют на предикат, общались напрямую с координатором. | ||
| + | |||
| + | Доказательство: TODO (на лекции не было). | ||
Текущая версия на 19:27, 4 сентября 2022
Централизованный алгоритм для WCP – алгоритм для поиска наименьшего (проще говоря, самого левого) согласованного среза в котором выполняется слабый конъюнктивный предикат. Если есть хотя бы один согласованный срез, в котором выполняется слабый конъюнктивный предикат, то такой срез существует и единственен (см. слабый конъюнктивный предикат).
В централизованном алгоритме используются векторные часы. Срез задается набором векторных часов для всех процессов или просто вектором, в котором соответствующая компонента показывает время для соответствующего потока.
Суть алгоритма:
- Есть один процесс-координатор, ответственный за поиск согласованного среза.
- Остальные процессы обычные, их задача — проверять свои локальные предикаты.
- Всякий раз, когда впервые с момента последнего отправленного сообщения локальный предикат становится true, оповещаем об этом координатора, указывая свое векторное время (впервые — чтобы не спамить, состояния процесса между посылками сообщений для системы неотличимы). Векторное время при этом увеличивается.
- Из этого следует, что если есть наименьший согласованный срез, в котором слабый конъюнктивный предикат верен, то в нём векторные часы всех потоков попарно несравнимы.
- Более того: если у нас есть срез (необязательно согласованный), в котором все векторные часы всех потоков попарно несравнимы, то он согласован (см. согласованный срез).
- Таким образом нам достаточно искать наименьший срез из событий, в которых выполняется локальный предикат, а все векторные часы попарно несравнимы.
- Координатор поддерживает в памяти срез-кандидат и очередь необработанных сообщений от каждого процесса. Инвариант: все срезы, у которых хотя бы одна компонента меньше нашего среза-кандидата, гарантированно не подходят.
- Координатор хранит вектора среза-кандидата и флажок для каждой его компоненты: красный – это событие не может быть последним для данного процесса в срезе-кандидате (т.е. нет согласованного среда с верным предикатом, в котором в данном процессе в срез взяты события до данного или раньше), зеленый – может.
- Начальное состояние – все по нулям, красные;
- Обрабатываем приходящие сообщения только от красных процессов, сообщения от зеленых ставим в очередь.
- Пришедший от красного процесса вектор гарантированно попадает в срез-кандидат.
- Сравниваем пришедший вектор попарно с другими процессами. Если новый вектор больше, то делаем меньший процесс красным, потому что новый вектор гарантированно попадает, а тогда после меньшего вектора должно идти что-то ещё (иначе не получим попарно несравнимые события).
- После обработки сообщения делаем бывший красный процесс зеленым.
- Если все зеленое, то мы нашли согласованный срез.
Пример с найденным согласованным срезом, тут координатор по очереди сделал зелёными все процессы:
Пример с не найденным согласованным срезом, тут координатор сначала сделал зелёным $P$, потом сделал зелёным $S$, а потом получил мажорирующий их вектор от $Q$ и сделал всех красными, кроме $Q$:
Итого центральному координатору требуется $O(N^2m)$ времени и памяти в сумме ($N$ — количество процессов, $m$ — количество сообщений от одного процесса). Всего сообщений на алгоритм — $O(Nm)$.
Оптимизации
Уменьшение количества посылок о выполнении предиката
Если в каком-то процессе выполнялся предикат, а потом он получил сообщение, то не надо ещё раз высылать сообщение координатору. Доказательство: если бы было решение, где новое состояние процесса после получения сообщения было границей искомого среза, то мы можем сдвинуть это состояние назад. Предикат всё ещё будет выполняться, а срез менее согласованным не станет, т.к. получения сообщений можно выкидывать безболезненно.
На лекции, впрочем, говорилось, что не надо посылать даже если мы просто получили сообщение и предикат стал выполняться.
Часы с прямой зависимостью вместо векторных
Если каждый процесс участвует в вычислении предиката, то нам хватает часов с прямой зависимостью вместо векторных.
Смысл в том, чтобы все процессы, которые хоть как-то влияют на предикат, общались напрямую с координатором.
Доказательство: TODO (на лекции не было).