Замкнутость регулярных языков относительно различных операций — различия между версиями
MikhailOK (обсуждение | вклад) (→Основные операции) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 22 промежуточные версии 7 участников) | |||
| Строка 1: | Строка 1: | ||
| − | == | + | == Теорема == |
| − | Пусть <tex>L_1, L_2</tex> - регулярные языки над одним алфавитом <tex>\Sigma</tex>. Тогда следующие языки также являются регулярными: | + | {{Теорема |
| − | #<tex>L_1 \cup L_2</tex> | + | |statement= |
| − | #<tex>L_1 L_2</tex> | + | Пусть <tex>L_1, L_2</tex> {{---}} [[Регулярные языки: два определения и их эквивалентность|регулярные языки]] над одним алфавитом <tex>\Sigma</tex>. Тогда следующие языки также являются регулярными: |
| − | #<tex>L_1^*</tex> | + | #Языки, полученные путём применения следующих теоретико-множественных операций: |
| − | #<tex>\overline{L_1}</tex> | + | #*<tex>L_1 \cup L_2</tex>, |
| − | #<tex>L_1 \cap L_2</tex> | + | #*<tex>\overline{L_1}</tex>, |
| − | #<tex>L_1 \setminus L_2</tex> | + | #*<tex>L_1 \cap L_2</tex>, |
| − | #<tex>\overset{\leftarrow}{L_1}</tex> | + | #*<tex>L_1 \setminus L_2</tex>; |
| − | === | + | #<tex>L_1^*</tex>; |
| − | + | #<tex>L_1 L_2</tex>; | |
| + | #<tex>\overset{\leftarrow}{L_1}</tex>. | ||
| + | |proof= | ||
| + | Как известно, [[Теорема Клини (совпадение классов автоматных и регулярных языков|классы регулярных и автоматных языков совпадают]]. Пусть языки <tex>L_1</tex> и <tex>L_2</tex> распознаются автоматами <tex>A_1 = \langle \Sigma , Q_1 , s_1 , T_1 , \delta_1 : Q_1 \times \Sigma \rightarrow 2^{Q_1} \rangle </tex> и <tex>A_2 = \langle \Sigma , Q_2 , s_2 , T_2 , \delta_2 : Q_2 \times \Sigma \rightarrow 2^{Q_2} \rangle </tex> соответственно. | ||
| + | # | ||
| + | #*<tex>L_1 \cup L_2</tex> является регулярным по определению [[Регулярные языки: два определения и их эквивалентность|регулярных языков]]. | ||
| + | #*Рассмотрим автомат <tex>A_1' = \langle \Sigma , Q_1 , s_1 , Q_1 \setminus T_1 , \delta_1 \rangle </tex>, то есть автомат <tex>A</tex>, в котором терминальные и нетерминальные состояния инвертированы (при таком построении следует помнить, что если в исходном автомате было опущено дьявольское состояние, его нужно явно добавить и сделать допускающим.) Очевидно, он допускает те и только те слова, которые не допускает автомат <tex>A_1</tex>, а значит, задаёт язык <tex>\overline{L_1}</tex>. Таким образом, <tex>\overline{L_1}</tex> {{---}} регулярный. | ||
| + | #*<tex>L_1 \cap L_2 = \overline{\overline{L_1} \cup \overline{L_2}}</tex>. Тогда <tex>L_1 \cap L_2</tex> {{---}} регулярный. Также автомат для пересечения языков можно построить явно, используя конструкцию [[Прямое произведение ДКА|произведения автоматов]]. | ||
| + | #*<tex>L_1 \setminus L_2 = L_1 \cap \overline{L_2}</tex>. Тогда <tex>L_1 \setminus L_2</tex> {{---}} регулярный. | ||
| + | #<tex>L_1^*</tex> является регулярным по определению [[Регулярные языки: два определения и их эквивалентность|регулярных языков]]. | ||
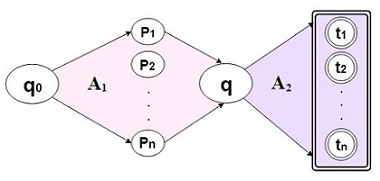
| + | #<tex>L_1 L_2</tex> также является регулярным по определению [[Регулярные языки: два определения и их эквивалентность|регулярных языков]]. | ||
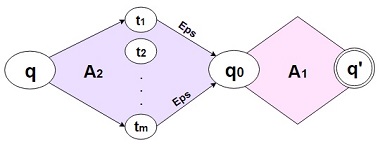
| + | #Рассмотрим [[Автоматы_с_eps-переходами._Eps-замыкание|НКА c <tex>\varepsilon</tex>-переходами]] <tex>A_1' = \langle \Sigma, Q_1, s' , \lbrace s_1 \rbrace, \delta_1' \rangle </tex>, где <tex>\delta_1' (v,c) = \lbrace u | \delta_1(u,c) = v \rbrace </tex>; <tex>\delta_1'(s', \varepsilon) = \lbrace T_i \rbrace</tex>. Если в исходном автомате путь по <tex>\alpha</tex> из <tex>s_1</tex> приводил в терминальное состояние, то в новом автомате существует путь по <tex>\alpha</tex> из этого терминального состояния в <tex>s_1</tex> (и наоборот). Следовательно, этот автомат распознает в точности развернутые слова языка <tex>L_1</tex>. Тогда язык <tex>\overset{\leftarrow}{L_1}</tex> {{---}} регулярный. | ||
| + | }} | ||
| + | == Примеры доказательств == | ||
| + | === Гомоморфизм цепочек === | ||
| + | {{Утверждение | ||
| + | |id=st1 | ||
| + | |statement= | ||
| + | <tex>L \subset \Sigma_1^*</tex> {{---}} регулярный , <tex>\varphi:\Sigma_1^* \rightarrow \Sigma_2^* </tex> {{---}} [[Основные определения: алфавит, слово, язык, конкатенация, свободный моноид слов; операции над языками#Гомоморфизм_языков | гомоморфизм цепочек]]. Тогда <tex>\varphi(L)</tex> {{---}} регулярный. | ||
| + | |proof= | ||
| + | Рассмотрим [[Детерминированные_конечные_автоматы|ДКА]], распознающий <tex>L</tex>. Заменим в нем все переходы по символам на переходы по их образам при гомоморфизме. Полученный автомат (с переходами по строкам) распознает в точности <tex>\varphi(L)</tex> и [[Автоматы_с_eps-переходами._Eps-замыкание|имеет эквивалентный ДКА]]. | ||
| + | }} | ||
| + | {{Утверждение | ||
| + | |id=st2 | ||
| + | |statement= | ||
| + | <tex>L \subset \Sigma_2^*</tex> {{---}} регулярный , <tex>\varphi:\Sigma_1^* \rightarrow \Sigma_2^* </tex> {{---}} [[Основные определения: алфавит, слово, язык, конкатенация, свободный моноид слов; операции над языками#Гомоморфизм_языков | гомоморфизм цепочек]]. Тогда <tex>\varphi^{-1}(L)</tex> {{---}} регулярный. | ||
| + | |proof= | ||
| + | Рассмотрим [[Детерминированные_конечные_автоматы|ДКА]], распознающий <tex>L</tex>. Отследим для каждого состояния <tex>u</tex> и символа <tex>c</tex> строку <tex>\varphi(c)</tex>: <tex> \langle u,\varphi(c) \rangle \vdash^* \langle v,\varepsilon \rangle</tex> и положим <tex>\delta (u,c) = v</tex> в новом автомате (на том же множестве состояний). Автомат с построенной таким образом функцией переходов, очевидно, распознает слова языка <tex>\varphi^{-1}(L)</tex> и только их. | ||
| + | }} | ||
| + | === Язык half(L) === | ||
| + | {{Определение | ||
| + | |definition = Определим <tex>\mathrm{half(L)}</tex> как множество первых половин цепочек языка <tex>L</tex>, то есть множество <tex>\{ w \mid \exists x : wx \in L \land |w| = |x| \}</tex>. }} | ||
| + | Например, если <tex>L = \{ \varepsilon, 0010, 011, 010110 \}</tex>, то <tex>\mathrm{half(L)} = \{ \varepsilon, 00, 010 \}</tex>. Заметим, что цепочки нечетной длины не влияют на <tex>\mathrm{half(L)}</tex>. | ||
| − | + | {{Утверждение | |
| + | |id = st3 | ||
| + | |statement = | ||
| + | Пусть <tex>L</tex> {{---}} [[Регулярные языки: два определения и их эквивалентность|регулярный язык]]. Тогда язык <tex>\mathrm{half(L)}</tex> также регулярен. | ||
| + | |proof = | ||
| + | Так как <tex>L</tex> {{---}} регулярный язык, то существует ДКА <tex>M = \langle \Sigma , Q , q_0 , F , \delta \rangle </tex>, допускающий его. Рассмотрим строку <tex>x</tex>. Для того, чтобы проверить, что <tex>x \in \mathrm{half(L)}</tex>, нам надо убедиться, что существует строка <tex>y</tex> такой же длины, что и <tex>x</tex>, которая, будучи сконкатенированной с <tex>x</tex>, даст строку из <tex>L</tex>, то есть если на вход автомату подать <tex>xy</tex>, то в конце обработки мы окажемся в терминальном состоянии. Предположим, что автомат, закончив обработку <tex>x</tex>, находится в состоянии <tex>q_i</tex>, то есть <tex>\delta(q_0, x) = q_i</tex>. Мы должны проверить, что существует строка <tex>y, |y| = |x|,</tex> которая ведет из состояния <tex>q_i</tex> до какого-нибудь терминального состояния <tex>M</tex>, то есть <tex>\delta(q_i, y) \in F</tex>. | ||
| − | < | + | Предположим, что мы прошли <tex>n</tex> вершин автомата, то есть <tex>|x| = n</tex>. Обозначим за <tex>S_n</tex> множество всех состояний, с которых можно попасть в терминальные за <tex>n</tex> шагов. Тогда <tex>q_i \in S_n \Leftrightarrow x \in \mathrm{half(L)}</tex>. Если мы сможем отслеживать <tex>S_n</tex> и <tex>q_i</tex>, то сможем определять, верно ли, что <tex>x \in \mathrm{half(L)}</tex>. Заметим, что <tex>S_0 \equiv F</tex>. Очевидно мы можем построить <tex>S_{n+1}</tex> зная <tex>S_n</tex> и <tex>\delta</tex>: <tex>S_{n+1} = prev(S_n) = \{ q \in Q \mid \exists a \in \Sigma, q' \in S_n, \delta(q, a) = q' \}</tex> {{---}} множество состояний, из которых есть переход в какое-либо состояние из <tex>S_n</tex> (по единственному символу). Теперь надо найти способ отслеживать и обновлять <tex>S_n</tex>. |
| − | < | ||
| − | |||
| − | < | ||
| − | |||
| − | </ | ||
| − | < | + | Построим ДКА <tex>M'</tex>, который будет хранить эту информацию в своих состояниях. Определим <tex>Q' = Q \times 2^Q</tex>, то есть каждое состояние <tex>M'</tex> {{---}} это пара из одиночного состояния из <tex>M</tex> и множества состояний из <tex>M</tex>. Функцию перехода <tex>\delta'</tex> автомата <tex>M'</tex> определим так, чтобы если по какой-то строке <tex>x</tex> длины <tex>n</tex> в автомате <tex>M</tex> мы перешли в состояние <tex>q_i</tex>, то по этой же строке в автомате <tex>M'</tex> мы перейдем в состояние <tex>(q_i, S_n)</tex>, где <tex>S_n</tex> {{---}} множество состояний из <tex>M</tex>, определенное выше. Вспомним приведенную выше функцию <tex>prev(S_n) = S_{n+1}</tex>. С ее помощью мы можем определить функцию перехода следующим образом: <tex>\delta'((q, S), a) = (\delta(q, a), prev(S))</tex>. Начальное состояние <tex>q_0' = (q_0, S_0) = (q_0, F)</tex>. Множество терминальных состояний {{---}} <tex>F' = \{ (q, S) \mid q \in S, S \in 2^Q \}</tex>. |
| − | |||
| − | + | Теперь по индукции не сложно доказать, что <tex>\delta'(q_0', x) = (\delta(q_0, x), S_n)</tex>, где <tex>|x| = n</tex>. По определению множества терминальных вершин, автомат <tex>M'</tex> допускает строку <tex>x</tex> тогда и только тогда, когда <tex>\delta(q_0, x) \in S_n</tex>. Следовательно, автомат <tex>M'</tex> допускает язык <tex>\mathrm{half(L)}</tex>.Таким образом, мы построили ДКА, который допускает язык <tex>\mathrm{half(L)}</tex>. Следовательно, данный язык является регулярным. | |
| + | }} | ||
| + | === Язык cycle(L) === | ||
| + | {{Определение | ||
| + | |definition = Определим <tex>\mathrm{cycle(L)}</tex> как множество <tex>\{ w \mid </tex> цепочку <tex>w</tex> можно представить в виде <tex>w = xy</tex>, где <tex>yx \in L \}</tex>. }} | ||
| + | Например, если <tex>L = \{ 01, 011 \}</tex>, то <tex>\mathrm{cycle(L)} = \{ 01, 10, 011, 110, 101 \}</tex>. | ||
| − | <tex> | + | {{Утверждение |
| + | |id = st5 | ||
| + | |statement = | ||
| + | Пусть <tex>L</tex> {{---}} [[Регулярные языки: два определения и их эквивалентность|регулярный язык]]. Тогда язык <tex>\mathrm{cycle(L)}</tex> также регулярен. | ||
| + | |proof = | ||
| + | [[Файл:Enfa_before.jpg|right|thumb|380px|Рис. 1. Разбиение автомата.]] | ||
| + | [[Файл:Enfa-after.jpg|right|thumb|380px|Рис. 2. Перестроение.]] | ||
| + | Так как <tex>L</tex> {{---}} регулярный язык, то существует допускающий его ДКА <tex>M = \langle \Sigma , Q , q_0 , F , \delta \rangle </tex>. Построим из <tex>M</tex> [[Автоматы_с_eps-переходами._Eps-замыкание|недетерминированный автомат с <tex>\varepsilon</tex>-переходами]] следующим образом: рассмотрим состояние <tex>q \in Q</tex>, из которого есть переходы в другие состояния (то есть начиная с <tex>q</tex> можно построить непустое слово, заканчивающееся в терминальной вершине). Тогда если какое-то слово проходит через это состояние, оно может быть зациклено таким образом, что его суффикс, начинающийся с <tex>q</tex>, станет префиксом нового слова, а префикс, заканчивающийся в <tex>q</tex> {{---}} суффиксом. Разделим автомат на две части <tex>A_1</tex> и <tex>A_2</tex> такие, что <tex>A_1</tex> будет содержать все вершины, из которых достижима <tex>q</tex>, а <tex>A_2</tex> {{---}} все вершины, которые достижимы из <tex>q</tex> (см. рис. 1). Заметим, что каждая вершина может содержаться в обеих частях одновременно, такое может случиться, если автомат <tex>M</tex> содержит циклы. Теперь перестроим автомат так, что он будет принимать слова "зацикленные" вокруг <tex>q</tex>, то есть начинающиеся с <tex>q</tex> и после достижения терминальной вершины продолжающиеся с <tex>q_0</tex> (см. рис. 2). Для этого стартовой вершиной сделаем <tex>q</tex> и построим от нее часть <tex>A_2</tex>. Теперь добавим состояние <tex>q_0</tex> и соединим с ним все терминальные состояния из <tex>A_2</tex> с помощью <tex>\varepsilon</tex>-переходов. Далее построим от <tex>q_0</tex> часть <tex>A_1</tex>. Добавим вершину <tex>q'</tex>, эквивалентную <tex>q</tex>, и сделаем ее терминальной. Данный автомат принимает слова, зацикленные вокруг выбранной вершины <tex>q</tex>. Мы хотим, чтобы автомат принимал слова, зацикленные вокруг любой такой <tex>q</tex>. Для этого создадим новую стартовую вершину <tex>q_0'</tex> и свяжем ее <tex>\varepsilon</tex>-переходами со всеми перестроенными автоматами (зацикленными вокруг всех подходящих <tex>q</tex>), в том числе и с изначальным автоматом. Построенный автомат допускает язык <tex>\mathrm{cycle(L)}</tex>, следовательно, данный язык является регулярным. | ||
| + | }} | ||
| + | [[Файл:Ex_1_before.jpg|left|thumb|260px|Рис. 3. Автомат, принимающий язык <tex>L</tex>.]] | ||
| + | [[Файл:Ex_1_after.jpg|right|thumb|380px|Рис. 4. Автомат, принимающий язык <tex>\mathrm{cycle(L)}</tex>.]] | ||
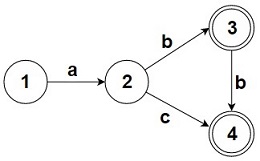
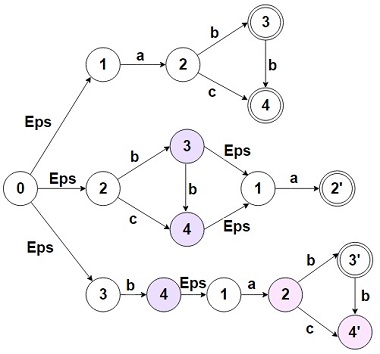
| + | Для лучшего понимания алгоритма перестроения автомата рассмотрим пример. | ||
| − | <tex> | + | На рис. 3 представлен автомат, допускающий язык <tex>L = \{ ab, abb, ac \}</tex>. На рис. 4 показано, как этот автомат был перестроен. Были добавлены части, зацикленные относительно вершин <tex>2</tex> и <tex>3</tex>. Появилась новая стартовая вершина <tex>0</tex>, которая связана <tex>\varepsilon</tex>-переходами с изначальным автоматом и его измененными версиями. Данный автомат распознает язык <tex>\mathrm{cycle(L)} = \{ ab, abb, ac, ba, bba, ca, bab \}</tex>: первые три слова распознает первая часть, которая совпадает с изначальным автоматом; следующие три {{---}} вторая, перестроенная относительно вершины <tex>2</tex>; последнее слово распознает третья часть, зацикленная относительно вершины <tex>3</tex>. |
| − | < | + | <br><br><br><br><br><br><br><br><br><br><br> |
| − | + | === Язык alt(L, M) === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Определение | {{Определение | ||
| − | |definition= | + | |definition = Пусть <tex>w = w_1 w_2 \dots w_n</tex> и <tex>x = x_1 x_2 \dots x_n</tex>. Определим <tex>alternation(w, x) = w_1 x_1 w_2 x_2 \dots w_n x_n</tex>.}} |
| − | }} | + | Теперь распространим это определение: |
{{Определение | {{Определение | ||
| − | |definition= | + | |definition = Пусть <tex>L</tex> и <tex>M</tex> {{---}} два языка над одним алфавитом <tex>\Sigma</tex>. Тогда <tex>\mathrm{alt(L, M)} = \{ alternation(w, x) \mid |w| = |x|, w \in L, x \in M \}</tex>.}} |
| − | + | Например, если <tex>L = \{ 10, 00, 111, 1001 \}</tex> и <tex>M = \{ 11, 0101 \}</tex>, то <tex>\mathrm{alt(L, M)} = \{ 1101, 0101, 10010011 \}</tex>. | |
{{Утверждение | {{Утверждение | ||
| − | |id= | + | |id = st4 |
| − | |statement= | + | |statement = Пусть <tex>L</tex> и <tex>M</tex> {{---}} [[Регулярные языки: два определения и их эквивалентность|регулярные языки]]. Тогда <tex>\mathrm{alt(L, M)}</tex> также является регулярным. |
| − | <tex>L \ | + | |proof = Так как <tex>L</tex> и <tex>M</tex> {{---}} регулярные языки, то существуют ДКА <tex>D_L = \langle \Sigma , Q_L , q_{0L} , F_L, \delta_L \rangle</tex>, распознающий язык <tex>L</tex>, и <tex>D_M = \langle \Sigma , Q_M , q_{0M} , F_M, \delta_M \rangle</tex>, распознающий язык <tex>M</tex>. Построим автомат <tex>D_{alt}</tex>, который будет распознавать язык <tex>\mathrm{alt(L, M)}</tex>. Идея следующая: каждое состояние этого автомата будем описывать тремя значениями <tex>(p, q, b)</tex>, где <tex>p \in Q_L</tex>, <tex>q \in Q_M</tex> и <tex>b \in \{ 1, 0 \}</tex>. Нам нужно организовать чередование переходов по состояниям автоматов, то есть если мы на определенном шаге перешли от одного состояния автомата <tex>D_L</tex> до другого, то на следующем мы обязаны совершить переход по состояниям автомата <tex>D_M</tex>. Для этого нам нужно обновлять состояние одного автомата и при этом сохранять состояние другого для следующего перехода. Тут мы будем использовать третье значение: если <tex>b = 0</tex>, то будет двигаться по состояниям первого автомата, то есть значение <tex>p</tex> при переходе в новое состояние автомата <tex>D_{alt}</tex> поменяется, <tex>q</tex> останется неизменной, <tex>b</tex> станет <tex>1</tex>, если <tex>b = 1</tex>, то, соответственно, все наоборот. То есть у нас будут две функции перехода, выбирать нужную будем в зависимости от четности третьего параметра. Важно, что на каждом шаге мы инвертируем значение <tex>b</tex>, что гарантирует чередование. Определим автомат <tex>D_{alt} = \langle \Sigma, Q', q_0', F', \delta' \rangle</tex> следующим образом: |
| − | + | # <tex>Q' = Q_L \times Q_M \times \{ 0, 1 \}</tex> | |
| − | + | # <tex>q_0' = (q_{0L}, q_{0M}, 0)</tex> | |
| + | # <tex>F' = F_L \times F_M \times \{ 0 \}</tex> | ||
| + | # <tex>\delta'((p, q, 0), a) = (\delta_L(p, a), q, 1)</tex> и <tex>\delta'((p, q, 1), a) = (p, \delta_M(q, a), 0)</tex> | ||
| + | Стартовая вершина имеет третий параметр <tex>b = 0</tex>, так как первое значение должно быть получено из автомата <tex>D_L</tex>. Аналогично все терминальные вершины должны иметь то же значение последнего параметра, так как количество переходов должно быть четным и последний переход должен был быть осуществлен по автомату <tex>D_M</tex>. Функция перехода <tex>\delta'</tex> использует <tex>\delta_L</tex> для получения нечетных символов и <tex>\delta_M</tex> для четных. Таким образом, <tex>D_{alt}</tex> состоит из чередующихся символов <tex>D_L</tex> и <tex>D_M</tex>. При этом <tex>D_{alt}</tex> принимает <tex>w</tex> тогда и только тогда, когда <tex>D_L</tex> последовательно принимает все нечетные символы <tex>w</tex> и <tex>D_M</tex> {{---}} все четные, а так же <tex>w</tex> имеет четную длину. Следовательно, <tex>D_{alt}</tex> распознает язык <tex>\mathrm{alt(L, M)}</tex>, что доказывает, что <tex>\mathrm{alt(L, M)}</tex> является регулярным. | ||
}} | }} | ||
| + | [[Файл:Alt ex 1.jpg|left|thumb|265px|Рис. 5. Автоматы для языков <tex>L</tex> и <tex>M</tex>.]] | ||
| + | [[Файл:Alt ex 2.jpg|right|thumb|390px|Рис. 6. Автомат, принимающий язык <tex>\mathrm{alt(L, M)}</tex>.]] | ||
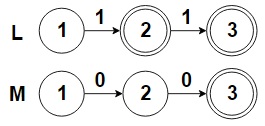
| + | Чтобы более наглядно показать, как строится автомат <tex>D_{alt}</tex>, разберем пример. Пусть <tex>L = \{ 1, 11 \}</tex> и <tex>M = \{ 00 \}</tex> (см. рис. 5). Все состояния нового автомата представлены на рис. 6. Стартовая вершина <tex>q_0' = (1, 1, 0)</tex>, множество терминальных вершин {{---}} <tex>F' = \{ (2, 3, 0), (3, 3, 0) \}</tex>. Мы видим, что построенные по функции <tex>\delta'</tex> переходы на каждом шаге меняют состояние одного из автоматов, а именно того, по которому происходит переход, сохраняя состояние другого для следующего шага. Таким образом, каждый следующий символ получен из автомата, отличного от того, что был использован на предыдущем шаге. Декартово произведение состояний гарантирует, что мы рассмотрим все состояния и переходы изначальных автоматов. Для данного примера мы получаем, что <tex>\mathrm{alt(L, M)} = \{ 1010 \}</tex>. | ||
| − | + | <br><br><br><br><br><br><br> | |
| − | + | ||
| − | + | == См. также == | |
| − | < | + | * [[Анализ свойств регулярных языков (пустота, совпадение, включение, конечность, подсчет числа слов)]] |
| − | + | * [[Теорема Клини (совпадение классов автоматных и регулярных языков)]] | |
| − | + | ||
| − | + | == Источники == | |
| + | * Хопкрофт Д., Мотвани Р., Ульман Д. "Введение в теорию автоматов, языков и вычислений", 2-е изд. : Пер. с англ. — М.:Издательский дом «Вильямс», 2002. {{---}} С. 149 — ISBN 5-8459-0261-4 | ||
| + | [[Категория: Теория формальных языков]] | ||
| + | [[Категория: Автоматы и регулярные языки]] | ||
| + | [[Категория: Свойства конечных автоматов]] | ||
Текущая версия на 19:30, 4 сентября 2022
Содержание
Теорема
| Теорема: |
Пусть — регулярные языки над одним алфавитом . Тогда следующие языки также являются регулярными:
|
| Доказательство: |
|
Как известно, классы регулярных и автоматных языков совпадают. Пусть языки и распознаются автоматами и соответственно.
|
Примеры доказательств
Гомоморфизм цепочек
| Утверждение: |
— регулярный , — гомоморфизм цепочек. Тогда — регулярный. |
| Рассмотрим ДКА, распознающий . Заменим в нем все переходы по символам на переходы по их образам при гомоморфизме. Полученный автомат (с переходами по строкам) распознает в точности и имеет эквивалентный ДКА. |
| Утверждение: |
— регулярный , — гомоморфизм цепочек. Тогда — регулярный. |
| Рассмотрим ДКА, распознающий . Отследим для каждого состояния и символа строку : и положим в новом автомате (на том же множестве состояний). Автомат с построенной таким образом функцией переходов, очевидно, распознает слова языка и только их. |
Язык half(L)
| Определение: |
| Определим как множество первых половин цепочек языка , то есть множество . |
Например, если , то . Заметим, что цепочки нечетной длины не влияют на .
| Утверждение: |
Пусть — регулярный язык. Тогда язык также регулярен. |
|
Так как — регулярный язык, то существует ДКА , допускающий его. Рассмотрим строку . Для того, чтобы проверить, что , нам надо убедиться, что существует строка такой же длины, что и , которая, будучи сконкатенированной с , даст строку из , то есть если на вход автомату подать , то в конце обработки мы окажемся в терминальном состоянии. Предположим, что автомат, закончив обработку , находится в состоянии , то есть . Мы должны проверить, что существует строка которая ведет из состояния до какого-нибудь терминального состояния , то есть . Предположим, что мы прошли вершин автомата, то есть . Обозначим за множество всех состояний, с которых можно попасть в терминальные за шагов. Тогда . Если мы сможем отслеживать и , то сможем определять, верно ли, что . Заметим, что . Очевидно мы можем построить зная и : — множество состояний, из которых есть переход в какое-либо состояние из (по единственному символу). Теперь надо найти способ отслеживать и обновлять . Построим ДКА , который будет хранить эту информацию в своих состояниях. Определим , то есть каждое состояние — это пара из одиночного состояния из и множества состояний из . Функцию перехода автомата определим так, чтобы если по какой-то строке длины в автомате мы перешли в состояние , то по этой же строке в автомате мы перейдем в состояние , где — множество состояний из , определенное выше. Вспомним приведенную выше функцию . С ее помощью мы можем определить функцию перехода следующим образом: . Начальное состояние . Множество терминальных состояний — . Теперь по индукции не сложно доказать, что , где . По определению множества терминальных вершин, автомат допускает строку тогда и только тогда, когда . Следовательно, автомат допускает язык .Таким образом, мы построили ДКА, который допускает язык . Следовательно, данный язык является регулярным. |
Язык cycle(L)
| Определение: |
| Определим как множество цепочку можно представить в виде , где . |
Например, если , то .
| Утверждение: |
Пусть — регулярный язык. Тогда язык также регулярен. |
| Так как — регулярный язык, то существует допускающий его ДКА . Построим из недетерминированный автомат с -переходами следующим образом: рассмотрим состояние , из которого есть переходы в другие состояния (то есть начиная с можно построить непустое слово, заканчивающееся в терминальной вершине). Тогда если какое-то слово проходит через это состояние, оно может быть зациклено таким образом, что его суффикс, начинающийся с , станет префиксом нового слова, а префикс, заканчивающийся в — суффиксом. Разделим автомат на две части и такие, что будет содержать все вершины, из которых достижима , а — все вершины, которые достижимы из (см. рис. 1). Заметим, что каждая вершина может содержаться в обеих частях одновременно, такое может случиться, если автомат содержит циклы. Теперь перестроим автомат так, что он будет принимать слова "зацикленные" вокруг , то есть начинающиеся с и после достижения терминальной вершины продолжающиеся с (см. рис. 2). Для этого стартовой вершиной сделаем и построим от нее часть . Теперь добавим состояние и соединим с ним все терминальные состояния из с помощью -переходов. Далее построим от часть . Добавим вершину , эквивалентную , и сделаем ее терминальной. Данный автомат принимает слова, зацикленные вокруг выбранной вершины . Мы хотим, чтобы автомат принимал слова, зацикленные вокруг любой такой . Для этого создадим новую стартовую вершину и свяжем ее -переходами со всеми перестроенными автоматами (зацикленными вокруг всех подходящих ), в том числе и с изначальным автоматом. Построенный автомат допускает язык , следовательно, данный язык является регулярным. |
Для лучшего понимания алгоритма перестроения автомата рассмотрим пример.
На рис. 3 представлен автомат, допускающий язык . На рис. 4 показано, как этот автомат был перестроен. Были добавлены части, зацикленные относительно вершин и . Появилась новая стартовая вершина , которая связана -переходами с изначальным автоматом и его измененными версиями. Данный автомат распознает язык : первые три слова распознает первая часть, которая совпадает с изначальным автоматом; следующие три — вторая, перестроенная относительно вершины ; последнее слово распознает третья часть, зацикленная относительно вершины .
Язык alt(L, M)
| Определение: |
| Пусть и . Определим . |
Теперь распространим это определение:
| Определение: |
| Пусть и — два языка над одним алфавитом . Тогда . |
Например, если и , то .
| Утверждение: |
Пусть и — регулярные языки. Тогда также является регулярным. |
|
Так как и — регулярные языки, то существуют ДКА , распознающий язык , и , распознающий язык . Построим автомат , который будет распознавать язык . Идея следующая: каждое состояние этого автомата будем описывать тремя значениями , где , и . Нам нужно организовать чередование переходов по состояниям автоматов, то есть если мы на определенном шаге перешли от одного состояния автомата до другого, то на следующем мы обязаны совершить переход по состояниям автомата . Для этого нам нужно обновлять состояние одного автомата и при этом сохранять состояние другого для следующего перехода. Тут мы будем использовать третье значение: если , то будет двигаться по состояниям первого автомата, то есть значение при переходе в новое состояние автомата поменяется, останется неизменной, станет , если , то, соответственно, все наоборот. То есть у нас будут две функции перехода, выбирать нужную будем в зависимости от четности третьего параметра. Важно, что на каждом шаге мы инвертируем значение , что гарантирует чередование. Определим автомат следующим образом:
|
Чтобы более наглядно показать, как строится автомат , разберем пример. Пусть и (см. рис. 5). Все состояния нового автомата представлены на рис. 6. Стартовая вершина , множество терминальных вершин — . Мы видим, что построенные по функции переходы на каждом шаге меняют состояние одного из автоматов, а именно того, по которому происходит переход, сохраняя состояние другого для следующего шага. Таким образом, каждый следующий символ получен из автомата, отличного от того, что был использован на предыдущем шаге. Декартово произведение состояний гарантирует, что мы рассмотрим все состояния и переходы изначальных автоматов. Для данного примера мы получаем, что .
См. также
- Анализ свойств регулярных языков (пустота, совпадение, включение, конечность, подсчет числа слов)
- Теорема Клини (совпадение классов автоматных и регулярных языков)
Источники
- Хопкрофт Д., Мотвани Р., Ульман Д. "Введение в теорию автоматов, языков и вычислений", 2-е изд. : Пер. с англ. — М.:Издательский дом «Вильямс», 2002. — С. 149 — ISBN 5-8459-0261-4