Splay-дерево — различия между версиями
(→Время работы) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 3 промежуточные версии 3 участников) | |||
| Строка 32: | Строка 32: | ||
===find(tree, x)=== | ===find(tree, x)=== | ||
| − | Эта операция выполняется как для обычного [[Дерево поиска, наивная реализация|бинарного дерева]], только после нее запускается операция splay. | + | Эта операция выполняется как для обычного [[Дерево поиска, наивная реализация|бинарного дерева поиска]], только после нее запускается операция splay. |
===merge(tree1, tree2)=== | ===merge(tree1, tree2)=== | ||
| Строка 80: | Строка 80: | ||
p(r) = p | p(r) = p | ||
'''if''' (v.right != '''null''') | '''if''' (v.right != '''null''') | ||
| − | p(v) = v | + | p(v.right) = v |
Реализация splay: | Реализация splay: | ||
Текущая версия на 19:30, 4 сентября 2022
Сплей-дерево (англ. Splay-tree) — это двоичное дерево поиска. Оно позволяет находить быстрее те данные, которые использовались недавно. Относится к разряду сливаемых деревьев. Сплей-дерево было придумано Робертом Тарьяном и Даниелем Слейтером в году.
Содержание
Эвристики
Для того, чтобы доступ к недавно найденным данным был быстрее, надо, чтобы эти данные находились ближе к корню. Этого мы можем добиться, используя различные эвристики:
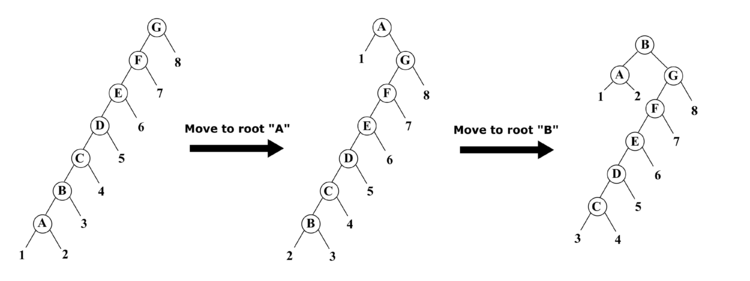
- Move to Root — совершает повороты вокруг ребра , где — найденная вершина, — ее предок, пока не окажется корнем дерева. Однако можно построить такую последовательность операций, что амортизированное время доступа к вершине будет .
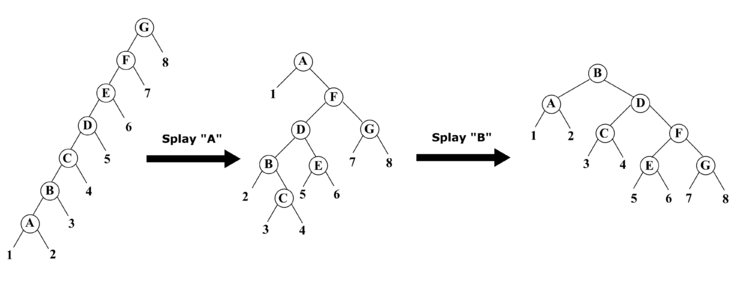
- Splay — также совершает повороты, но чередует различные виды поворотов, благодаря чему достигается логарифмическая амортизированная оценка. Она будет подробно описана ниже.
Пример: При последовательном использовании операций "move to root" для вершин и требуется по поворотов, в то время как при использовании операции "splay" для вершины достаточно поворотов.
Операции со splay-деревом
splay(tree, x)
"splay" делится на случая:
zig
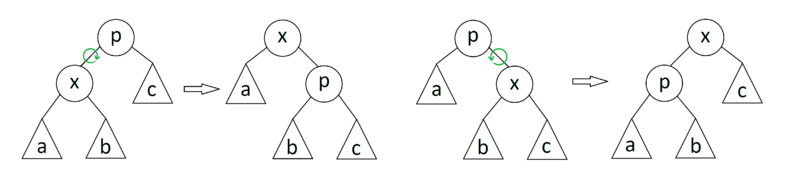
Если — корень дерева с сыном , то совершаем один поворот вокруг ребра , делая корнем дерева. Данный случай является крайним и выполняется только один раз в конце, если изначальная глубина была нечетной.
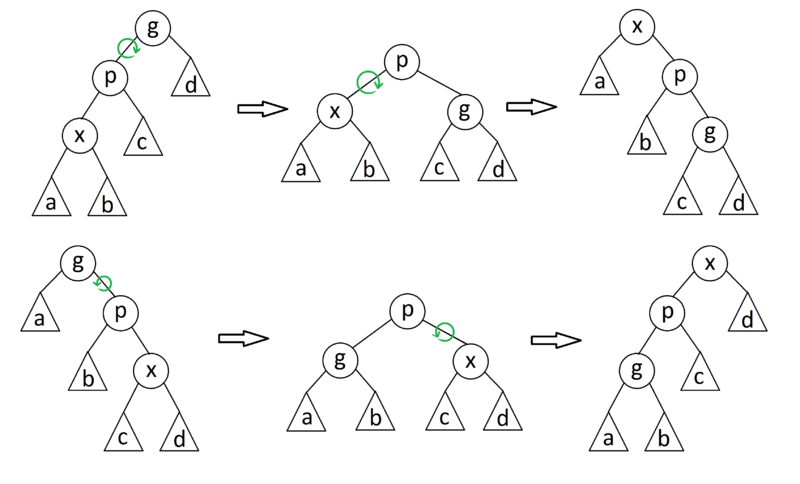
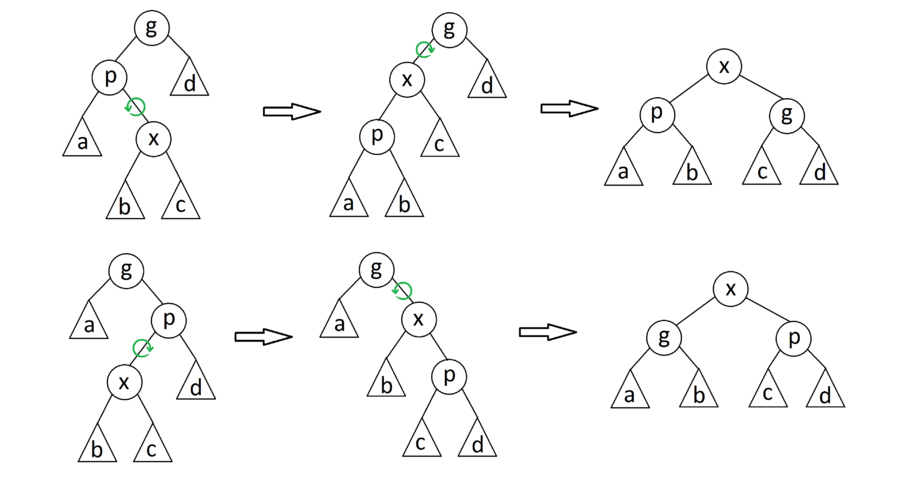
zig-zig
Если — не корень дерева, а и — оба левые или оба правые дети, то делаем поворот ребра , где отец , а затем поворот ребра .
zig-zag
Если — не корень дерева и — левый ребенок, а — правый, или наоборот, то делаем поворот вокруг ребра , а затем поворот нового ребра , где — бывший родитель .
Данная операция занимает времени, где — длина пути от до корня.
find(tree, x)
Эта операция выполняется как для обычного бинарного дерева поиска, только после нее запускается операция splay.
merge(tree1, tree2)
У нас есть два дерева и , причём подразумевается, что все элементы первого дерева меньше элементов второго. Запускаем splay от самого большого элемента в дереве (пусть это элемент ). После этого корень содержит элемент , при этом у него нет правого ребёнка. Делаем правым поддеревом и возвращаем полученное дерево.
split(tree, x)
Запускаем splay от элемента и возвращаем два дерева, полученные отсечением правого или левого поддерева от корня, в зависимости от того, содержит корень элемент больше или не больше, чем .
add(tree, x)
Запускаем split(tree, x), который нам возвращает деревья и , их подвешиваем к как левое и правое поддеревья соответственно.
remove(tree, x)
Запускаем splay от элемента и возвращаем Merge от его детей.
Реализация операции splay
Bottom-up
В этой реализации операция splay производится при подъеме от целевой вершины до корня путем применения поворотов. Для подъема по дереву требуется доступ к вершине-родителю. Этого можно достичь либо путем хранения в каждой вершине ссылки на родителя, либо с помощью стека вершин на пути от корня к целевой.
Определим вспомогательные функции:
- — поворот ребра, соединяющего v и его правого сына
- — симметрично
- — родитель вершины
- — родитель родителя вершины
Приведем реализацию , , . Реализация симметрична. Положим, что для доступа к родительской вершине имеется соответствующее поле.
Node p(Node v): return v.parent
Node g(Node v): return p(p(v))
void rotate_left(Node v):
Node p = p(v)
Node r = v.right
if (p != null)
if (p.left == v)
p.left = r
else
p.right = r
Node tmp = r.left
r.left = v
v.right = tmp
p(v) = r
p(r) = p
if (v.right != null)
p(v.right) = v
Реализация splay:
void splay(Node v):
while (p(v) != null)
if (v == p(v).left)
if (g(v) == null)
rotate_right(p(v))
else if (p(v) == g(v).left)
rotate_right(g(v))
rotate_right(p(v))
else
rotate_right(p(v))
rotate_left(p(v))
else
if (g(v) == null)
rotate_left(p(v))
else if (p(v) == g(v).right)
rotate_left(g(v))
rotate_left(p(v))
else
rotate_left(p(v))
rotate_right(p(v))
Преимуществом данного подхода является возможность инкапсуляции всех модификаций структуры дерева, включая создание вспомогательных переменных и нарушение инвариантов. Рекомендуется для использования в случае, когда есть прямой доступ к целевой для операции splay вершине, иначе требуется два прохода по пути от корня до вершины (первый — поиск вершины стандартным алгоритмом, второй — splay).
Top-down
Данная реализация не требует прямого доступа к целевой вершине, поскольку процесс перебалансировки происходит во время поиска вершины в дереве.
В процессе спуска во время операции splay дерево разбивается на три части: , , . Деревья и содержат все вершины исходного дерева, для которых на данном этапе известно, что они меньше или больше искомого элемента соответственно. Дерево содержит вершины, принадлежащие поддереву текущей вершины на пути к целевой в исходном дереве. Изначально деревья и пусты, а текущая вершина пути к целевой — корень.
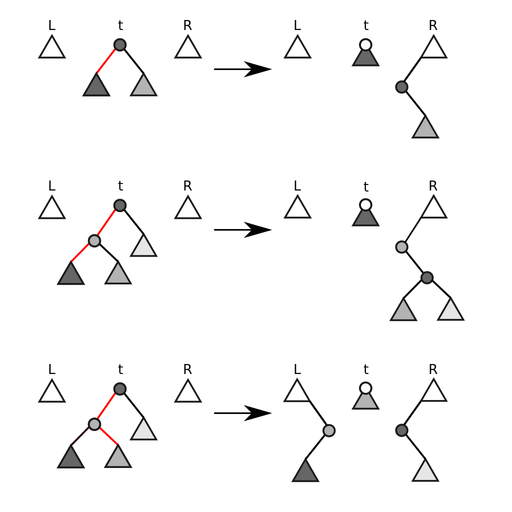
За одну итерацию операции splay производится спуск на две вершины по пути поиска целевой. Пройденные ребра удаляются, и отсоединившиеся при этом поддеревья добавляются правым ребенком наибольшей по значению вершине дерева или левым ребенком к наименьшей по значению вершине дерева . При этом если происходит спуск оба раза в левых или правых детей, то перед присоединением производится поворот.
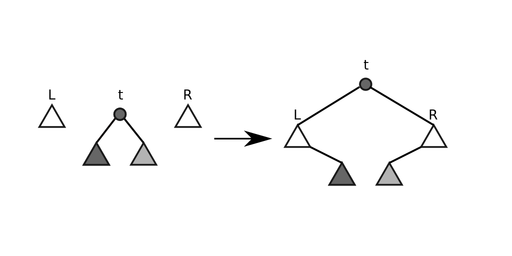
В конце пути производится слияние деревьев , и таким образом, что новым корнем дерева становится вершина с целевым значением.
Приведем реализацию. Определим переменные:
- — значение в целевой вершине
- — текущая вершина, до и после splay — корень дерева
- — наибольшая по значению вершина дерева
- — наименьшая по значению вершина дерева
- — корень дерева
- — корень дерева
Определим вспомогательные функции:
- — поворот ребра, соединяющего и его правого сына
- — симметрично
- — удалить ребро, соединяющее и его правого сына, соединить с полученным деревом
- — симметрично
- — слить деревья , и
Приведем реализацию , , . Реализация и симметрична.
Node rotate_left(Node v): Node r = v.right Note tmp = r.left r.left = v v.right = tmp return r
Node break_left(Node v):
Node tmp = v.right
v.right = null
if (l == null)
l_root = l = v
else
l.right = v
l = v
return tmp
void assemble(): l.right = t.left r.left = t.right t.left = l_root t.right = r_root
Реализация splay:
void splay(Value val):
while (t.value != val)
if (val < t.value)
if (val == t.left.value)
t = break_right(t)
else if (val < t.left.value)
t = rotate_right(t)
t = break_right(t)
else
t = break_right(t)
t = break_left(t)
else
if (val == t.right.value)
t = break_left(t)
else if (val > t.right.value)
t = rotate_left(t)
t = break_left(t)
else
t = break_left(t)
t = break_right(t)
assemble()
Реализацию splay можно упростить, опустив вторую операцию удаления ребра в случае zig-zag. Приведем также ее:
void simplified_splay(Value val):
while (t.value != val)
if (val < t.value)
if (val < t.left.value)
t = rotate_right(t)
t = break_right(t)
else
if (val > t.right.value)
t = rotate_left(t)
t = break_left(t)
assemble()
Время работы
В обеих реализациях осуществляется проход по пути от корня к целевой вершине и/или обратно. По вышеупомянутой Лемме, путь состоит из вершин. Обработка каждой вершины имеет сложность . Таким образом, сложность приведенных выше операции splay —
Анализ операции splay
Амортизационный анализ сплей-дерева проводится с помощью метода потенциалов. Потенциалом рассматриваемого дерева назовём сумму рангов его вершин. Ранг вершины — это величина, обозначаемая и равная , где — количество вершин в поддереве с корнем в .
| Лемма: |
Амортизированное время операции splay вершины в дереве с корнем не превосходит |
| Доказательство: |
|
Проанализируем каждый шаг операции splay. Пусть и — ранги вершин после шага и до него соответственно, — предок вершины , а — предок (если есть). Разберём случаи в зависимости от типа шага: zig. Поскольку выполнен один поворот, то амортизированное время выполнения шага (поскольку только у вершин и меняется ранг). Ранг вершины уменьшился, поэтому . Ранг вершины увеличился, поэтому . Следовательно, . zig-zig. Выполнено два поворота, амортизированное время выполнения шага . Поскольку после поворотов поддерево с корнем в будет содержать все вершины, которые были в поддереве с корнем в (и только их), поэтому . Используя это равенство, получаем: , поскольку . Далее, так как , получаем, что . Мы утверждаем, что эта сумма не превосходит , то есть, что . Преобразуем полученное выражение следующим образом: . Из рисунка видно, что , значит, сумма выражений под логарифмами не превосходит единицы. Далее, рассмотрим сумму логарифмов . При произведение по неравенству между средними не превышает . А поскольку логарифм — функция возрастающая, то , что и является требуемым неравенством. zig-zag. Выполнено два поворота, амортизированное время выполнения шага . Поскольку , то . Далее, так как , то . Мы утверждаем, что эта сумма не превосходит , то есть, что . Но, поскольку - аналогично доказанному ранее, что и требовалось доказать. Итого, получаем, что амортизированное время шага zig-zag не превосходит . Поскольку за время выполнения операции splay выполняется не более одного шага типа zig, то суммарное время не будет превосходить , поскольку утроенные ранги промежуточных вершин сокращаются (входят в сумму как с плюсом, так и с минусом). Тогда суммарное время работы splay , где — число элементов в дереве. |
Статическая оптимальность сплей-дерева
| Теорема: |
Если к ключам , сложенным в сплей-дерево выполняется запросов, к -му ключу осуществляется запросов, где , то суммарное время работы не превышает , где , — шенноновская энтропия |
| Доказательство: |
|
Известно, что — шенноновская энтропия. Пусть — количество вершин в поддереве с корнем в . А — ранг вершины. Обозначим за корень -дерева. Из предыдущей теоремы известно, что Пусть , тогда . |
Теорема о близких запросах в сплей-дереве
| Теорема (о близких запросах в сплей-дереве): |
Пусть в сплей-дерево сложены ключи . Зафиксируем один из ключей . Пусть выполняется запросов к ключам. Тогда суммарное время на запросы есть , где — значение в вершине, к которой обращаются в -ый запрос. |
| Доказательство: |
|
Для доказательства теоремы воспользуемся методом потенциалов: . По условию выполняется запросов, следовательно . Введем следующие обозначения:
Пусть — вес дерева. Тогда . Последнее верно, так как при фиксированном , начиная с некоторого места, а именно , ряд сходится. Из определения размера узла следует, что . Также заметим, что для любого от до верно, что , так как максимальное значение знаменателя в определении достигается при и или наоборот. Тогда, воспользовавшись полученными оценками, найдем изменение потенциала сплей-дерева после запросов: . Первое неравенство верно, так как максимальное значение потенциала достигается при , а минимальное при , а значит изменение потенциала не превышает разности этих величин. Обозначим за корень сплей-дерева. Тогда, воспользовавшись вышеуказанной леммой (можно показать, что она верна для любого фиксированного определения веса узла) получаем, что . Докажем, что данное определение потенциала удовлетворяет условию теоремы о методе потенциалов. Для любого верно, что , так как , и , как было показано выше. Так как количество операций на запрос , то и , где — функция из теоремы о методе потенциалов, равная в данном случае . Следовательно, потенциал удовлетворяет условию теоремы. Тогда, подставляя найденные значения в формулу , получаем, что . |
Данная теорема показывает, что сплей-деревья поддерживают достаточно эффективный доступ к ключам, которые находятся близко к какому-то фиксированному ключу.
Splay-деревья по неявному ключу
Splay-дерево по неявному ключу полностью аналогично декартову дереву по неявному ключу, неявным ключом также будет количество элементов дерева, меньших данного. Аналогично, будем хранить вспомогательную величину — количество вершин в поддереве. К операциям, которые уже были представлены в декартовом дереве, добавляется splay, но пересчет в ней тривиален, так как мы точно знаем, куда перемещаются изменяемые поддеревья.