Алгоритм построения базы в пересечении матроидов — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 25 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | {{Задача | |
| − | Даны матроиды <tex>M_1 = | + | |definition= |
| + | Даны матроиды <tex>M_1 = \langle S, \mathcal{I}_1 \rangle</tex> и <tex>M_2 = \langle S, \mathcal{I}_2 \rangle</tex>. Необходимо найти максимальное по мощности независимое множество в [[Пересечение_матроидов,_определение,_примеры|пересечении]] <tex>M_1</tex> и <tex>M_2</tex>. | ||
| + | }} | ||
==Алгоритм решения== | ==Алгоритм решения== | ||
| − | Пусть множество <tex>J \in ( | + | Пусть множество <tex>J \in (\mathcal{I}_1 \cap \mathcal{I}_2)</tex>. |
| − | <br>Определим [[Граф замен для двух матроидов|граф замен]] <tex>D_{M_1, M_2}(J) = | + | <br>Определим [[Граф замен для двух матроидов|граф замен]] <tex>D_{M_1, M_2}(J) = \langle S, A(J) \rangle</tex>, где |
| − | <tex>A(J) = \{(y, z) | + | <tex>A(J) = \{(y, z) \mid y \in J, z \in S\setminus J, J - y + z \in \mathcal{I}_1 \} </tex> |
| − | <tex>\cup \{ (z', y') | + | <tex>\cup \{ (z', y') \mid z' \in S \setminus J, y' \in J, J - y' + z' \in \mathcal{I}_2 \}</tex>. |
| − | Пусть <tex>X_1 = \{ z \in S \setminus J | + | |
| + | Пусть <tex>X_1 = \{ z \in S \setminus J \mid J + z \in \mathcal{I}_1 \}</tex>, <tex>X_2 = \{ z \in S \setminus J \mid J + z \in \mathcal{I}_2 \}</tex>, <tex>P</tex> {{---}} кратчайший путь из <tex>X_1</tex> в <tex>X_2</tex> в графе <tex>D_{M_1, M_2}(J)</tex>. <tex>P</tex> может и не существовать. | ||
{{Лемма | {{Лемма | ||
|statement = | |statement = | ||
| − | Если в графе <tex>D_{M_1, M_2}(J)</tex> нет пути из <tex>X_1</tex> в <tex>X_2</tex>, то <tex>J</tex> - искомое максимальное по мощности независимое множество в пересечении <tex>M_1</tex> и <tex>M_2</tex> | + | Если в графе <tex>D_{M_1, M_2}(J)</tex> нет пути из <tex>X_1</tex> в <tex>X_2</tex>, то <tex>J</tex> {{---}} искомое максимальное по мощности независимое множество в пересечении <tex>M_1</tex> и <tex>M_2</tex>. |
|proof = | |proof = | ||
| − | Отметим, что если <tex>X_1</tex> или <tex>X_2</tex> пустые, то <tex>J</tex> - база в одном из исходных матроидов <tex>M_1</tex> или <tex>M_2</tex> и, следовательно, искомое максимальное по мощности независимое множество в пересечении <tex>M_1</tex> и <tex>M_2</tex>. Таким образом, предположим, что <tex>X_1</tex> и <tex>X_2</tex> непусты. Пусть <tex>U</tex> - множество вершин, из которых достижимы вершины из <tex>X_2</tex>. Отсутствие пути из <tex>X_1</tex> в <tex>X_2</tex> означает, что <tex>X_1 \cap U = \emptyset</tex>, <tex>X_2 \subseteq U</tex> и <tex>\delta^- (U) = \emptyset</tex> (т.е. в <tex>U</tex> не входит ни одной дуги). Тогда: | + | Отметим, что если <tex>X_1</tex> или <tex>X_2</tex> пустые, то <tex>J</tex> {{---}} база в одном из исходных матроидов <tex>M_1</tex> или <tex>M_2</tex> и, следовательно, искомое максимальное по мощности независимое множество в пересечении <tex>M_1</tex> и <tex>M_2</tex>. Таким образом, предположим, что <tex>X_1</tex> и <tex>X_2</tex> непусты. Пусть <tex>U</tex> {{---}} множество вершин, из которых достижимы вершины из <tex>X_2</tex>. Отсутствие пути из <tex>X_1</tex> в <tex>X_2</tex> означает, что <tex>X_1 \cap U = \emptyset</tex>, <tex>X_2 \subseteq U</tex> и <tex>\delta^- (U) = \emptyset</tex> (т.е. в <tex>U</tex> не входит ни одной дуги). Тогда: |
{{Утверждение | {{Утверждение | ||
|statement = | |statement = | ||
| − | <tex>r_1 (U) \ | + | <tex>r_1 (U) \leqslant |J \cap U|</tex> |
|proof = | |proof = | ||
| − | От противного. Пусть <tex>r_1 (U) > |J \cap U|</tex>, тогда <tex>\exists z \in U \setminus (J \cap U) | + | От противного. Пусть <tex>r_1 (U) > |J \cap U|</tex>, тогда <tex>\exists z \in U \setminus (J \cap U) : (J \cap U) + z \in \mathcal{I}_1</tex> при том, что <tex>J + z \notin \mathcal{I}_1</tex>. В противном случае <tex>J + z \in \mathcal{I}_1, z \in X_1</tex>, то есть <tex>X_1 \cap U \ne \emptyset</tex>, что противоречит отсутствию пути из <tex>X_1</tex> в <tex>X_2</tex>. Так как <tex>(J \cap U) + z \in \mathcal{I}_1</tex>, а <tex>J + z \notin \mathcal{I}_1</tex>, |
| − | + | <tex>\exists y \in J \setminus U : J - y + z \in \mathcal{I}_1</tex>. Однако, тогда <tex>(y, z) \in A(J)</tex>, что противоречит факту <tex>\delta^- (U) = \emptyset</tex>. | |
| − | <tex>\exists y \in J \setminus U | ||
}} | }} | ||
{{Утверждение | {{Утверждение | ||
|statement = | |statement = | ||
| − | <tex>r_2 (S \setminus U) \ | + | <tex>r_2 (S \setminus U) \leqslant |J \cap (S \setminus U)|</tex> |
|proof = | |proof = | ||
| − | От противного. Пусть <tex>\exists z \in (S \setminus U) \setminus J | + | От противного. Пусть <tex>\exists z \in (S \setminus U) \setminus J : J \cap (S \setminus U) + z \in \mathcal{I}_2</tex>. Аналогично доказательству предыдущего утверждения <tex>\exists y \in J \setminus (S \setminus U) : J - y + z \in \mathcal{I}_2</tex>. Однако <tex>J \setminus (S \setminus U) = J \cap U</tex>, то есть <tex>(z, y)</tex> {{---}} дуга в <tex>D_{M_1, M_2}(J)</tex>, поэтому <tex>z \in U</tex> (т.к. <tex>y \in U</tex>). Противоречие. |
}} | }} | ||
| − | Так как <tex>|J| = |J \cap U| + |J \setminus U| \ | + | Так как <tex>|J| = |J \cap U| + |J \setminus U| \geqslant r_1 (U) + r_2 (S \setminus U), |J| = r_1 (U) + r_2 (S \setminus U)</tex>. Следовательно, <tex>J</tex> {{---}} максимальное по мощности независимое множество в пересечении <tex>M_1</tex> и <tex>M_2</tex>. |
}} | }} | ||
{{Лемма | {{Лемма | ||
|statement = | |statement = | ||
| − | <tex>J' = J \bigtriangleup V(P) \in | + | <tex>J' = J \bigtriangleup V(P) \in \mathcal{I}_1 \cap \mathcal{I}_2</tex> |
|proof = | |proof = | ||
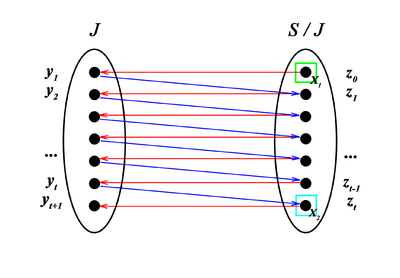
| − | [[ | + | [[Файл:Graph_DY.png|400px|thumb|right|Граф замен]] |
| − | Пусть <tex>P = z_0, y_1, z_1, ..., y_t, z_t | + | Пусть <tex>P = z_0, y_1, z_1, ..., y_t, z_t; G = \{ z_1, ..., z_t \} \cup (J \setminus \{ y_1, ..., y_t \})</tex>. Тогда <tex>G \subseteq S, |G| = |J|</tex> и дуги из <tex>\{ y_1, ..., y_t \}</tex> в |
| − | <tex>\{ z_1, ..., z_t \}</tex> составляют единственное полное паросочетание в <tex>J \bigtriangleup G</tex>. То есть, согласно [[Лемма о единственном паросочетании в графе замен | лемме о единственном паросочетании в подграфе замен]], <tex>G \in | + | <tex>\{ z_1, ..., z_t \}</tex> составляют единственное полное паросочетание в <tex>J \bigtriangleup G</tex>. То есть, согласно [[Лемма о единственном паросочетании в графе замен | лемме о единственном паросочетании в подграфе замен]], <tex>G \in \mathcal{I}_1</tex>. |
| − | К тому же, <tex>\forall i \ | + | К тому же, <tex>\forall i \geqslant 1\ z_i \notin X_1</tex>, иначе <tex>P</tex> {{---}} не кратчайший путь из <tex>X_1</tex> в <tex>X_2</tex>. Это означает, что <tex>z_i + J \notin \mathcal{I}_1</tex>, то есть |
| − | <tex>r_1 (J \cup G) = r_1 (J) = r_1 (G) = |G| = |J|</tex>. Так как <tex>J + z_0 \in | + | <tex>r_1 (J \cup G) = r_1 (J) = r_1 (G) = |G| = |J|</tex>. Так как <tex>J + z_0 \in \mathcal{I}_1, G + z_0 \in \mathcal{I}_1</tex> (т.е. <tex>J' = \{ z_0, z_1, ..., z_t \} \cup (J \setminus \{ y_1, ..., y_t \}) \in \mathcal{I}_1</tex>. |
| − | Симметрично | + | Симметрично <tex>G = \{ z_0, ..., z_{t - 1} \} \cup (J \setminus \{ y_1, ..., y_t \}), J' \in \mathcal{I}_2</tex> и, следовательно, <tex>J' \in (\mathcal{I}_1 \cap \mathcal{I}_2)</tex>. |
}} | }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | === Псевдокод === |
| − | ''Chandra Chekuri'' — [http://www.cs.illinois.edu/class/sp10/cs598csc/Lectures/Lecture17.pdf '''Combinatorial Optimization'''] | + | <tex>J</tex> = <tex>\emptyset</tex> |
| + | isMaximal = ''false'' | ||
| + | '''while''' '''not''' isMaximal | ||
| + | построить [[Граф замен для двух матроидов|граф замен]] <tex>D_{M_1, M_2}(J)</tex> | ||
| + | <tex>X_1 \leftarrow \{ z \in S \setminus J \mid J + z \in \mathcal{I}_1 \}</tex> | ||
| + | <tex>X_2 \leftarrow \{ z \in S \setminus J \mid J + z \in \mathcal{I}_2 \}</tex> | ||
| + | <tex>P</tex> <tex>\leftarrow</tex> кратчайший путь из <tex>X_1</tex> в <tex>X_2</tex> | ||
| + | '''if''' <tex>P \ne \emptyset</tex> | ||
| + | <tex>J</tex> = <tex>J \bigtriangleup V(P)</tex> | ||
| + | '''else''' | ||
| + | isMaximal = ''true'' | ||
| + | |||
| + | ==== Подсказки ==== | ||
| + | * Воспользуйтесь одним массивом для проверки множества на независимость по цветам, | ||
| + | * для проверки ацикличности графа при добавлении ребра можно использовать [[СНМ_(наивные_реализации)|СНМ]] или [[Обход_в_глубину,_цвета_вершин|обходом в глубину]], | ||
| + | * для нахождения кратчайшего пути можно использовать [[Обход_в_ширину|обход в ширину]], первоначально добавив фиктивную вершину, соединив её с вершинами из множества <tex>X_1</tex>. | ||
| + | |||
| + | == Теорема Эдмондса-Лоулера == | ||
| + | |||
| + | {{Теорема | ||
| + | |about= | ||
| + | Эдмондса-Лоулера | ||
| + | |statement= Пусть <tex>M_1=\langle X, \mathcal{I}_1\rangle</tex>, <tex>M_2=\langle X, \mathcal{I}_2\rangle</tex> {{---}} матроиды. Тогда <br> | ||
| + | <tex>\max\limits_{I \in \mathcal{I}_1 \cap \mathcal{I}_2 } |I| = \min\limits_{A \subseteq X} \left(r_1(A) + r_2(X \setminus A)\right)</tex>. | ||
| + | Где <tex>r_1</tex> и <tex>r_2</tex> {{---}} ранговые функции в первом и втором матроиде соответственно. | ||
| + | |proof= | ||
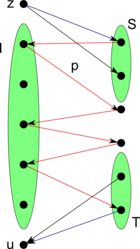
| + | [[Файл:El_graph2.png|thumb|140px|right|Граф замен, кратчайший путь]] | ||
| + | [[Файл:El_graph.png|thumb|140px|right|Завершение алгоритма]] | ||
| + | <div> | ||
| + | Докажем неравенство <tex>\max\limits_{I \in \mathcal{I}_1 \cap \mathcal{I}_2 } |I| \leqslant \min\limits_{A \subseteq X} \left(r_1(A) + r_2(X \setminus A)\right)</tex> | ||
| + | |||
| + | Выберем произвольные <tex>I \in \mathcal{I}_1 \cap \mathcal{I}_2</tex>, <tex>A \subseteq X</tex>, тогда | ||
| + | |||
| + | <tex>|I| = |I \cap A| + |I \cap (X \setminus A)|</tex> | ||
| + | |||
| + | <tex>I \cap A</tex> и <tex>I \cap (X \setminus A)</tex> {{---}} независимые в обоих матроидах (как подмножества независимового <tex>I</tex>), значит | ||
| + | |||
| + | <tex>|I| = r_1(I \cap A) + r_2(I \cap (X \setminus A))</tex> | ||
| + | |||
| + | Но <tex>r_1(I \cap A) \leqslant r_1(A)</tex> и <tex>r_2(I \cap (X \setminus A)) \leqslant r_2(X \setminus A)</tex>, значит | ||
| + | |||
| + | <tex>|I| \leqslant r_1(A) + r_2(X \setminus A)</tex> | ||
| + | |||
| + | В силу произвольности <tex>I</tex> и <tex>A</tex> получаем | ||
| + | |||
| + | <tex>\max\limits_{I \in \mathcal{I}_1 \cap \mathcal{I}_2 } |I| \leqslant \min\limits_{A \subseteq X} \left(r_1(A) + r_2(X \setminus A)\right)</tex> | ||
| + | |||
| + | |||
| + | Конструктивно построим <tex>\forall M_1, M_2</tex> такие <tex>I \in \mathcal{I}_1 \cap \mathcal{I}_2</tex> и <tex>A \subseteq X</tex>, что <tex>|I| = r_1(A) + r_2(X \setminus A)</tex>. | ||
| + | |||
| + | Обозначим <tex>S = \left\{x \mid I \cup \{x\} \in \mathcal{I}_1\right\}</tex>, <tex>T = \left\{x \mid I \cup \{x\} \in \mathcal{I}_2\right\}</tex>. Если <tex>S \cap T \ne \varnothing</tex>, добавим их пересечение в <tex>I</tex>. | ||
| + | |||
| + | Построим [[Граф замен для двух матроидов|граф замен]] <tex>G_I</tex>. Добавим вершину <tex>z</tex>, не влияющую на независимость в первом матроиде {{---}} из неё будут вести рёбра во все вершины множества <tex>S</tex>. Пусть <tex>p</tex> {{---}} кратчайший путь из <tex>S</tex> в <tex>T</tex>, <tex>p_1</tex> {{---}} путь <tex>p</tex> с добавленным в начало ребром из <tex>z</tex>. По [[Лемма о единственном паросочетании в графе замен|лемме о единственном паросочетании]] и [[Лемма о единственном паросочетании в подграфе замен, индуцированном кратчайшим путем|лемме о единственном паросочетании, индуцированном кратчайшем путём]] <tex>I \bigtriangleup p_1 \in \mathcal{I}_2</tex>. Теперь добавим вершину <tex>u</tex>, не влияющую на независимость во втором матроиде {{---}} в неё будут вести рёбра из всех вершин множества <tex>T</tex>. Тогда <tex>p_2</tex> (путь <tex>p</tex> с добавленным ребром в <tex>u</tex>) — кратчайший путь из <tex>S</tex> в <tex>u</tex>. Аналогично, <tex>I \bigtriangleup p_2 \in \mathcal{I}_1</tex>. Отсюда следует, что <tex>I \bigtriangleup p \in \mathcal{I}_1 \cap \mathcal{I}_2</tex>, причём <tex>|I \bigtriangleup p| = |I| + 1</tex>.</div> | ||
| + | |||
| + | Будем таким образом увеличивать <tex>I</tex>, пока существует путь <tex>p</tex>. Рассмотрим момент, когда такого пути не нашлось. | ||
| + | Введём обозначение: <tex>A = \{u \mid u \rightsquigarrow T\}</tex>. | ||
| + | |||
| + | Докажем, что <tex>r_1(A) = |I \cap A|</tex> от противного. | ||
| + | Пусть <tex>r_1(A) > |I \cap A|</tex>, тогда существует <tex>w \in A \setminus (I \cap A)</tex>, такое, что <tex>(I \cap A) \cup \{w\} \in \mathcal{I}_1</tex>. Если <tex>I \cup \{w\} \in \mathcal{I}_1</tex>, то <tex>w \in S</tex> и из <tex>S</tex> есть путь в <tex>A</tex>. Значит, <tex>I \cup \{w\} \notin \mathcal{I}_1</tex>. Отсюда следует, что существует <tex>y \in I \setminus A</tex>, такое что <tex>I \setminus \{y\} \cup \{w\} \in \mathcal{I}_1</tex>. Но тогда ребро <tex>yw</tex> имеется в графе, то есть из <tex>y</tex> существует путь в <tex>T</tex>, что противоречит условию <tex>y \in I \setminus A</tex>. | ||
| + | |||
| + | Следовательно, <tex>r_1(A) = |I \cap A|</tex>. Аналогично, <tex>r_2(\overline A) = |I \cap \overline A|</tex>. Отсюда <tex>r_1(A) + r_2(\overline A) = |I|</tex>, то есть при найденных <tex>I</tex> и <tex>A</tex> достигается равенство. | ||
| + | |||
| + | Построен пример равенства, значит, теорема доказана. | ||
| + | }} | ||
| + | |||
| + | == См. также== | ||
| + | * [[Пересечение матроидов, определение, примеры]] | ||
| + | * [[Алгоритм построения базы в объединении матроидов]] | ||
| + | |||
| + | == Источники информации == | ||
| + | * ''Chandra Chekuri'' — [http://www.cs.illinois.edu/class/sp10/cs598csc/Lectures/Lecture17.pdf '''Combinatorial Optimization'''] | ||
| + | |||
| + | [[Категория:Алгоритмы и структуры данных]] | ||
| + | [[Категория:Матроиды]] | ||
Текущая версия на 19:30, 4 сентября 2022
| Задача: |
| Даны матроиды и . Необходимо найти максимальное по мощности независимое множество в пересечении и . |
Содержание
Алгоритм решения
Пусть множество .
Определим граф замен , где
.
Пусть , , — кратчайший путь из в в графе . может и не существовать.
| Лемма: | ||||||||||
Если в графе нет пути из в , то — искомое максимальное по мощности независимое множество в пересечении и . | ||||||||||
| Доказательство: | ||||||||||
|
Отметим, что если или пустые, то — база в одном из исходных матроидов или и, следовательно, искомое максимальное по мощности независимое множество в пересечении и . Таким образом, предположим, что и непусты. Пусть — множество вершин, из которых достижимы вершины из . Отсутствие пути из в означает, что , и (т.е. в не входит ни одной дуги). Тогда:
| ||||||||||
| Лемма: |
| Доказательство: |
|
Пусть . Тогда и дуги из в составляют единственное полное паросочетание в . То есть, согласно лемме о единственном паросочетании в подграфе замен, . К тому же, , иначе — не кратчайший путь из в . Это означает, что , то есть . Так как (т.е. . Симметрично и, следовательно, . |
Псевдокод
= isMaximal = false while not isMaximal построить граф замен кратчайший путь из в if = else isMaximal = true
Подсказки
- Воспользуйтесь одним массивом для проверки множества на независимость по цветам,
- для проверки ацикличности графа при добавлении ребра можно использовать СНМ или обходом в глубину,
- для нахождения кратчайшего пути можно использовать обход в ширину, первоначально добавив фиктивную вершину, соединив её с вершинами из множества .
Теорема Эдмондса-Лоулера
| Теорема (Эдмондса-Лоулера): |
Пусть , — матроиды. Тогда . Где и — ранговые функции в первом и втором матроиде соответственно. |
| Доказательство: |
|
Докажем неравенство Выберем произвольные , , тогда
и — независимые в обоих матроидах (как подмножества независимового ), значит
Но и , значит
В силу произвольности и получаем
Обозначим , . Если , добавим их пересечение в . Построим граф замен . Добавим вершину , не влияющую на независимость в первом матроиде — из неё будут вести рёбра во все вершины множества . Пусть — кратчайший путь из в , — путь с добавленным в начало ребром из . По лемме о единственном паросочетании и лемме о единственном паросочетании, индуцированном кратчайшем путём . Теперь добавим вершину , не влияющую на независимость во втором матроиде — в неё будут вести рёбра из всех вершин множества . Тогда (путь с добавленным ребром в ) — кратчайший путь из в . Аналогично, . Отсюда следует, что , причём .Будем таким образом увеличивать , пока существует путь . Рассмотрим момент, когда такого пути не нашлось. Введём обозначение: . Докажем, что от противного. Пусть , тогда существует , такое, что . Если , то и из есть путь в . Значит, . Отсюда следует, что существует , такое что . Но тогда ребро имеется в графе, то есть из существует путь в , что противоречит условию . Следовательно, . Аналогично, . Отсюда , то есть при найденных и достигается равенство. Построен пример равенства, значит, теорема доказана. |
См. также
Источники информации
- Chandra Chekuri — Combinatorial Optimization