Квантовые алгоритмы — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 6 промежуточных версий 2 участников) | |||
| Строка 109: | Строка 109: | ||
}} | }} | ||
| − | '''Перефразируем задачу:''' у нас есть | + | '''Перефразируем задачу:''' у нас есть периодическая функция, для которой необходимо найти период путём нахождения [[Хеш-таблица|коллизии]]. Можно заметить, что алгоритм нахождения периода похож на алгоритм Саймона и фактически является его обобщением. |
[[Файл:Quantumalgorithm.QFT.png|470px|thumb|right|]] | [[Файл:Quantumalgorithm.QFT.png|470px|thumb|right|]] | ||
=== Реализация === | === Реализация === | ||
| − | + | Чтобы решить задачу, воспользуемся квантовым преобразованием Фурье<ref>[https://en.wikipedia.org/wiki/Quantum_Fourier_transform Wikipedia {{---}} Quantum Fourier transform]</ref>(далее <tex>QFT</tex>). <tex>QFT</tex> {{---}} гейт, который реализует матрицу дискретного преобразования Фурье<ref>[https://ru.wikipedia.org/wiki/%D0%94%D0%B8%D1%81%D0%BA%D1%80%D0%B5%D1%82%D0%BD%D0%BE%D0%B5_%D0%BF%D1%80%D0%B5%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D0%A4%D1%83%D1%80%D1%8C%D0%B5 Википедия {{---}} Дискретное преобразование Фурье]</ref> над квантовым состоянием. Для начала инициализируем начальные кубиты состоянием ноль. Проводим их всех через гейт <tex>QFT</tex> и получаем все возможные равновероятные суперпозиции всех булевых состояний <math>N</math> такие, что: | |
| − | Чтобы решить задачу, воспользуемся квантовым преобразованием Фурье<ref>[https://en.wikipedia.org/wiki/Quantum_Fourier_transform Wikipedia {{---}} Quantum Fourier transform]</ref>( | ||
| − | <tex> QFT_N | + | <tex>|0 \rangle |0 \rangle \xrightarrow{QFT_N} \dfrac{1}{\sqrt{N}} \sum\limits_{x=0}^{N-1} |x \rangle |0 \rangle</tex> |
| − | |||
| − | |||
| − | \\ | ||
| − | |||
| − | |||
| − | + | Суперпозиции передаём в гейт <tex>U_f</tex>, который реализует унитарное преобразование<ref>[https://ru.wikipedia.org/wiki/%D0%A3%D0%BD%D0%B8%D1%82%D0%B0%D1%80%D0%BD%D1%8B%D0%B9_%D0%BE%D0%BF%D0%B5%D1%80%D0%B0%D1%82%D0%BE%D1%80 Википедия {{---}} Унитарный оператор]</ref>, которое переводит <tex>|x \rangle |0 \rangle</tex> в <tex>|x \rangle |f(x) \rangle:</tex> | |
| + | |||
| + | <tex>\dfrac{1}{\sqrt{N}} \sum\limits_{x=0}^{N-1} |x \rangle |0 \rangle \xrightarrow{U_f} \dfrac{1}{\sqrt{N}} \sum\limits_{x=0}^{N-1} |x \rangle |f(x) \rangle</tex> | ||
| + | |||
| + | Чтобы получить из этого периодическую суперпозицию, мы измеряем <tex>|f\rangle</tex> и поскольку <tex>f</tex> периодическая, её прообраз это <tex>f(x_0)</tex>, такой что <tex>\{x_0,x_0+r,x_0+2r,\ldots,x_0+(\dfrac{N}{r}-1)r)\}</tex>: | ||
| + | |||
| + | <tex>\dfrac{1}{\sqrt{N}} \sum\limits_{x=0}^{N-1} |x \rangle |f(x) \rangle \xrightarrow{measure|f\rangle} \sqrt{\dfrac{r}{N}} \sum\limits_{i=0}^{N/r-1} |ir+x_0 \rangle |f(x_0) \rangle</tex> | ||
| + | |||
| + | Теперь наш первый регистр находится в периодической суперпозиции, где период такой же, как период функции, но мы не можем сразу его просто измерить, потому что мы можем измерить другое значение <tex>|f\rangle</tex>, ведь мы получили периодическую суперпозицию, которая случайно линейно смещена и мы не получим никакой полезной информации. | ||
| + | |||
| + | [[Файл:Quantum algorithm. QFT. Graph3.jpg|270px|thumb|right|]]Поэтому вместо этого мы применим <tex>QFT</tex> и будем полагаться на его свойства, чтобы получить информацию, которая нам нужна. Идея в следующем: есть периодическая функция с периодом <tex>r</tex>, после применения <tex>QFT</tex>, получим новую периодическую функцию с периодом <tex>N/r</tex>, где <tex>N</tex> {{---}} модуль, с которым мы работаем: | ||
| + | |||
| + | <tex>\sqrt{\dfrac{r}{N}} \sum\limits_{i=0}^{N/r-1} |ir+x_0 \rangle \xrightarrow{QFT_N} \dfrac{1}{\sqrt{r}} \sum\limits_{i=0}^{r-1} |i\dfrac{N}{r} \rangle φ_i</tex>, где <tex>φ_i</tex> {{---}} некоторый неважный период, возникающий из линейного сдвига <tex>x_0</tex>. | ||
| + | |||
| + | Так мы уже можем измерить и извлечь <tex>m\dfrac{N}{r}</tex>, для некоторого целого <tex>m</tex>. | ||
| + | |||
| + | Теперь мы повторяем алгоритм, чтобы получить несколько различных кратных <tex>\dfrac{N}{r}</tex>. Как только у нас будет достаточно значений, мы можем вычислить их наибольший общий делитель<ref>[https://ru.wikipedia.org/wiki/%D0%9D%D0%B0%D0%B8%D0%B1%D0%BE%D0%BB%D1%8C%D1%88%D0%B8%D0%B9_%D0%BE%D0%B1%D1%89%D0%B8%D0%B9_%D0%B4%D0%B5%D0%BB%D0%B8%D1%82%D0%B5%D0%BB%D1%8C Википедия {{---}} Наибольший общий делитель]</ref>, который, с некоторой вероятностью, будет искомым периодом <tex>r</tex>, при этом вероятность ошибки будет экспоненциально падать с каждой попыткой. | ||
''Примечание:'' Алгоритм нахождения периода используется в алгоритме Шора<ref>[https://en.wikipedia.org/wiki/Shor%27s_algorithm Wikipedia {{---}} Shor's algorithm]</ref>, который позволяет решать задачу [[Разложение на множители (факторизация)|факторизации числа]]. | ''Примечание:'' Алгоритм нахождения периода используется в алгоритме Шора<ref>[https://en.wikipedia.org/wiki/Shor%27s_algorithm Wikipedia {{---}} Shor's algorithm]</ref>, который позволяет решать задачу [[Разложение на множители (факторизация)|факторизации числа]]. | ||
| Строка 130: | Строка 140: | ||
'''''Квантовый алгоритм:''''' <tex>O(\log N)</tex>. | '''''Квантовый алгоритм:''''' <tex>O(\log N)</tex>. | ||
| + | |||
== См.также == | == См.также == | ||
* [[Квантовые гейты]] | * [[Квантовые гейты]] | ||
| Строка 151: | Строка 162: | ||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
| + | |||
| + | [[Категория: Схемы из функциональных элементов]] | ||
Текущая версия на 19:32, 4 сентября 2022
| Определение: |
| Квантовый алгоритм (англ. quantum algorithm) представляет собой классический алгоритм, который задает последовательность унитарных операций (гейтов, или вентилей) с указанием, над какими именно кубитами[1] их надо совершать. |
Содержание
Алгоритм проверки чётности
Постановка задачи
| Задача: |
| Пусть имеется функция , такая, что с неизвестным . Найти за минимальное количество обращений к функции . |
Пример:
Если
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
то .
Реализация
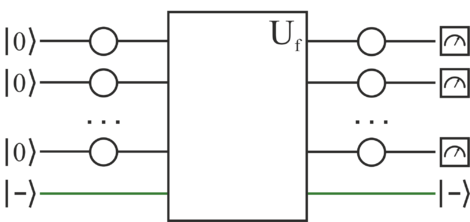
Для начала инициализируем начальные кубитов состоянием ноль. Проводим их всех через гейт Адамара (англ. Hadamard gate)[2] и получаем все возможные суперпозиции. Суперпозиции передаём в "черный ящик", который реализован в виде вентиля . Сам результат опять пропускаем через гейт Адамара. В конце измеряем результат, который будет являться искомой .
В качестве бита, который будет содержать ответ, будет использоваться суперпозиция:
Выразим неизвестную:
Сложность
Классический алгоритм: .
Квантовый алгоритм: . Такая сложность достигается благодаря квантовым свойствам[3], а конкретно параллелизму[4].
Алгоритм Саймона
Постановка задачи
| Задача: |
| Пусть имеется функция , такая, что с неизвестным . Найти за минимальное количество обращений к функции . |
Пример:
Если
| 101 | 010 | 000 | 110 | 000 | 110 | 101 | 010 |
то .
Реализация
Задача похожа на задачу нахождения коллизии, так как необходимо найти два значения, при которых их выходные значения будет одинаковыми, затем вычислить между ними разницу, которая и будет ответом задачи.
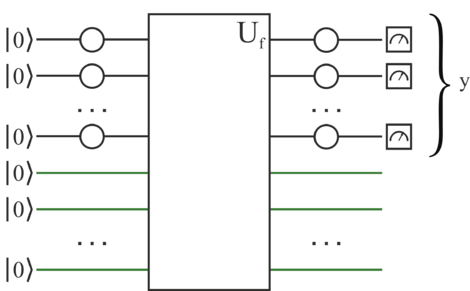
Аналогично предыдущему алгоритму все возможные суперпозиции передаём в "черный ящик", полученный результат опять пропускаем через гейт Адамара. В конце измеряем полученные значения, которые будут являться некоторой строкой , дающей ноль при скалярном умножении на искомую . После итерации алгоритма получим систему из линейных уравнений; решив эту систему уравнений, найдём искомую :
где , и , при и .
Особенности алгоритма:
- для решения СЛАУ [5] необходим препроцессинг на классическом компьютере;
- алгоритм может допускать ошибку(возможно, какие-то уравнения не будут линейно независимыми и система не будет иметь решений) с вероятностью при одном цикле прохода алгоритма. Этого можно избежать, если прогнать алгоритм несколько раз, так для раз, вероятность будет равна: . Например, при вероятность будет .
Сложность
Классический алгоритм: .
Квантовый алгоритм: .
Алгоритм нахождения периода
Постановка задачи
| Задача: |
| Пусть имеется функция , такая, что с неизвестным периодом . Найти за минимальное количество обращений к функции . |
Перефразируем задачу: у нас есть периодическая функция, для которой необходимо найти период путём нахождения коллизии. Можно заметить, что алгоритм нахождения периода похож на алгоритм Саймона и фактически является его обобщением.
Реализация
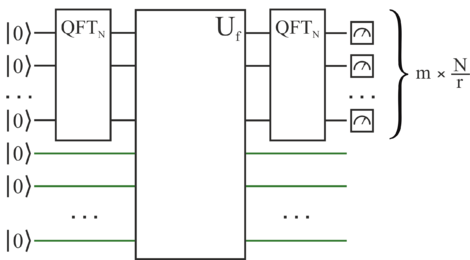
Чтобы решить задачу, воспользуемся квантовым преобразованием Фурье[6](далее ). — гейт, который реализует матрицу дискретного преобразования Фурье[7] над квантовым состоянием. Для начала инициализируем начальные кубиты состоянием ноль. Проводим их всех через гейт и получаем все возможные равновероятные суперпозиции всех булевых состояний такие, что:
Суперпозиции передаём в гейт , который реализует унитарное преобразование[8], которое переводит в
Чтобы получить из этого периодическую суперпозицию, мы измеряем и поскольку периодическая, её прообраз это , такой что :
Теперь наш первый регистр находится в периодической суперпозиции, где период такой же, как период функции, но мы не можем сразу его просто измерить, потому что мы можем измерить другое значение , ведь мы получили периодическую суперпозицию, которая случайно линейно смещена и мы не получим никакой полезной информации.
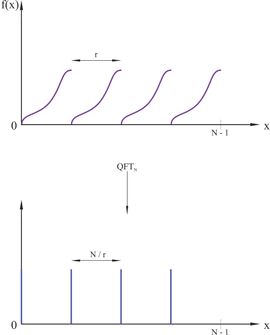
Поэтому вместо этого мы применим и будем полагаться на его свойства, чтобы получить информацию, которая нам нужна. Идея в следующем: есть периодическая функция с периодом , после применения , получим новую периодическую функцию с периодом , где — модуль, с которым мы работаем:, где — некоторый неважный период, возникающий из линейного сдвига .
Так мы уже можем измерить и извлечь , для некоторого целого .
Теперь мы повторяем алгоритм, чтобы получить несколько различных кратных . Как только у нас будет достаточно значений, мы можем вычислить их наибольший общий делитель[9], который, с некоторой вероятностью, будет искомым периодом , при этом вероятность ошибки будет экспоненциально падать с каждой попыткой.
Примечание: Алгоритм нахождения периода используется в алгоритме Шора[10], который позволяет решать задачу факторизации числа.
Сложность
Классический алгоритм: .
Квантовый алгоритм: .
См.также
Примечания
- ↑ Википедия — Кубит
- ↑ Wikipedia — Hadamard gate
- ↑ Википедия — Квантовый компьютер
- ↑ Википедия — Квантовый параллелизм
- ↑ Википедия — Система линейных алгебраических уравнений
- ↑ Wikipedia — Quantum Fourier transform
- ↑ Википедия — Дискретное преобразование Фурье
- ↑ Википедия — Унитарный оператор
- ↑ Википедия — Наибольший общий делитель
- ↑ Wikipedia — Shor's algorithm
Источники информации
- Implementation of a quantum algorithm to solve Bernstein-Vazirani’s parity problem without entanglement on an ensemble quantum computer
- Wikipedia — Simon's problem
- Гайнутдинова А. Ф. "Квантовые вычисления"
- Соловьев В. М. "Квантовые компьютеры и квантовые алгоритмы. Часть 1. Квантовые компьютеры"
- Соловьев В. М. "Квантовые компьютеры и квантовые алгоритмы. Часть 2. Квантовые алгоритмы"
- Wikipedia — Quantum Fourier transform
- Quantum parity algorithms as oracle calls, and application in Grover Database search
- Wikipedia — Shor's algorithm
- Веб-приложение, использующее WebGL, чтобы имитировать до 22 кубитов на GPU
- Веб-приложение, для написания и визуализации квантовых алгоритмов
- Языки программирования для квантового компьютера