Cортировка слиянием с использованием O(1) дополнительной памяти — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 46 промежуточных версий 12 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | {{boring}} | |
| + | В конспекте содержится несколько ошибок, которые никто не исправлял уже лет 5, половины доказательств нету и вообще это стоит переписать. Если хотите заимплементить корректный алгоритм, придется дополнительно подумать головой. Алсо, про "сравнение в реальных условиях" - бред, по времени этот алгоритм в несколько раз медленнее std::sort. ~[[Участник:Yurik|Yurik]]~, 2017 | ||
| − | + | <br/> | |
| − | |||
| − | |||
| − | |||
| − | + | На вход алгоритм получает массив, который состоит из двух отсортированных частей. Нам необходимо за <tex>O(1)</tex> дополнительной памяти и <tex>O(n)</tex> времени получить отсортированный массив.<br> | |
| + | В реализации алгоритм весьма громоздкий. Но сравнение в реальных условиях реализации на C++ (на массивах длиной до <tex>10^8</tex>) показало, что по числу сравнений алгоритм выигрывает у qsort примерно 10%, а по общему времени работы – от <tex>1.2</tex> до <tex>1.3</tex> раз. | ||
| − | == | + | == Алгоритм == |
| − | + | У нас есть массив, который состоит из двух отсортированных частей: | |
| − | |||
| − | + | [[Файл:Merge_O(1)_1.png|525px]] | |
| − | = | + | Разобьем наш массив на <tex>cnt</tex> подряд идущих блоков длиной <tex>len = \lfloor \sqrt{n} \rfloor </tex>. Остаток трогать не будем. |
| − | |||
| − | + | [[Файл:Merge_O(1)_2.png|525px]] | |
| − | |||
| − | + | Найдем блок, содержащий конец первой отсортированной части. Поменяем его с последним блоком. В дальнейшем будем использовать его как буфер обмена. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Файл:Merge_O(1)_3.png|525px]] | |
| − | + | Отсортируем блоки по возрастанию по первому элементу (если первые элементы равны, тогда по последнему). | |
| − | + | [[Файл:Merge_O(1)_4.png|525px]] | |
| − | |||
| − | + | Для этого подойдет любая квадратичная или более быстрая сортировка, которая требует <tex> O (1) </tex> дополнительной памяти. Для сохранения линейной асимптотики надо использовать алгоритм, линейный по числу обменов, т.е. подходит [[Сортировка выбором|сортировка выбором]]. Так как блоков <tex> \sqrt{n} </tex>, то количество операций на этом шаге <tex> O(n) </tex>. | |
| − | + | Следует заметить, что, после сортировки этих блоков, элементы, которые стоят левее заданного и больше его, находились в противоположной части отсортированного массива, также они находятся в пределах одной группы, поэтому количество инверсий для каждого элемента не больше <tex>\sqrt{n}</tex>. | |
| − | |||
| − | 1. | + | Пользуясь буфером обмена, последовательно сольем пары соседних блоков <tex>([0, ~ len - 1]</tex> и <tex>[len, ~ 2 ~ len - 1],</tex> потом <tex>[len, ~ 2 ~ len - 1]</tex> и <tex>[2 ~ len, ~ 3 ~ len - 1],</tex> и т.д.<tex>)</tex>. |
| − | + | Попытаемся слить первый и второй блок. Поменяем местами первый блок с буфером обмена. И, как в обычном слиянии, пользуясь двумя указателями, сливаем второй блок и только что измененный буфер. Результат начинаем записывать с начала первого блока. Чтобы не потерять данные, вместо записи используем обмен элементов. Так как блоки имеют одинаковую длину и между указателем на второй блок и указателем на запись расстояние равно длине блока, то слияние произойдет корректно (пример использования буфера обмена приведен ниже). | |
| − | + | [[Файл:Merge_O(1)_5.png|525px]] | |
| − | Количество операций на этом | + | Так как после предыдущего шага количество инверсий для каждого элемента не больше <tex>\sqrt{n}</tex>, то ему надо сдвинуться влево не больше, чем на <tex>\sqrt{n}</tex> элементов, поэтому в результате мы получим, что первые <tex>len \cdot (cnt - 1)</tex> элементов исходного массива отсортированы. Количество блоков <tex> \sqrt{n} </tex> и каждое слияние работает за <tex> О O(\sqrt{n}) </tex> , поэтому количество операций на этом шаге <tex> O(n) </tex>. |
| − | + | ||
| − | = | + | <tex>S</tex> {{---}} размер остатка вместе с буфером. Используя квадратичную или более быструю сортировку, которая требует <tex> O(1) </tex> дополнительной памяти, отсортируем подмассив длиной <tex> 2S </tex>, который находится в конце. |
| − | *[http://e-maxx.ru/bookz/files/knuth_3.djvu | + | |
| − | *[http://pastebin.com/hN2SnEfP Реализация алгоритма на JAVA] | + | Так как <tex>S < 2 \sqrt{n}</tex>, то сортировка пройдет за <tex>O(n)</tex>. |
| + | |||
| + | [[Файл:Merge_O(1)_6.png|525px]] | ||
| + | |||
| + | Теперь на последних <tex> S </tex> местах будут находиться <tex> S </tex> максимальных элементов. Оставшаяся часть представляет собой массив, содержащий две отсортированные части, причем размер второй равен <tex> S </tex>. По аналогии с тем что делали раньше, только в обратную сторону, отсортируем оставшуюся часть, разделив ее на блоки длиной <tex>S</tex>, используя последние <tex>S</tex> как буфер обмена. Не забудем после отсортировать буфер обмена. | ||
| + | |||
| + | [[Файл:Merge_O(1)_7.png|525px]] | ||
| + | |||
| + | В результате мы получили отсортированный исходный массив. | ||
| + | |||
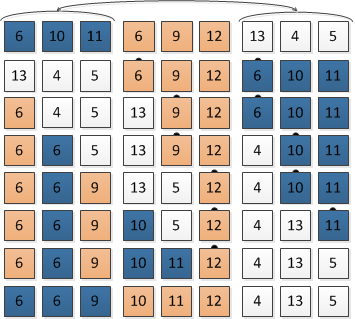
| + | == Пример использования буфера обмена == | ||
| + | |||
| + | [[Файл:Merge_O(1)_buffer.png|355px]] | ||
| + | |||
| + | == Источники информации == | ||
| + | *[http://habrahabr.ru/post/138146/ Habrahabr {{---}}Сортировка слиянием без использования дополнительной памяти ] | ||
| + | *[http://e-maxx.ru/bookz/files/knuth_3.djvu Д.Е.Кнут {{---}} Искусство программирования (том 3) упр 18 к разделу 5.2.4] | ||
| + | *[http://pastebin.com/hN2SnEfP PASTEBIN {{---}} Реализация алгоритма на JAVA] | ||
| + | |||
| + | [[Категория: Дискретная математика и алгоритмы]] | ||
| + | [[Категория: Сортировки]] | ||
Текущая версия на 19:33, 4 сентября 2022
| Эта статья сделана из уныния и отчаяния. Сделайте с ней что-нибудь. Пожалуйста. |
В конспекте содержится несколько ошибок, которые никто не исправлял уже лет 5, половины доказательств нету и вообще это стоит переписать. Если хотите заимплементить корректный алгоритм, придется дополнительно подумать головой. Алсо, про "сравнение в реальных условиях" - бред, по времени этот алгоритм в несколько раз медленнее std::sort. ~Yurik~, 2017
На вход алгоритм получает массив, который состоит из двух отсортированных частей. Нам необходимо за дополнительной памяти и времени получить отсортированный массив.
В реализации алгоритм весьма громоздкий. Но сравнение в реальных условиях реализации на C++ (на массивах длиной до ) показало, что по числу сравнений алгоритм выигрывает у qsort примерно 10%, а по общему времени работы – от до раз.
Алгоритм
У нас есть массив, который состоит из двух отсортированных частей:
Разобьем наш массив на подряд идущих блоков длиной . Остаток трогать не будем.
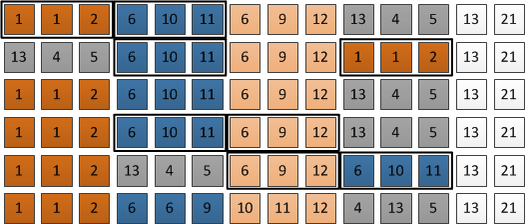
Найдем блок, содержащий конец первой отсортированной части. Поменяем его с последним блоком. В дальнейшем будем использовать его как буфер обмена.
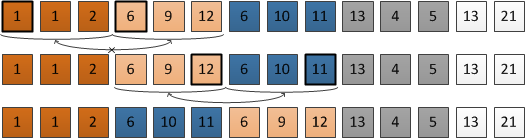
Отсортируем блоки по возрастанию по первому элементу (если первые элементы равны, тогда по последнему).
Для этого подойдет любая квадратичная или более быстрая сортировка, которая требует дополнительной памяти. Для сохранения линейной асимптотики надо использовать алгоритм, линейный по числу обменов, т.е. подходит сортировка выбором. Так как блоков , то количество операций на этом шаге .
Следует заметить, что, после сортировки этих блоков, элементы, которые стоят левее заданного и больше его, находились в противоположной части отсортированного массива, также они находятся в пределах одной группы, поэтому количество инверсий для каждого элемента не больше .
Пользуясь буфером обмена, последовательно сольем пары соседних блоков и потом и и т.д..
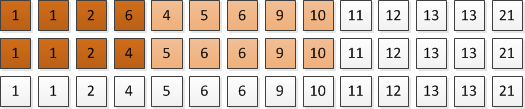
Попытаемся слить первый и второй блок. Поменяем местами первый блок с буфером обмена. И, как в обычном слиянии, пользуясь двумя указателями, сливаем второй блок и только что измененный буфер. Результат начинаем записывать с начала первого блока. Чтобы не потерять данные, вместо записи используем обмен элементов. Так как блоки имеют одинаковую длину и между указателем на второй блок и указателем на запись расстояние равно длине блока, то слияние произойдет корректно (пример использования буфера обмена приведен ниже).
Так как после предыдущего шага количество инверсий для каждого элемента не больше , то ему надо сдвинуться влево не больше, чем на элементов, поэтому в результате мы получим, что первые элементов исходного массива отсортированы. Количество блоков и каждое слияние работает за , поэтому количество операций на этом шаге .
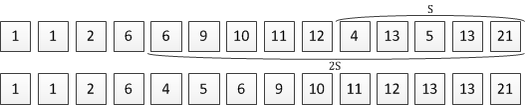
— размер остатка вместе с буфером. Используя квадратичную или более быструю сортировку, которая требует дополнительной памяти, отсортируем подмассив длиной , который находится в конце.
Так как , то сортировка пройдет за .
Теперь на последних местах будут находиться максимальных элементов. Оставшаяся часть представляет собой массив, содержащий две отсортированные части, причем размер второй равен . По аналогии с тем что делали раньше, только в обратную сторону, отсортируем оставшуюся часть, разделив ее на блоки длиной , используя последние как буфер обмена. Не забудем после отсортировать буфер обмена.
В результате мы получили отсортированный исходный массив.