Персистентный стек — различия между версиями
(→Реализация на массиве) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 14 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
== Алгоритм == | == Алгоритм == | ||
| − | + | ||
| − | |||
| − | |||
=== Реализация на массиве === | === Реализация на массиве === | ||
Заведем массив запросов, модифицирующих стек.<br> | Заведем массив запросов, модифицирующих стек.<br> | ||
| + | '''struct''' '''Query''': | ||
| + | '''T''' value | ||
| + | '''uint''' prev | ||
У каждого элемента массива будет <tex>2</tex> поля: значение в вершине стека и индекс предыдущей версии стека.<br> | У каждого элемента массива будет <tex>2</tex> поля: значение в вершине стека и индекс предыдущей версии стека.<br> | ||
Тогда операции push и pop будут иметь следующий вид:<br> | Тогда операции push и pop будут иметь следующий вид:<br> | ||
| Строка 12: | Строка 13: | ||
s[s.top].value = x | s[s.top].value = x | ||
s[s.top].prev = i | s[s.top].prev = i | ||
| − | * <tex>\mathrm{pop}(i)</tex> {{---}} возвращает значение, хранящееся в элементе с номером <tex>i</tex> и копирует элемент, предыдущий для него, | + | * <tex>\mathrm{pop}(i)</tex> {{---}} возвращает значение, хранящееся в элементе с номером <tex>i</tex> и копирует элемент, предыдущий для него, результирующий стек будет иметь номер <tex> n + 1 </tex>. |
| − | результирующий стек будет иметь номер <tex> n + 1 </tex>. | ||
'''T''' pop(i : '''uint'''): | '''T''' pop(i : '''uint'''): | ||
| − | ''' | + | '''Query''' k = s[i] |
k = s[k.prev] | k = s[k.prev] | ||
push(k.prev, k.value) | push(k.prev, k.value) | ||
| Строка 21: | Строка 21: | ||
=== Реализация на списке === | === Реализация на списке === | ||
| − | + | Будем использовать узел, у которого будет значение и ссылка на прошлую версию стека. При этом сам узел - это версия стека. | |
| − | + | '''struct''' '''Node''': | |
| + | '''T''' value | ||
| + | '''Node''' prev | ||
| + | Будем хранить состояния в узлах. Будем возвращать пользователю информацию о текущей вершине.<br> | ||
У каждого узла будет <tex>2</tex> поля: значение в вершине стека и ссылка на предыдущую версию стека.<br> | У каждого узла будет <tex>2</tex> поля: значение в вершине стека и ссылка на предыдущую версию стека.<br> | ||
| + | Сам персистентный стек будет обозначаться <tex>s</tex>.<br> | ||
* <tex> \mathrm{push}(i, x)</tex> {{---}} добавляет элемент <tex>x</tex> в стек узла <tex>i</tex>, | * <tex> \mathrm{push}(i, x)</tex> {{---}} добавляет элемент <tex>x</tex> в стек узла <tex>i</tex>, | ||
| Строка 34: | Строка 38: | ||
* <tex>\mathrm{pop}(i)</tex> {{---}} возвращает значение, хранящееся в узле <tex>i</tex> и копирует элемент, предыдущий для него. | * <tex>\mathrm{pop}(i)</tex> {{---}} возвращает значение, хранящееся в узле <tex>i</tex> и копирует элемент, предыдущий для него. | ||
'''pair<T, Stack>''' pop(i : '''Node'''): | '''pair<T, Stack>''' pop(i : '''Node'''): | ||
| − | ''' | + | '''T''' val = i.value |
| − | + | i = i.prev | |
| − | '''return''' pair( | + | '''return''' pair(val, s) |
== Пример == | == Пример == | ||
| Строка 94: | Строка 98: | ||
| − | Выполним <tex>\mathrm{pop}(3)</tex>. | + | Выполним <tex>\mathrm{pop}(3)</tex>. Он возвращает <tex>5</tex> и копирует 2-ую вершину. |
[[Файл:стек4.png|500px|nothumb|right|]] | [[Файл:стек4.png|500px|nothumb|right|]] | ||
{| border = 1; cellspacing = 0; class="wikitable" | {| border = 1; cellspacing = 0; class="wikitable" | ||
| Строка 159: | Строка 163: | ||
В итоге мы имеем доступ ко всем версиям стека за <tex>O(1)</tex> времени и <tex>O(n)</tex> памяти. | В итоге мы имеем доступ ко всем версиям стека за <tex>O(1)</tex> времени и <tex>O(n)</tex> памяти. | ||
| − | == | + | == Применение == |
| − | + | Используя персистентый стек, можно реализовать легко перстистентную очередь (если вспомнить её реализацию на двух стеках). <br> | |
| + | См. [[Персистентная очередь]] | ||
== См. также== | == См. также== | ||
Текущая версия на 19:33, 4 сентября 2022
Содержание
Алгоритм
Реализация на массиве
Заведем массив запросов, модифицирующих стек.
struct Query: T value uint prev
У каждого элемента массива будет поля: значение в вершине стека и индекс предыдущей версии стека.
Тогда операции push и pop будут иметь следующий вид:
- — добавляет элемент в стек с номером , результирующий стек будет иметь номер ,
function push(i : uint, x : T): s.top = s.top + 1 s[s.top].value = x s[s.top].prev = i
- — возвращает значение, хранящееся в элементе с номером и копирует элемент, предыдущий для него, результирующий стек будет иметь номер .
T pop(i : uint): Query k = s[i] k = s[k.prev] push(k.prev, k.value) return s[i].value
Реализация на списке
Будем использовать узел, у которого будет значение и ссылка на прошлую версию стека. При этом сам узел - это версия стека.
struct Node: T value Node prev
Будем хранить состояния в узлах. Будем возвращать пользователю информацию о текущей вершине.
У каждого узла будет поля: значение в вершине стека и ссылка на предыдущую версию стека.
Сам персистентный стек будет обозначаться .
- — добавляет элемент в стек узла ,
Stack push(i : Node, x : T): k.value = x k.prev = i s.top = k return s
- — возвращает значение, хранящееся в узле и копирует элемент, предыдущий для него.
pair<T, Stack> pop(i : Node): T val = i.value i = i.prev return pair(val, s)
Пример
Пусть изначально у нас есть один пустой стек. Запишем его в массив.
| index | 1 |
|---|---|
| value | |
| prev |
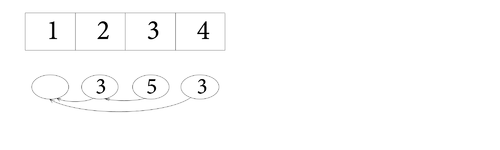
Далее выполним . Создается новая вершина со значением , ссылающаяся на 1-ую, помещаем ее во 2-ую ячейку массива:
| index | 1 | 2 |
|---|---|---|
| value | 3 | |
| prev | 1 |
Аналогично выполним :
| index | 1 | 2 | 3 |
|---|---|---|---|
| value | 3 | 5 | |
| prev | 1 | 2 |
Выполним . Он возвращает и копирует 2-ую вершину.
| index | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| value | 3 | 5 | 3 | |
| prev | 1 | 2 | 1 |
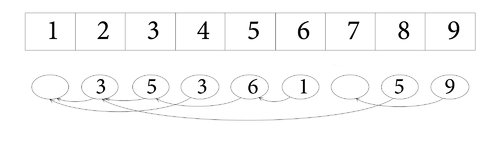
Так будет выглядеть массив после последовательности операций
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| value | 3 | 5 | 3 | 6 | 1 | 5 | 9 | ||
| prev | 1 | 2 | 1 | 3 | 5 | 2 | 7 |
В итоге мы имеем доступ ко всем версиям стека за времени и памяти.
Применение
Используя персистентый стек, можно реализовать легко перстистентную очередь (если вспомнить её реализацию на двух стеках).
См. Персистентная очередь