Алгоритм Касаи и др. — различия между версиями
(→Факт №2) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 24 промежуточные версии 8 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Алгоритм Касаи''' ( | + | '''Алгоритм Касаи, Аримуры, Арикавы, Ли, Парка''' (англ. ''Kasai, Arimura, Arikawa, Lee, Park algorithm'') {{---}} алгоритм, позволяющий за линейное время вычислить длину наибольших общих префиксов (англ. ''longest common prefix'', ''LCP'') для всех соседних суффиксов строки, отсортированных в лексикографическом порядке. |
| − | длину наибольших общих префиксов для соседних | ||
| − | порядке | ||
==Обозначения== | ==Обозначения== | ||
| − | + | Введём следующие обозначения: | |
| + | * <tex>S</tex> {{---}} данная строка. | ||
| + | * <tex>S_{i}</tex> {{---}} суффикс строки <tex>S</tex>, начинающийся в <tex>i</tex>-ом символе. | ||
| + | * <tex>Suf</tex> {{---}} [[Суффиксный массив | суффиксный массив]]. | ||
| + | * <tex>Suf^{-1}</tex> {{---}} массив, обратный суффиксному, который может быть получен немедленно, если задан массив <tex>Suf</tex>. Если <tex>Suf[k] = i</tex>, то <tex>Suf^{-1}[i] = k</tex>. | ||
| + | * <tex>LCP(S_{Suf[x]}, S_{Suf[z]})</tex> {{---}} длина наибольшего общего префикса строк <tex>S_{Suf[x]}</tex> и <tex>S_{Suf[z]}</tex>. | ||
| + | * <tex>lcp[i]</tex> {{---}} длина наибольшего общего префикса соседних строк <tex>i-1</tex> и <tex>i</tex>, то есть <tex>lcp[i] = LCP(S_{Suf[i-1]}, S_{Suf[i]})</tex>. | ||
| − | <tex> | + | ==Некоторые свойства LCP== |
| − | + | {{Утверждение | |
| − | + | |id = fact1 | |
| − | + | |about= №1 | |
| − | <tex>LCP</tex> между двумя суффиксами {{---}} | + | |statement= |
| + | <tex>LCP(S_{Suf[y - 1]}, S_{Suf[y]}) \geqslant LCP(S_{Suf[x]},S_{Suf[z]}), x < y \leqslant z</tex> | ||
| + | |proof= | ||
| + | <tex>LCP</tex> между двумя суффиксами {{---}} минимум <tex>LCP</tex> всех пар соседних суффиксов между ними в суффиксном массиве <tex>Suf</tex>. То есть <tex>LCP(S_{Suf[x]}, S_{Suf[z]}) = \min\limits_{x < y \leqslant z}LCP(S_{Suf[y - 1]},S_{Suf[y]})</tex>. | ||
Отсюда следует, что <tex>LCP</tex> пары соседних суффиксов в массиве <tex>Suf</tex> больше или равно <tex>LCP</tex> пары суффиксов, окружающих их. | Отсюда следует, что <tex>LCP</tex> пары соседних суффиксов в массиве <tex>Suf</tex> больше или равно <tex>LCP</tex> пары суффиксов, окружающих их. | ||
| − | |||
| − | |||
| − | |||
}} | }} | ||
| − | + | Также заметим, что <tex>LCP(S_{Suf[x]}, S_{Suf[z]}) = \min\limits_{i = x + 1 \ldots z}lcp[i]</tex>. | |
| − | |||
| − | |||
{{Утверждение | {{Утверждение | ||
| + | |id = fact2 | ||
| + | |about= №2 | ||
|statement= | |statement= | ||
| − | Если <tex>LCP(S_{Suf[x-1]} , S_{Suf[x]} ) > 1</tex>, тогда <tex>Suf^{-1}[Suf[x - 1] + 1] < Suf^{-1}[Suf[x] + 1]</tex> | + | Если <tex>LCP(S_{Suf[x-1]} , S_{Suf[x]}) > 1</tex>, тогда <tex>Suf^{-1}[Suf[x - 1] + 1] < Suf^{-1}[Suf[x] + 1]</tex> |
| + | |proof= | ||
| + | Рассмотрим пару суффиксов, соседних в массиве <tex>Suf</tex>. Тогда если их значение <tex>LCP</tex> больше <tex>1</tex>, то можно удалить первый символ этих суффиксов и их лексикографический порядок относительно друг друга сохранится. То есть строка <tex>S_{Suf[x] + 1}</tex> будет идти следом за строкой <tex>S_{Suf[x-1] + 1}</tex> и останется лексикографически больше нее. | ||
}} | }} | ||
| − | |||
| − | |||
| − | |||
{{Утверждение | {{Утверждение | ||
| + | |id = fact3 | ||
| + | |about= №3 | ||
|statement=Если <tex>LCP(S_{Suf[x-1]} , S_{Suf[x]} ) > 1</tex>, тогда <tex>LCP(S_{Suf[x-1]+1} , S_{Suf[x]+1}) = LCP(S_{Suf[x-1]} , S_{Suf[x]} ) - 1</tex> | |statement=Если <tex>LCP(S_{Suf[x-1]} , S_{Suf[x]} ) > 1</tex>, тогда <tex>LCP(S_{Suf[x-1]+1} , S_{Suf[x]+1}) = LCP(S_{Suf[x-1]} , S_{Suf[x]} ) - 1</tex> | ||
| + | |proof= | ||
| + | В этом же случае, значение <tex>LCP</tex> между <tex>S_{Suf[x-1]+1}</tex> и <tex>S_{Suf[x]+1}</tex> на один меньше значения <tex>LCP</tex> между <tex>S_{Suf[x-1]}</tex> и <tex>S_{Suf[x]}</tex>. | ||
}} | }} | ||
| + | ===Пример=== | ||
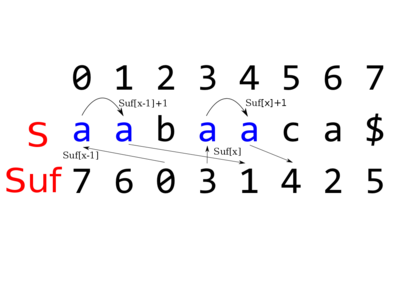
| + | [[Файл:kasai.png|400px|thumb|right|Пояснительная картинка к утверждениям 2 и 3]] | ||
| + | Рассмотрим строку <tex>S = aabaaca\$</tex>. Её суффиксный массив: | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | !<tex>i</tex> | ||
| + | | <tex>0</tex> || <tex>1</tex> || <tex>2</tex> || <tex>3</tex> || <tex>4</tex> || <tex>5</tex> || <tex>6</tex> || <tex>7</tex> | ||
| + | |- | ||
| + | !<tex>Suf[i]</tex> | ||
| + | | <tex>7</tex> || <tex>6</tex> || <tex>0</tex> || <tex>3</tex> || <tex>1</tex> || <tex>4</tex> || <tex>2</tex> || <tex>5</tex> | ||
| + | |} | ||
| + | Распишем суффиксный массив по столбикам для удобного нахождения <tex>LCP</tex>: | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | !<tex>i</tex> | ||
| + | | <tex>0</tex> || <tex>1</tex> || <tex>2</tex> || <tex>3</tex> || <tex>4</tex> || <tex>5</tex> || <tex>6</tex> || <tex>7</tex> | ||
| + | |- | ||
| + | !<tex>Suf[i]</tex> | ||
| + | | <tex>7</tex> || <tex>6</tex> || <tex>0</tex> || <tex>3</tex> || <tex>1</tex> || <tex>4</tex> || <tex>2</tex> || <tex>5</tex> | ||
| + | |- | ||
| + | !<tex>0</tex> | ||
| + | | <tex>\$</tex> || <tex>a</tex> || <tex>a</tex> || <tex>a</tex> || <tex>a</tex> || <tex>a</tex> || <tex>b</tex> || <tex>c</tex> | ||
| + | |- | ||
| + | !<tex>1</tex> | ||
| + | | || <tex>\$</tex> || <tex>a</tex> || <tex>a</tex> || <tex>b</tex> || <tex>c</tex> || <tex>a</tex> || <tex>a</tex> | ||
| + | |- | ||
| + | !<tex>2</tex> | ||
| + | | || || <tex>b</tex> || <tex>c</tex> || <tex>a</tex> || <tex>a</tex> || <tex>a</tex> || <tex>\$</tex> | ||
| + | |- | ||
| + | !<tex>3</tex> | ||
| + | | || || <tex>a</tex> || <tex>a</tex> || <tex>a</tex> || <tex>\$</tex> || <tex>c</tex> || | ||
| + | |- | ||
| + | !<tex>4</tex> | ||
| + | | || || <tex>a</tex> || <tex>\$</tex> || <tex>c</tex> || || <tex>a</tex> || | ||
| + | |- | ||
| + | !<tex>5</tex> | ||
| + | | || || <tex>c</tex> || || <tex>a</tex> || || <tex>\$</tex> || | ||
| + | |- | ||
| + | !<tex>6</tex> | ||
| + | | || || <tex>a</tex> || || <tex>\$</tex> || || || | ||
| + | |- | ||
| + | !<tex>7</tex> | ||
| + | | || || <tex>\$</tex> || || || || || | ||
| + | |} | ||
| + | Строим массив <tex>LCP</tex>: | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | !<tex>i</tex> | ||
| + | | <tex>0</tex> || <tex>1</tex> || <tex>2</tex> || <tex>3</tex> || <tex>4</tex> || <tex>5</tex> || <tex>6</tex> || <tex>7</tex> | ||
| + | |- | ||
| + | !<tex>lcp[i]</tex> | ||
| + | | <tex>\bot</tex> || <tex>0</tex> || <tex>1</tex> || <tex>2</tex> || <tex>1</tex> || <tex>1</tex> || <tex>0</tex> || <tex>0</tex> | ||
| + | |} | ||
| + | Например <tex>lcp[3] = 2</tex> {{---}} длина наибольшего общего префикса <tex>aa</tex> суффиксов <tex>S_{Suf[2]} = aabaaca\$</tex> и <tex>S_{Suf[3]} = aaca\$</tex>. | ||
===Вспомогательные утверждения=== | ===Вспомогательные утверждения=== | ||
| − | Теперь рассмотрим следующую задачу: рассчитать <tex>LCP</tex> между суффиксом <tex>S_{i}</tex> и его | + | Теперь рассмотрим следующую задачу: рассчитать <tex>LCP</tex> между суффиксом <tex>S_{i}</tex> и его соседним суффиксом в массиве <tex>Suf</tex>, при условии, что значение <tex>LCP</tex> между <tex>S_{i-1}</tex> и его соседним суффиксом известны. Для удобства записи пусть <tex>p=Suf^{-1}[i - 1]</tex> и <tex>q = Suf^{-1}[i]</tex>. Так же пусть <tex>j - 1 = Suf[p-1]</tex> и <tex>k = Suf[q - 1]</tex>. Проще говоря, мы хотим посчитать <tex>lcp[q]</tex>, когда задано <tex>lcp[p]</tex>. |
| − | {{Лемма|statement= | + | {{Лемма |
| − | Если <tex>LCP(S_{j-1}, S_{i-1}) > 1</tex>, тогда <tex>LCP(S_k,S_i) \ | + | |id = lemma |
| + | |statement= | ||
| + | Если <tex>LCP(S_{j-1}, S_{i-1}) > 1</tex>, тогда <tex>LCP(S_k,S_i) \geqslant LCP(S_j,S_i)</tex>. | ||
|proof= | |proof= | ||
| − | Так как <tex>LCP(S_{j-1},S_{i-1}) > 1</tex>, имеем <tex>Suf^{-1}[j] < Suf^{-1}[i]</tex> из | + | Так как <tex>LCP(S_{j-1},S_{i-1}) > 1</tex>, имеем <tex>Suf^{-1}[j] < Suf^{-1}[i]</tex> из [[#fact2 | утверждения №2]]. Так как <tex>Suf^{-1}[j] \leqslant Suf^{-1}[k] = Suf^{-1}[i] - 1</tex>, имеем <tex>LCP(S_{k} , S_{i}) \geqslant LCP(S_{j} , S_{i})</tex> из [[#fact1 | утверждения №1]]. |
}} | }} | ||
{{Теорема|statement= | {{Теорема|statement= | ||
| − | Если <tex> | + | Если <tex>lcp[p] = LCP(S_{j-1}, S_{i-1}) > 1</tex>, то <tex>lcp[q] = LCP(S_{k}, S_{i}) \geqslant lcp[p] - 1</tex> |
|proof= | |proof= | ||
| − | <tex>LCP(S_{k}, S_{i}) \ | + | <tex>LCP(S_{k}, S_{i}) \geqslant LCP(S_{j} , S_{i})</tex> (по [[#lemma | лемме]]). |
| + | |||
| + | <tex>LCP(S_{j} , S_{i}) = LCP(S_{j-1}, S_{i-1}) - 1</tex> (по [[#fact3 | утверждению №3]]). | ||
| + | |||
| + | Значит, <tex>LCP(S_{k}, S_{i}) \geqslant LCP(S_{j-1}, S_{i-1}) - 1</tex>. | ||
}} | }} | ||
| − | == | + | ==Алгоритм== |
| − | Таким образом, начиная проверять <tex>LCP</tex> для текущего суффикса не с первого символа, а с указанного, можно за линейное время построить <tex>LCP</tex>. | + | Представим алгоритм <tex>\mathrm{buildLCP}</tex> который вычисляет массив <tex>LCP</tex>, зная суффиксный массив. Исходя из выше написанной теоремы, нам не нужно сравнивать все символы, когда мы вычисляем <tex>LCP</tex> между суффиксом <tex>S_{i}</tex> и его соседним суффиксом в массиве <tex>Suf^{-1}</tex>. Чтобы вычислить <tex>LCP</tex> всех соседних суффиксов в массиве <tex>Suf^{-1}</tex> эффективно, будем рассматривать суффиксы по порядку начиная с <tex>S_1</tex> и заканчивая <tex>S_n</tex>. |
| − | Покажем, что построение <tex>LCP</tex> таким образом действительно требует <tex>O( | + | |
| − | чем на единицу меньше предыдущего. Таким образом, значения <tex>LCP</tex> в сумме могут увеличиться не более, чем на <tex> | + | ===Псевдокод=== |
| + | Алгоритм принимает на вход строку длиной <tex>n</tex>, с добавленным специальным символом <tex>\$</tex> и суффиксный массив этой строки, и возвращает массив <tex>lcp</tex>. | ||
| + | '''int[]''' buildLCP(str: '''string''', suf: '''int[]''') | ||
| + | '''int''' n <tex>=</tex> str.length | ||
| + | '''int[len]''' lcp | ||
| + | '''int[len]''' pos <font color=green> // pos[] {{---}} массив, обратный массиву suf </font> | ||
| + | '''for''' i = 0 '''to''' n - 1 | ||
| + | pos[suf[i]] <tex>=</tex> i | ||
| + | '''int''' k <tex>=</tex> 0 | ||
| + | '''for''' i = 0 '''to''' n - 1 | ||
| + | '''if''' k > 0 | ||
| + | k-- | ||
| + | '''if''' pos[i] == n - 1 | ||
| + | lcp[n - 1] <tex>=</tex> -1 | ||
| + | k <tex>=</tex> 0 | ||
| + | '''continue''' | ||
| + | '''else''' | ||
| + | '''int''' j <tex>=</tex> suf[pos[i] + 1] | ||
| + | '''while''' max(i + k, j + k) < n '''and''' str[i + k] == str[j + k] | ||
| + | k++ | ||
| + | lcp[pos[i]] <tex>=</tex> k | ||
| + | '''return''' lcp | ||
| + | |||
| + | ===Асимптотика=== | ||
| + | Таким образом, начиная проверять <tex>LCP</tex> для текущего суффикса не с первого символа, а с указанного, можно за линейное время построить <tex>LCP</tex>. Покажем, что построение <tex>LCP</tex> таким образом действительно требует <tex>O(n)</tex> времени. Действительно, на каждой итерации текущее значение <tex>LCP</tex> может быть не более | ||
| + | чем на единицу меньше предыдущего. Таким образом, значения <tex>LCP</tex> в сумме могут увеличиться не более, чем на <tex>2n</tex> (с точностью до константы). Следовательно, алгоритм построит <tex>LCP</tex> за <tex>O(n)</tex>. | ||
| + | |||
| + | == См. также == | ||
| + | * [[Алгоритм цифровой сортировки суффиксов циклической строки]] | ||
| − | ==Источники== | + | ==Источники информации== |
| − | + | * [[wikipedia:ru:Алгоритм_Касаи | Википедия {{---}} Алгоритм Касаи]] | |
| − | + | * [http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.118.8221 T.Kasai, G.Lee, H.Arimura, S.Arikawa, K.Park - Linear-Time Longest-Common-Prefix Computation in Suffix Arrays and Its Application] | |
[[Категория:Алгоритмы и структуры данных]] | [[Категория:Алгоритмы и структуры данных]] | ||
[[Категория:Суффиксный массив]] | [[Категория:Суффиксный массив]] | ||
Текущая версия на 19:35, 4 сентября 2022
Алгоритм Касаи, Аримуры, Арикавы, Ли, Парка (англ. Kasai, Arimura, Arikawa, Lee, Park algorithm) — алгоритм, позволяющий за линейное время вычислить длину наибольших общих префиксов (англ. longest common prefix, LCP) для всех соседних суффиксов строки, отсортированных в лексикографическом порядке.
Содержание
Обозначения
Введём следующие обозначения:
- — данная строка.
- — суффикс строки , начинающийся в -ом символе.
- — суффиксный массив.
- — массив, обратный суффиксному, который может быть получен немедленно, если задан массив . Если , то .
- — длина наибольшего общего префикса строк и .
- — длина наибольшего общего префикса соседних строк и , то есть .
Некоторые свойства LCP
| Утверждение (№1): |
|
между двумя суффиксами — минимум всех пар соседних суффиксов между ними в суффиксном массиве . То есть . Отсюда следует, что пары соседних суффиксов в массиве больше или равно пары суффиксов, окружающих их. |
Также заметим, что .
| Утверждение (№2): |
Если , тогда |
| Рассмотрим пару суффиксов, соседних в массиве . Тогда если их значение больше , то можно удалить первый символ этих суффиксов и их лексикографический порядок относительно друг друга сохранится. То есть строка будет идти следом за строкой и останется лексикографически больше нее. |
| Утверждение (№3): |
Если , тогда |
| В этом же случае, значение между и на один меньше значения между и . |
Пример
Рассмотрим строку . Её суффиксный массив:
Распишем суффиксный массив по столбикам для удобного нахождения :
Строим массив :
Например — длина наибольшего общего префикса суффиксов и .
Вспомогательные утверждения
Теперь рассмотрим следующую задачу: рассчитать между суффиксом и его соседним суффиксом в массиве , при условии, что значение между и его соседним суффиксом известны. Для удобства записи пусть и . Так же пусть и . Проще говоря, мы хотим посчитать , когда задано .
| Лемма: |
Если , тогда . |
| Доказательство: |
| Так как , имеем из утверждения №2. Так как , имеем из утверждения №1. |
| Теорема: |
Если , то |
| Доказательство: |
|
(по лемме). (по утверждению №3). Значит, . |
Алгоритм
Представим алгоритм который вычисляет массив , зная суффиксный массив. Исходя из выше написанной теоремы, нам не нужно сравнивать все символы, когда мы вычисляем между суффиксом и его соседним суффиксом в массиве . Чтобы вычислить всех соседних суффиксов в массиве эффективно, будем рассматривать суффиксы по порядку начиная с и заканчивая .
Псевдокод
Алгоритм принимает на вход строку длиной , с добавленным специальным символом и суффиксный массив этой строки, и возвращает массив .
int[] buildLCP(str: string, suf: int[]) int n str.length int[len] lcp int[len] pos // pos[] — массив, обратный массиву suf for i = 0 to n - 1 pos[suf[i]] i int k 0 for i = 0 to n - 1 if k > 0 k-- if pos[i] == n - 1 lcp[n - 1] -1 k 0 continue else int j suf[pos[i] + 1] while max(i + k, j + k) < n and str[i + k] == str[j + k] k++ lcp[pos[i]] k return lcp
Асимптотика
Таким образом, начиная проверять для текущего суффикса не с первого символа, а с указанного, можно за линейное время построить . Покажем, что построение таким образом действительно требует времени. Действительно, на каждой итерации текущее значение может быть не более чем на единицу меньше предыдущего. Таким образом, значения в сумме могут увеличиться не более, чем на (с точностью до константы). Следовательно, алгоритм построит за .