AA-дерево — различия между версиями
(→Свойства) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 22 промежуточные версии 5 участников) | |||
| Строка 3: | Строка 3: | ||
АA-дерево названо по первым буквам имени и фамилии изобретателя, Арне Андерссона, который впервые предложил данную модификацию [[Красно-черное дерево|красно-черного дерева]] в 1993 году. | АA-дерево названо по первым буквам имени и фамилии изобретателя, Арне Андерссона, который впервые предложил данную модификацию [[Красно-черное дерево|красно-черного дерева]] в 1993 году. | ||
| − | == | + | == Описание дерева == |
| + | === Структура АА-дерева === | ||
{{Определение | {{Определение | ||
| Строка 9: | Строка 10: | ||
}} | }} | ||
| + | Для представления АА-дерева в памяти будем использовать следующую структуру: | ||
| + | '''struct''' Node: | ||
| + | '''V''' value <font color="green">// значение вершины</font> | ||
| + | '''V''' level <font color="green">// высота вершины</font> | ||
| + | '''Node''' left <font color="green">// указатель на левого потомка</font> | ||
| + | '''Node''' right <font color="green">// указатель на правого потомка</font> | ||
| + | <font color=green>// Конструктор вершины (создаем экземпляр структуры с полученными значениями)</font> | ||
| + | '''Node''' (value : '''V''', level : '''V''', left : '''Node''', right: '''Node''') | ||
| + | |||
| + | === Свойства АА-дерева === | ||
| + | |||
| + | Свойства АА-дерева: | ||
| + | *Уровень каждого листа равен <tex>1</tex>. | ||
| + | *Уровень каждого левого ребенка ровно на один меньше, чем у его родителя. | ||
| + | *Уровень каждого правого ребенка равен или на один меньше, чем у его родителя. | ||
| + | *Уровень каждого правого внука строго меньше, чем у его прародителя. | ||
| + | *Каждая вершина с уровнем больше <tex>1</tex> имеет двоих детей. | ||
| + | |||
| + | === Связь с красно-чёрным деревом === | ||
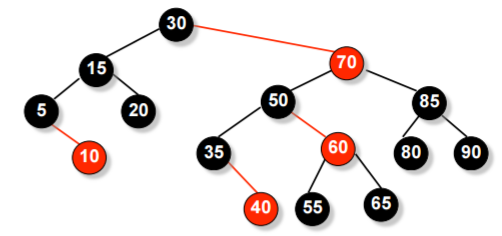
В отличие от красно-черных деревьев, к одной вершине можно присоединить вершину только того же уровня, только одну и только справа (другими словами, красные вершины могут быть добавлены только в качестве правого ребенка). На картинке ниже представлен пример красно-чёрного дерева. | В отличие от красно-черных деревьев, к одной вершине можно присоединить вершину только того же уровня, только одну и только справа (другими словами, красные вершины могут быть добавлены только в качестве правого ребенка). На картинке ниже представлен пример красно-чёрного дерева. | ||
| Строка 21: | Строка 41: | ||
[[Файл: Exaa2.PNG]] | [[Файл: Exaa2.PNG]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Для поддержки баланса красно-черного дерева необходимо обрабатывать <tex>7</tex> различных вариантов расположения вершин: | Для поддержки баланса красно-черного дерева необходимо обрабатывать <tex>7</tex> различных вариантов расположения вершин: | ||
| Строка 33: | Строка 46: | ||
[[Файл: Rb3.png]] | [[Файл: Rb3.png]] | ||
| − | В АА-дереве из-за строгих ограничений необходимо обрабатывать только два вида возможных расположений вершин | + | В АА-дереве из-за строгих ограничений необходимо обрабатывать только два вида возможных расположений вершин, чтобы проверить соблюдается ли главное правило «одна правая горизонтальная связь». То есть мы должны проверить нет ли левой горизонтальной связи, как на первом рисунке ниже и нет ли двух последовательных правых горизонтальных связей, как на правом рисунке. |
| − | |||
| − | |||
| − | + | [[Файл: Pr1.png]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Балансировка == | == Балансировка == | ||
| Строка 71: | Строка 71: | ||
'''else''' '''if''' t.left == <tex>\varnothing</tex> | '''else''' '''if''' t.left == <tex>\varnothing</tex> | ||
'''return''' t | '''return''' t | ||
| + | <font color=green>// Проверяем, есть ли у нас левое горизонтальное ребро</font> | ||
'''else''' '''if''' t.left.level == t.level | '''else''' '''if''' t.left.level == t.level | ||
<font color=green>// Меняем указатель горизонтального левого ребра</font> | <font color=green>// Меняем указатель горизонтального левого ребра</font> | ||
| − | + | '''return''' Node(t.left, t.left.level, t.left.left, Node(t, t.level, t.left.right, t.right)) | |
| − | |||
| − | |||
| − | |||
'''else''' | '''else''' | ||
'''return''' t | '''return''' t | ||
| Строка 91: | Строка 89: | ||
'''if''' t == <tex>\varnothing</tex> | '''if''' t == <tex>\varnothing</tex> | ||
'''return''' <tex>\varnothing</tex> | '''return''' <tex>\varnothing</tex> | ||
| − | '''else''' '''if''' t.right == <tex>\varnothing</tex> '''or''' | + | '''else''' '''if''' t.right == <tex>\varnothing</tex> '''or''' t.right.right == <tex>\varnothing</tex> |
'''return''' t | '''return''' t | ||
| + | <font color=green>// Проверяем, один ли уровень у родителя и внука, т.е. существует ли два последовательных правых горизонтальных ребра</font> | ||
'''else''' '''if''' t.level == t.right.right.level | '''else''' '''if''' t.level == t.right.right.level | ||
| − | <font color=green> // Существует два правых горизонтальных ребра. Берем центральную вершину, | + | <font color=green>// Существует два правых горизонтальных ребра. Берем центральную вершину, «поднимаем» ее и возвращаем указатель на нее</font> |
| − | + | '''return''' Node(t.right, t.right.level + 1, Node(t, t.level, t.left, t.right.left), t.right.right) | |
| − | |||
| − | |||
| − | |||
| − | |||
'''else''' | '''else''' | ||
'''return''' t | '''return''' t | ||
| Строка 120: | Строка 115: | ||
t.right = insert(x, t.right) | t.right = insert(x, t.right) | ||
<font color=green>// Случай x == t.value не определен. Т.е. вставка не будет иметь никакого эффекта, | <font color=green>// Случай x == t.value не определен. Т.е. вставка не будет иметь никакого эффекта, | ||
| − | возможны различные варианты обработки, в зависимости от решаемой задачи</font> | + | // возможны различные варианты обработки, в зависимости от решаемой задачи</font> |
t = skew(t) | t = skew(t) | ||
t = split(t) | t = split(t) | ||
| Строка 130: | Строка 125: | ||
=== Удаление вершины === | === Удаление вершины === | ||
| − | Как и в большинстве сбалансированных бинарных деревьев, удаление внутренней вершины можно заменить на удаление листа, если заменить внутреннюю вершину на ее ближайшего «предшественника» или «преемника», в зависимости от реализации. «Предшественник» | + | Как и в большинстве сбалансированных бинарных деревьев, удаление внутренней вершины можно заменить на удаление листа, если заменить внутреннюю вершину на ее ближайшего «предшественника» или «преемника», в зависимости от реализации. «Предшественник» находится в начале последнего левого ребра, после которого идут все правые ребра. По аналогии, «преемник» может быть найден после одного правого ребра и последовательности левых ребер, пока не будет найден указатель на NULL. В силу свойства всех узлов уровня более чем <tex>1</tex>, имеющих двух детей, предшественник или преемник будет на уровне <tex>1</tex>, что делает их удаление тривиальным. Ниже представлена рекурсивная реализация алгоритма. |
Будем использовать дополнительную функцию <tex>\mathrm{decreaseLevel}</tex>, она будет обновлять уровень вершины, которую передают в функцию, в зависимости от значения уровня дочерних вершин. | Будем использовать дополнительную функцию <tex>\mathrm{decreaseLevel}</tex>, она будет обновлять уровень вершины, которую передают в функцию, в зависимости от значения уровня дочерних вершин. | ||
| Строка 157: | Строка 152: | ||
'''else''' '''if''' t.left == <tex>\varnothing</tex> | '''else''' '''if''' t.left == <tex>\varnothing</tex> | ||
l = successor(t) | l = successor(t) | ||
| − | t.right = delete | + | t.right = delete(l.valuel, t.right) |
t.value = l.value | t.value = l.value | ||
'''else''' | '''else''' | ||
| − | l | + | l = predecessor(t) |
| − | t.left = delete(l.value, t.left | + | t.left = delete(l.value, t.left) |
t.value = l.value | t.value = l.value | ||
| − | <font color=green>// Сбалансируем дерево. Если необходимо, уменьшим поля | + | <font color=green>// Сбалансируем дерево. Если необходимо, уменьшим поля «уровень» |
| − | у вершин на данном уровне, и затем skew и split все вершины на новом уровне</font> | + | // у вершин на данном уровне, и затем skew и split все вершины на новом уровне</font> |
t = decreaseLevel(t) | t = decreaseLevel(t) | ||
t = skew(t) | t = skew(t) | ||
t.right = skew(t.right) | t.right = skew(t.right) | ||
| − | '''if | + | '''if''' t.right <tex> \neq\ \varnothing</tex> |
t.right.right = skew(t.right.right) | t.right.right = skew(t.right.right) | ||
t = split(t) | t = split(t) | ||
| Строка 179: | Строка 174: | ||
== Эффективность == | == Эффективность == | ||
| − | Оценка на высоту деревьев соответствует оценке для красно-черного дерева, <tex>2\cdot log 2(N)</tex>, так как AA-дерево сохраняет структуру красно-черного дерева. Следовательно все операции происходят за <tex>O(log N)</tex>, потому что в сбалансированном двоичном дереве поиска почти все операции реализуются за <tex>O(h)</tex>. Скорость работы AA-дерева эквивалентна скорости работы красно-черного дерева, но так как в реализации вместо цвета обычно хранят «уровень» вершины, | + | Оценка на высоту деревьев соответствует оценке для красно-черного дерева, <tex>2\cdot \log 2(N)</tex>, так как AA-дерево сохраняет структуру красно-черного дерева. Следовательно все операции происходят за <tex>O(\log N)</tex>, потому что в сбалансированном двоичном дереве поиска почти все операции реализуются за <tex>O(h)</tex>. Скорость работы AA-дерева эквивалентна скорости работы красно-черного дерева, но так как в реализации вместо цвета обычно хранят «уровень» вершины, дополнительные расходы по памяти достигают байта. |
== См. также == | == См. также == | ||
Текущая версия на 19:36, 4 сентября 2022
АA-дерево (англ. AA-Tree) — структура данных, представляющая собой сбалансированное двоичное дерево поиска, которое является разновидностью красно-черного дерева с дополнительными ограничениями.
АA-дерево названо по первым буквам имени и фамилии изобретателя, Арне Андерссона, который впервые предложил данную модификацию красно-черного дерева в 1993 году.
Содержание
Описание дерева
Структура АА-дерева
| Определение: |
| Уровень вершины (англ. Level) — вертикальная высота соответствующей вершины. |
Для представления АА-дерева в памяти будем использовать следующую структуру:
struct Node: V value // значение вершины V level // высота вершины Node left // указатель на левого потомка Node right // указатель на правого потомка // Конструктор вершины (создаем экземпляр структуры с полученными значениями) Node (value : V, level : V, left : Node, right: Node)
Свойства АА-дерева
Свойства АА-дерева:
- Уровень каждого листа равен .
- Уровень каждого левого ребенка ровно на один меньше, чем у его родителя.
- Уровень каждого правого ребенка равен или на один меньше, чем у его родителя.
- Уровень каждого правого внука строго меньше, чем у его прародителя.
- Каждая вершина с уровнем больше имеет двоих детей.
Связь с красно-чёрным деревом
В отличие от красно-черных деревьев, к одной вершине можно присоединить вершину только того же уровня, только одну и только справа (другими словами, красные вершины могут быть добавлены только в качестве правого ребенка). На картинке ниже представлен пример красно-чёрного дерева.
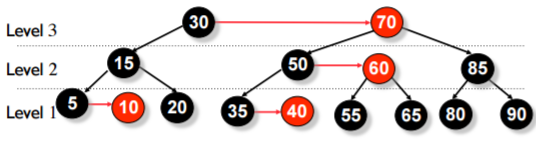
Теперь рассмотрим то же дерево, но с информацией об уровне каждой вершине. Горизонтальные ребра обозначают связи между ребрами одного уровня.
На практике в AA-дереве вместо значения цвета для балансировки дерева в вершине хранится информация только о ее уровне.
Для поддержки баланса красно-черного дерева необходимо обрабатывать различных вариантов расположения вершин:
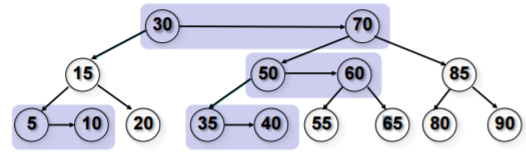
В АА-дереве из-за строгих ограничений необходимо обрабатывать только два вида возможных расположений вершин, чтобы проверить соблюдается ли главное правило «одна правая горизонтальная связь». То есть мы должны проверить нет ли левой горизонтальной связи, как на первом рисунке ниже и нет ли двух последовательных правых горизонтальных связей, как на правом рисунке.
Балансировка
| Определение: |
| Горизонтальное ребро (англ. Horizontal edges) — ребро, соединяющее вершины с одинаковым уровнем. |
В AA-дереве разрешены правые ребра, не идущие подряд, и запрещены все левые горизонтальные ребра.
Эти более жесткие ограничения , аналогичные ограничениям на красно-черных деревьях, приводят к более простой реализации балансировки AA-дерева.
Для балансировки АА-дерева нужны следующие две операции:
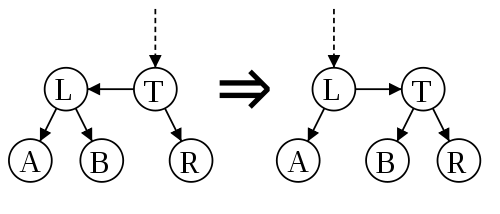
Skew
— устранение левого горизонтального ребра. Делаем правое вращение, чтобы заменить поддерево, содержащее левую горизонтальную связь, на поддерево, содержащее разрешенную правую горизонтальную связь.
Node skew(t : Node) if t == return else if t.left == return t // Проверяем, есть ли у нас левое горизонтальное ребро else if t.left.level == t.level // Меняем указатель горизонтального левого ребра return Node(t.left, t.left.level, t.left.left, Node(t, t.level, t.left.right, t.right)) else return t
На рисунке ниже представлен пример работы алгоритма.
Split
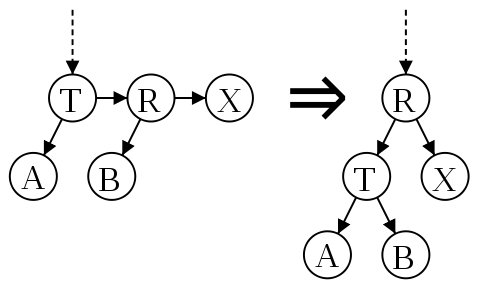
— устранение двух последовательных правых горизонтальных ребер. Делаем левое вращение и увеличиваем уровень, чтобы заменить поддерево, содержащее две или более последовательных правильных горизонтальных связи, на вершину, содержащую два поддерева с меньшим уровнем.
Node split(t : Node) if t == return else if t.right == or t.right.right == return t // Проверяем, один ли уровень у родителя и внука, т.е. существует ли два последовательных правых горизонтальных ребра else if t.level == t.right.right.level // Существует два правых горизонтальных ребра. Берем центральную вершину, «поднимаем» ее и возвращаем указатель на нее return Node(t.right, t.right.level + 1, Node(t, t.level, t.left, t.right.left), t.right.right) else return t
На рисунке ниже представлен пример работы алгоритма.
Операции
Вставка элемента
Вставка нового элемента происходит как в обычном дереве поиска, только на пути вверх необходимо делать ребалансировку, используя и . Ниже представлена рекурсивная реализация алгоритма.
Node insert(x : V, t : Node) // x — вставляемое значение, t — корень дерева, в который вставляется вершина if t == return Node(x, 1, , ) else if x < t.value t.left = insert(x, t.left) else if x > t.value t.right = insert(x, t.right) // Случай x == t.value не определен. Т.е. вставка не будет иметь никакого эффекта, // возможны различные варианты обработки, в зависимости от решаемой задачи t = skew(t) t = split(t) return t
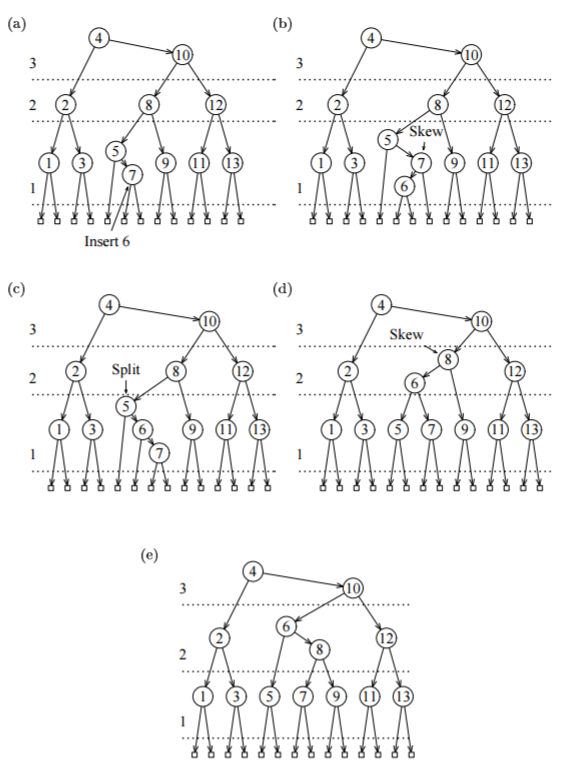
Пример вставки нового элемента (на рис. уровни разделены горизонтальными линиями):
Удаление вершины
Как и в большинстве сбалансированных бинарных деревьев, удаление внутренней вершины можно заменить на удаление листа, если заменить внутреннюю вершину на ее ближайшего «предшественника» или «преемника», в зависимости от реализации. «Предшественник» находится в начале последнего левого ребра, после которого идут все правые ребра. По аналогии, «преемник» может быть найден после одного правого ребра и последовательности левых ребер, пока не будет найден указатель на NULL. В силу свойства всех узлов уровня более чем , имеющих двух детей, предшественник или преемник будет на уровне , что делает их удаление тривиальным. Ниже представлена рекурсивная реализация алгоритма.
Будем использовать дополнительную функцию , она будет обновлять уровень вершины, которую передают в функцию, в зависимости от значения уровня дочерних вершин.
Node decreaseLevel(t : Node)
shouldBe = min(t.left.level, t.right.level) + 1
if shouldBe < t.level
t.level = shouldBe
if shouldBe < t.right.level
t.right.level = shouldBe
return t
Чтобы сохранять баланс дерева необходимо делать , и для каждой вершины.
Node delete(x : V, t : Node) // x — удаляемый элемент, t — корень дерева, из которого он должен быть удален if t == return t else if x > t.value t.right = delete(x, t.right) else if x < t.value t.left = delete(x, t.left) else if leaf(t) return else if t.left == l = successor(t) t.right = delete(l.valuel, t.right) t.value = l.value else l = predecessor(t) t.left = delete(l.value, t.left) t.value = l.value // Сбалансируем дерево. Если необходимо, уменьшим поля «уровень» // у вершин на данном уровне, и затем skew и split все вершины на новом уровне t = decreaseLevel(t) t = skew(t) t.right = skew(t.right) if t.right t.right.right = skew(t.right.right) t = split(t) t.right = split(t.right) return t
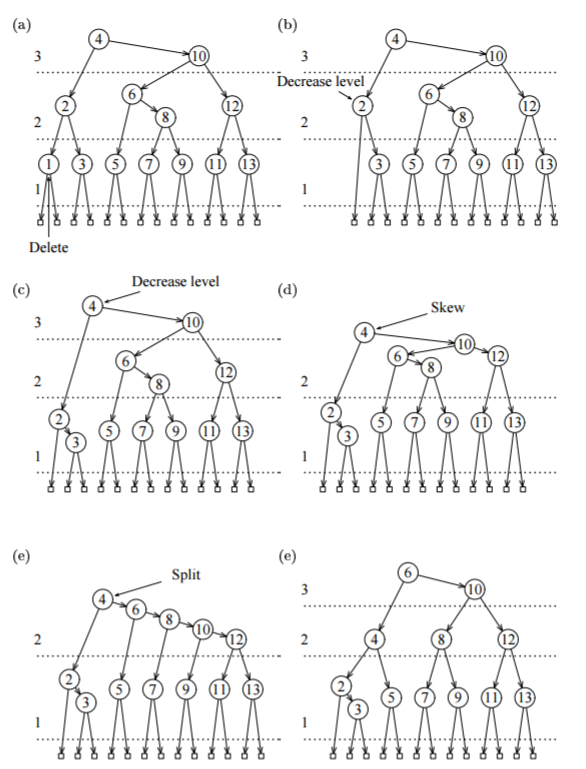
Пример удаления вершины (на рис. уровни разделены горизонтальными линиями):
Эффективность
Оценка на высоту деревьев соответствует оценке для красно-черного дерева, , так как AA-дерево сохраняет структуру красно-черного дерева. Следовательно все операции происходят за , потому что в сбалансированном двоичном дереве поиска почти все операции реализуются за . Скорость работы AA-дерева эквивалентна скорости работы красно-черного дерева, но так как в реализации вместо цвета обычно хранят «уровень» вершины, дополнительные расходы по памяти достигают байта.