Матрица инцидентности графа — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
м (rollbackEdits.php mass rollback)
 
(не показано 17 промежуточных версий 8 участников)
Строка 1: Строка 1:
−
== Инцидентность ребра и вершины ==
+
== Определения для ориентированного и неориентированного графов ==
  
 
{{Определение
 
{{Определение
 
|definition=
 
|definition=
−
'''Инцидентность''' - отношение между ребром и его концевыми вершинами, т. е. если в графе <math>G = (V,E) </math>   <math>u \in V, v \in V</math> - вершины, а <math>e \in E</math> - соединяющее их ребро (e = (u,v)), то вершина u и ребро e инцидентны, вершина v и ребро e также инцидентны.
+
'''Матрицей инцидентности''' (инциденций) ''(англ. Incidence matrix)'' неориентированного графа называется матрица <tex>I (|V| \times |E|)</tex>, для которой <tex>I_{i,j} = 1</tex>, если вершина <tex>v_i</tex> инцидентна ребру <tex>e_j</tex>, в противном случае <tex>I_{i,j} = 0</tex>.
 
}}
 
}}
−
 
−
== Определения для ориентированного и неориентированного графов ==
 
  
 
{{Определение
 
{{Определение
 
|definition=
 
|definition=
−
'''Матрицей инцидентности''' (инциденций) неориентированного графа называется матрица <math>I (V \times E)</math>, (i, j)-й элемент которой равен 1, если вершина <math>v_i</math> инцидентна ребру <math>e_j</math>, и 0 в противном случае.
+
'''Матрицей инцидентности''' (инциденций) ''(англ. Incidence matrix)'' ориентированного графа называется матрица <tex>I (|V| \times |E|)</tex>, для которой <tex>I_{i,j} = 1</tex>, если вершина <tex>v_i</tex> является началом дуги <tex>e_j</tex>, <tex>I_{i,j} = -1</tex>, если <tex>v_i</tex> является концом дуги <tex>e_j</tex>, в остальных случаях <tex>I_{i,j} = 0</tex>.
 +
}}
 +
 
 +
== Свойства ==
 +
{{Утверждение
 +
|statement=Для неориентированных графов без петель и кратных рёбер матрица инцидентности бинарна (состоит из нулей и единиц).
 +
}}
 +
 
 +
{{Утверждение
 +
|statement=Для ориентированных графов без петель и кратных рёбер матрица инцидентности состоит из нулей, единиц и <tex>-1</tex>.
 
}}
 
}}
  
−
{{Определение
+
{{Утверждение
−
|definition=
+
|about=о сумме элементов строки матрицы инцидентности для неориентированного графа
−
'''Матрицей инцидентности''' (инциденций) ориентированного графа называется матрица <math>I (V \times E)</math>, (i, j)-й элемент которой равен 1, если вершина <math>v_i</math> является началом дуги <math>e_j</math>, -1, если <math>v_i</math> является концом дуги <math>e_j</math>, и 0 в остальных случаях.
+
|statement=Сумма элементов <tex>i</tex>-й строки равна <tex>deg \; v_i</tex>.
 +
}}
 +
 
 +
{{Утверждение
 +
|about=о сумме элементов строки матрицы инцидентности для ориентированного графа
 +
|statement=Сумма элементов <tex>i</tex>-й строки равна <tex>deg^+ v_i - deg^- v_i</tex>.
 
}}
 
}}
 +
 +
== Пример ==
 +
{| border="1" cellpadding="5" cellspacing="0" style="text-align:center"
 +
!style="background:#f2f2f2"|Граф
 +
!style="background:#f2f2f2"|Матрица инцидентности
 +
!style="background:#f2f2f2"|Ориентированный граф
 +
!style="background:#f2f2f2"|Матрица инцидентности
 +
|-
 +
|style="background:#f9f9f9"|[[Файл:incidence_matrix_undirected_graph.png|200px]]
 +
|style="background:#f9f9f9"|<tex>\begin{pmatrix}
 +
1 & 1 & 1 & 0 & 1 & 0\\
 +
1 & 0 & 0 & 1 & 0 & 0\\
 +
0 & 1 & 0 & 0 & 0 & 1\\
 +
0 & 0 & 1 & 0 & 0 & 1\\
 +
0 & 0 & 0 & 1 & 1 & 0\\
 +
\end{pmatrix}</tex>
 +
|style="background:#f9f9f9"|[[Файл:incidence_matrix_directed_graph.png|200px]]
 +
|style="background:#f9f9f9"|<tex>\begin{pmatrix}
 +
-1 & 1 & -1 & 0 & -1 & 0\\
 +
1 & 0 & 0 & -1 & 0 & 0\\
 +
0 & -1 & 0 & 0 & 0 & 1\\
 +
0 & 0 & 1 & 0 & 0 & -1\\
 +
0 & 0 & 0 & 1 & 1 & 0\\
 +
\end{pmatrix}</tex>
 +
|}
 +
 +
== См. также ==
 +
* [[Матрица смежности графа]]
 +
 +
==Источники==
 +
* Харари Фрэнк :'''Теория графов'''. Под ред. Л. Б. Штейнпресс. Изд. 2-е. — М.: Мир, 1973. — 180 с. — ISBN 5-354-00301-6
 +
* Асанов М. О., Баранский В. А., Расин В. В.: '''Дискретная математика: графы, матроиды, алгоритмы''' — НИЦ РХД, 2001. — 288 с. — ISBN 5-93972-076-5
 +
* [https://en.wikipedia.org/wiki/Incidence_matrix Википедия {{---}} Incidence matrix]
 +
 +
[[Категория: Алгоритмы и структуры данных]]
 +
[[Категория: Основные определения теории графов]]

Текущая версия на 19:36, 4 сентября 2022

Определения для ориентированного и неориентированного графов

Определение:
Матрицей инцидентности (инциденций) (англ. Incidence matrix) неориентированного графа называется матрица [math]I (|V| \times |E|)[/math], для которой [math]I_{i,j} = 1[/math], если вершина [math]v_i[/math] инцидентна ребру [math]e_j[/math], в противном случае [math]I_{i,j} = 0[/math].


Определение:
Матрицей инцидентности (инциденций) (англ. Incidence matrix) ориентированного графа называется матрица [math]I (|V| \times |E|)[/math], для которой [math]I_{i,j} = 1[/math], если вершина [math]v_i[/math] является началом дуги [math]e_j[/math], [math]I_{i,j} = -1[/math], если [math]v_i[/math] является концом дуги [math]e_j[/math], в остальных случаях [math]I_{i,j} = 0[/math].


Свойства

Утверждение:
Для неориентированных графов без петель и кратных рёбер матрица инцидентности бинарна (состоит из нулей и единиц).
Утверждение:
Для ориентированных графов без петель и кратных рёбер матрица инцидентности состоит из нулей, единиц и [math]-1[/math].
Утверждение (о сумме элементов строки матрицы инцидентности для неориентированного графа):
Сумма элементов [math]i[/math]-й строки равна [math]deg \; v_i[/math].
Утверждение (о сумме элементов строки матрицы инцидентности для ориентированного графа):
Сумма элементов [math]i[/math]-й строки равна [math]deg^+ v_i - deg^- v_i[/math].

Пример

Граф Матрица инцидентности Ориентированный граф Матрица инцидентности
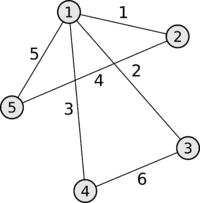
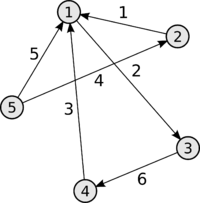
Incidence matrix undirected graph.png [math]\begin{pmatrix} 1 & 1 & 1 & 0 & 1 & 0\\ 1 & 0 & 0 & 1 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0 & 0 & 1\\ 0 & 0 & 0 & 1 & 1 & 0\\ \end{pmatrix}[/math] Incidence matrix directed graph.png [math]\begin{pmatrix} -1 & 1 & -1 & 0 & -1 & 0\\ 1 & 0 & 0 & -1 & 0 & 0\\ 0 & -1 & 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0 & 0 & -1\\ 0 & 0 & 0 & 1 & 1 & 0\\ \end{pmatrix}[/math]

См. также

Источники

  • Харари Фрэнк :Теория графов. Под ред. Л. Б. Штейнпресс. Изд. 2-е. — М.: Мир, 1973. — 180 с. — ISBN 5-354-00301-6
  • Асанов М. О., Баранский В. А., Расин В. В.: Дискретная математика: графы, матроиды, алгоритмы — НИЦ РХД, 2001. — 288 с. — ISBN 5-93972-076-5
  • Википедия — Incidence matrix
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Матрица_инцидентности_графа&oldid=85620»