Сведение задачи RMQ к задаче LCA — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 25 промежуточных версий 8 участников) | |||
| Строка 1: | Строка 1: | ||
| − | = | + | {{Шаблон:Задача |
| − | Дан массив <tex>A[1..N]</tex>. Поступают запросы вида <tex>(i, j)</tex>, на каждый запрос требуется найти минимум в массиве <tex>A</tex>, начиная с позиции <tex>i</tex> и заканчивая позицией <tex>j</tex>. | + | |definition =Дан массив <tex>A[1..N]</tex>. Поступают запросы вида <tex>(i, j)</tex>, на каждый запрос требуется найти минимум в массиве <tex>A</tex>, начиная с позиции <tex>i</tex> и заканчивая позицией <tex>j</tex>. |
| + | }} | ||
| + | |||
== Алгоритм == | == Алгоритм == | ||
| − | [[Файл:Wiki.PNG|thumb|right| | + | ===Описание=== |
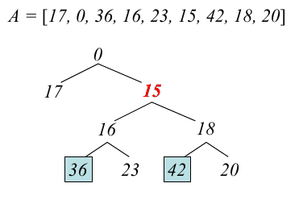
| − | Декартово дерево | + | [[Файл:Wiki.PNG|thumb|right|400x200px|Пример декартового дерева]] |
| − | * Корнем дерева является минимальное значение | + | Будем решать задачу RMQ, уже умея решать задачу LCA. Для хранения решения задачи о LCA будем использовать [[декартово дерево по неявному ключу]]. Тогда минимум на отрезке от <tex> i </tex> до <tex> j </tex> массива <tex> A </tex> будет равен наименьшему общему предку <tex>i</tex>-того и <tex>j</tex>-того элементов из декартова дерева, построенного на массиве <tex> A </tex>. |
| + | |||
| + | |||
| + | Декартово дерево по неявному ключу на массиве <tex>A[1..N]</tex> {{---}} это бинарное дерево, допускающее следующее рекурсивное построение: | ||
| + | * Корнем дерева является элемент массива, имеющий минимальное значение <tex>A</tex>, скажем <tex>A[i]</tex>. Если минимальных элементов несколько, можно взять любой. | ||
* Левым поддеревом является декартово дерево на массиве <tex>A[1..i-1]</tex>. | * Левым поддеревом является декартово дерево на массиве <tex>A[1..i-1]</tex>. | ||
* Правым поддеревом является декартово дерево на массиве <tex>A[i+1..N]</tex>. | * Правым поддеревом является декартово дерево на массиве <tex>A[i+1..N]</tex>. | ||
| + | |||
| + | Здесь и далее <tex>A[i]</tex> будет также использоваться для обозначения соответствующей вершины дерева. | ||
| + | |||
Построим декартово дерево на массиве <tex>A</tex>. Тогда <tex>RMQ(i, j)</tex> = <tex>LCA(A[i], A[j])</tex>. | Построим декартово дерево на массиве <tex>A</tex>. Тогда <tex>RMQ(i, j)</tex> = <tex>LCA(A[i], A[j])</tex>. | ||
| − | == | + | <br clear="all"> |
| − | + | ||
| − | + | === Корректность === | |
| − | + | {{Теорема | |
| − | == Сложность == | + | |statement= |
| − | Построение дерева | + | <tex>RMQ(i, j)</tex> = <tex>LCA(A[i], A[j])</tex>. |
| + | |proof= | ||
| + | Положим <tex>w = LCA(A[i], A[j])</tex>. | ||
| + | |||
| + | Заметим, что <tex>A[i]</tex> и <tex>A[j]</tex> не принадлежат одновременно либо правому, либо левому поддереву <tex>w</tex>, потому как тогда бы соответствующий сын находился на большей глубине, чем <tex>w</tex>, и также являлся предком как <tex>A[i]</tex>, так и <tex>A[j]</tex>, что противоречит определению <tex>LCA</tex>. Из этого замечания следует, что <tex>w</tex> лежит между <tex>A[i]</tex> и <tex>A[j]</tex> и, следовательно, принадлежит отрезку <tex>A[i..j]</tex>. | ||
| + | |||
| + | |||
| + | По построению мы также знаем, что: | ||
| + | # Любая вершина дерева имеет свое значение меньшим либо равным значению её детей. | ||
| + | # Поддерево с корнем в <tex>w</tex> содержит в себе подмассив <tex>A[i..j]</tex>. | ||
| + | |||
| + | Суммируя, получаем, что <tex>w</tex> имеет минимальное значение на отрезке, покрывающем <tex>A[i..j]</tex>, и принадлежит отрезку <tex>A[i..j]</tex>, отсюда <tex>RMQ(i, j) = w</tex>. | ||
| + | }} | ||
| + | |||
| + | === Сложность === | ||
| + | Существует [[Декартово дерево#Построение декартова дерева|алгоритм]], который строит декартово дерево за <tex>O(n)</tex>. Используя [[Сведение задачи LCA к задаче RMQ | алгоритм построения LCA]], получаем: | ||
| + | препроцессинг для <tex>LCA</tex> {{---}} <tex>O(n)</tex> и ответ на запрос {{---}} <tex>O(1)</tex>. | ||
| + | |||
| + | Нам нужно единожды построить декартово дерево за <tex>O(n)</tex>, единожды провести препроцессинг за <tex>O(n)</tex> и отвечать на запросы за <tex>O(1)</tex>. | ||
| + | |||
| + | В итоге получили <tex>RMQ</tex> с построением за <tex>O(n)</tex> и ответом на запрос за <tex>O(1)</tex>. | ||
| − | |||
| − | |||
== См.также == | == См.также == | ||
*[[Сведение задачи LCA к задаче RMQ]] | *[[Сведение задачи LCA к задаче RMQ]] | ||
| + | *[[Декартово дерево]] | ||
| + | *[[Алгоритм Фарака-Колтона и Бендера]] | ||
| + | |||
| + | [[Категория: Алгоритмы и структуры данных]] | ||
| + | [[Категория: Задача о наименьшем общем предке]] | ||
Текущая версия на 19:36, 4 сентября 2022
| Задача: |
| Дан массив . Поступают запросы вида , на каждый запрос требуется найти минимум в массиве , начиная с позиции и заканчивая позицией . |
Алгоритм
Описание
Будем решать задачу RMQ, уже умея решать задачу LCA. Для хранения решения задачи о LCA будем использовать декартово дерево по неявному ключу. Тогда минимум на отрезке от до массива будет равен наименьшему общему предку -того и -того элементов из декартова дерева, построенного на массиве .
Декартово дерево по неявному ключу на массиве — это бинарное дерево, допускающее следующее рекурсивное построение:
- Корнем дерева является элемент массива, имеющий минимальное значение , скажем . Если минимальных элементов несколько, можно взять любой.
- Левым поддеревом является декартово дерево на массиве .
- Правым поддеревом является декартово дерево на массиве .
Здесь и далее будет также использоваться для обозначения соответствующей вершины дерева.
Построим декартово дерево на массиве . Тогда = .
Корректность
| Теорема: |
= . |
| Доказательство: |
|
Положим . Заметим, что и не принадлежат одновременно либо правому, либо левому поддереву , потому как тогда бы соответствующий сын находился на большей глубине, чем , и также являлся предком как , так и , что противоречит определению . Из этого замечания следует, что лежит между и и, следовательно, принадлежит отрезку .
|
Сложность
Существует алгоритм, который строит декартово дерево за . Используя алгоритм построения LCA, получаем: препроцессинг для — и ответ на запрос — .
Нам нужно единожды построить декартово дерево за , единожды провести препроцессинг за и отвечать на запросы за .
В итоге получили с построением за и ответом на запрос за .