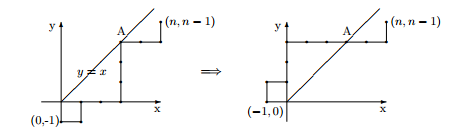Числа Каталана — различия между версиями
Novik (обсуждение | вклад) (→Подсчет чисел Каталана) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 79 промежуточных версий 6 участников) | |||
| Строка 4: | Строка 4: | ||
|id = def1 | |id = def1 | ||
|definition ='''Числа Каталана''' {{---}} последовательность чисел, выражающих: | |definition ='''Числа Каталана''' {{---}} последовательность чисел, выражающих: | ||
| − | *количество не изоморфных упорядоченных бинарных деревьев с корнем и <tex dpi = 120> n + 1 </tex> листьями | + | *количество [[Дерево_поиска,_наивная_реализация|не изоморфных упорядоченных бинарных деревьев]] с корнем и <tex dpi = 120> n + 1 </tex> листьями |
*количество способов соединения <tex dpi = 120> 2n </tex> точек на окружности <tex dpi = 120> n </tex> не пересекающимися хордами | *количество способов соединения <tex dpi = 120> 2n </tex> точек на окружности <tex dpi = 120> n </tex> не пересекающимися хордами | ||
| − | *количество триангуляций выпуклого <tex dpi = 120> n </tex>-угольника | + | *количество [[Триангуляция_полигонов_(ушная_%2B_монотонная)|триангуляций выпуклого <tex dpi = 120> n </tex>-угольника]] |
*количество способов полностью разделить скобками <tex dpi = 120> n + 1 </tex> множитель | *количество способов полностью разделить скобками <tex dpi = 120> n + 1 </tex> множитель | ||
| − | *количество корректных скобочных последовательностей, состоящих из <tex dpi = 120> n </tex> открывающих и <tex dpi = 120> n </tex> закрывающих скобок}} | + | *количество [[Правильные_скобочные_последовательности|корректных скобочных последовательностей, состоящих из <tex dpi = 120> n </tex> открывающих и <tex dpi = 120> n </tex> закрывающих скобок]] |
| + | *количество таблиц Юнга размером <tex dpi = 120>2n</tex> | ||
| + | *количество монотонных путей в квадрате размером <tex dpi = 120>n \times n</tex>, не пересекающих диагональ | ||
| + | *количество способов расставить скобки в произведении <tex dpi = 120>n</tex> множителей | ||
| + | *количество способов заполнить лестницу ширины и высоты <tex dpi = 120>n</tex> прямоугольниками | ||
| + | и так далее}} | ||
| − | Первые несколько чисел Каталана: | + | Первые несколько чисел Каталана: |
| − | <tex dpi = 120> 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, | + | <tex dpi = 120> 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, \ldots </tex> |
| − | == | + | ==Формулы вычисления чисел Каталана== |
| − | <tex dpi = 150>C_n = \ | + | ===Рекуррентная формула=== |
| + | <tex dpi = 150>C_n = \sum\limits_{i = 0}^{n - 1} C_i C_{n - 1 - i} </tex> | ||
====Доказательство==== | ====Доказательство==== | ||
Рекуррентную формулу легко вывести из задачи о правильных скобочных последовательностях. | Рекуррентную формулу легко вывести из задачи о правильных скобочных последовательностях. | ||
| − | + | Пусть <tex dpi = 120>X</tex> — произвольная правильная скобочная последовательность длины <tex dpi = 120>2n</tex>. Она начинается с открывающейся скобки. Найдем парную ей закрывающуюся скобку и представим последовательность <tex dpi = 120>X</tex> в виде: <tex dpi = 120>X = (A)B</tex>, где <tex dpi = 120>A</tex> и <tex dpi = 120>B</tex> — тоже правильные скобочные последовательности. Если длина последовательности <tex dpi = 120>A</tex> равна <tex dpi = 120>2k</tex>, то последовательность <tex dpi = 120>A</tex> можно составить <tex dpi = 120>C_k</tex> способами. Тогда длина последовательности <tex dpi = 120>B</tex> равна <tex dpi = 120>2(n - k - 1)</tex> и последовательность <tex dpi =120>B</tex> можно составить <tex dpi = 120>C_{n - k - 1}</tex> способами. Комбинация любого способа составить последовательность <tex dpi = 120>A</tex> с любым способом составить последовательность <tex dpi = 120>B</tex> даст новую последовательность <tex dpi = 120>X</tex>, а величина <tex dpi = 120>k</tex> может меняться от <tex dpi = 120>0</tex> до <tex dpi = 120>n - 1</tex>. Получили рекуррентное соотношение: <tex dpi = 120>C_n = C_0 C_{n-1} + C_1 C_{n-2} + \ldots + C_{n-1} C_0 </tex>. Так как <tex dpi = 120>C_0 = 1</tex>, то последовательность совпадает с числами Каталана. | |
===Аналитическая формула=== | ===Аналитическая формула=== | ||
| − | <tex dpi = 150> C_n = \ | + | <tex dpi = 150> C_n = \dfrac{1}{n+1} \dbinom {2n} {n} </tex> |
====Доказательство==== | ====Доказательство==== | ||
| − | Правильной скобочной структуре из <tex dpi = 120>n</tex> открывающих и <tex dpi = 120>n</tex> закрывающих скобок мы поставим в соответствие путь в квадрате <tex dpi = 120>[0, n]×[0, n]</tex>. Путь начинается в точке <tex dpi = 120>(0,0)</tex> и заканчивается в точке <tex dpi = 120>(n, n)</tex>. Открывающей скобке мы сопоставляем горизонтальный отрезок длины 1, а закрывающей — вертикальный. | + | Правильной скобочной структуре из <tex dpi = 120>n</tex> открывающих и <tex dpi = 120>n</tex> закрывающих скобок мы поставим в соответствие путь в квадрате <tex dpi = 120>[0, n]×[0, n]</tex>. Путь начинается в точке <tex dpi = 120>(0,0)</tex> и заканчивается в точке <tex dpi = 120>(n, n)</tex>. Открывающей скобке мы сопоставляем горизонтальный отрезок длины <tex dpi = 120>1</tex>, а закрывающей — вертикальный. |
Если путь сопоставлен правильной структуре, то ни одна его точка не может лежать выше главной диагонали квадрата. Обратно, такому пути ("правильному пути") сопоставляется правильная скобочная структура. | Если путь сопоставлен правильной структуре, то ни одна его точка не может лежать выше главной диагонали квадрата. Обратно, такому пути ("правильному пути") сопоставляется правильная скобочная структура. | ||
Геометрическое представление правильных скобочных структур позволяет найти выражение для чисел Каталана. | Геометрическое представление правильных скобочных структур позволяет найти выражение для чисел Каталана. | ||
| − | Сместим правильный путь на | + | Сместим правильный путь на одну клетку вниз. Теперь правильный путь начинается в точке |
| − | <tex dpi = 120> (0, -1) </tex>, заканчивается в точке <tex dpi = 120> (n, n-1) </tex> и не имеет общих точек с прямой <tex dpi = 120> y = x </tex> — биссектрисой первого квадранта. Нам нужно найти количество правильных путей. Для этого мы найдем количество неправильных, и из общего числа путей вычтем количество неправильных. Мы рассматриваем пути из точки <tex fpi = 120> (0, -1) </tex> в точку <tex dpi = 120> (n, n-1) </tex>. Длина такого пути равна <tex dpi = 120>2n</tex> и он содержит <tex dpi = 120>n</tex> вертикальных сегментов и <tex dpi = 120>n</tex> горизонтальных. Количество всех таких путей равно числу способов выбрать <tex dpi = 120>n</tex> вертикальных сегментов из общего числа <tex dpi = 120>2n</tex> сегментов, т.е. равно <tex dpi = 135> \ | + | <tex dpi = 120> (0, -1) </tex>, заканчивается в точке <tex dpi = 120> (n, n-1) </tex> и не имеет общих точек с прямой <tex dpi = 120> y = x </tex> — биссектрисой первого квадранта. Нам нужно найти количество правильных путей. Для этого мы найдем количество неправильных, и из общего числа путей вычтем количество неправильных. Мы рассматриваем пути из точки <tex fpi = 120> (0, -1) </tex> в точку <tex dpi = 120> (n, n-1) </tex>. Длина такого пути равна <tex dpi = 120>2n</tex> и он содержит <tex dpi = 120>n</tex> вертикальных сегментов и <tex dpi = 120>n</tex> горизонтальных. Количество всех таких путей равно числу способов выбрать <tex dpi = 120>n</tex> вертикальных сегментов из общего числа <tex dpi = 120>2n</tex> сегментов, т.е. равно <tex dpi = 135> \dbinom {2n}{n} </tex>. |
| − | Рассмотрим неправильный путь и его первую точку на прямой <tex dpi = 120> y = x </tex> (точка A). Отрезок пути от точки <tex dpi = 120>(0, -1)</tex> до точки A заменим симметричным относительно прямой <tex dpi = 120>y = x</tex>. Мы получим путь длины <tex dpi = 120>2n</tex>, идущий из точки <tex dpi = 120>( | + | Рассмотрим неправильный путь и его первую точку на прямой <tex dpi = 120> y = x </tex> (точка <tex dpi = 120>A</tex>). Отрезок пути от точки <tex dpi = 120>(0, -1)</tex> до точки <tex dpi = 120>A</tex> заменим симметричным относительно прямой <tex dpi = 120>y = x</tex>. Мы получим путь длины <tex dpi = 120>2n</tex>, идущий из точки <tex dpi = 120>(-1, 0)</tex> в точку <tex dpi = 120>(n, n-1)</tex> (Смотри рис.). |
[[Файл:Каталан2.PNG|right]] | [[Файл:Каталан2.PNG|right]] | ||
| − | Такой путь обязательно пересекает прямую <tex dpi = 120> y = x </tex>. Обратно, пусть нам дан путь длины <tex dpi = 120> 2n </tex> из точки <tex dpi = 120>(-1, 0)</tex> в точку <tex dpi = 120>(n, n-1)</tex> и пусть A — первая точка этого пути, лежащая на прямой <tex dpi = 120>y = x</tex>. Заменив участок пути от точки <tex dpi = 120>( | + | Такой путь обязательно пересекает прямую <tex dpi = 120> y = x </tex>. Обратно, пусть нам дан путь длины <tex dpi = 120> 2n </tex> из точки <tex dpi = 120>(-1, 0)</tex> в точку <tex dpi = 120>(n, n-1)</tex> и пусть <tex dpi = 120> A </tex> — первая точка этого пути, лежащая на прямой <tex dpi = 120>y = x</tex>. Заменив участок пути от точки <tex dpi = 120>(-1, 0)</tex> до точки <tex dpi = 120>A</tex> на симметричный относительно прямой <tex dpi = 120>y = x</tex>, мы получим неправильный путь из точки <tex dpi = 120>(0, -1)</tex> в точку <tex dpi = 120>(n, n-1)</tex>. Следовательно, неправильных путей из точки <tex dpi = 120>(0, -1)</tex> в точку <tex dpi = 120>(n, n-1)</tex> столько же, сколько путей из точки <tex dpi = 120>(-1, 0)</tex> в |
| − | точку <tex dpi = 120>(n, n-1)</tex>. Такой путь длины содержит <tex dpi = 120>n+1</tex> горизонтальных и <tex dpi = 120>n-1</tex> вертикальных участков. Поэтому, количество таких путей равно <tex dpi = 135> \ | + | точку <tex dpi = 120>(n, n-1)</tex>. Такой путь длины <tex dpi = 120>2n</tex> содержит <tex dpi = 120>n+1</tex> горизонтальных и <tex dpi = 120>n-1</tex> вертикальных участков. Поэтому, количество таких путей равно <tex dpi = 135> \dbinom {2n}{n-1} </tex>. Значит, количество правильных путей (т.е. число Каталана <tex dpi = 120>C_n</tex>) равно |
| − | <tex | + | <tex> C_n = \dbinom {2n} {n} - \dbinom {2n} {n-1} = \dfrac{2n!}{n!n!} - \dfrac{2n!}{(n-1)!(n+1)!} = \dfrac{2n!}{n!} (\dfrac{1}{n!} - \dfrac{1}{(n-1)! (n+1)}) = \dfrac{2n!}{n!n!(n+1)} = \dfrac{1}{n+1} \dbinom {2n} {n} </tex> |
| − | == | + | ==Задача разбиения выпуклого <tex dpi = 155 > n </tex>—угольника на треугольники не пересекающимися диагоналями== |
| − | === | + | ===Доказательство=== |
| + | [[Файл:Vectorpaint.png|145px|right]] | ||
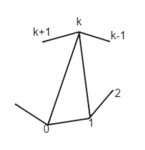
| − | [[Файл:Каталан.PNG| | + | Пусть <tex dpi = 120>t_n</tex> — число триангуляций выпуклого <tex dpi = 120> (n + 2) </tex>-угольника при <tex dpi = 120> n \geqslant 1 </tex>. Положим <tex dpi = 120> t_0 = 1 </tex>. Пронумеруем вершины многоугольника, начиная с произвольной против часовой стрелки. Рассмотрим произвольную триангуляцию и выделим треугольник, примыкающий к стороне <tex dpi = 120>01</tex> (см. рис.). |
| + | |||
| + | Пусть <tex dpi = 120>k</tex> — номер третьей вершины этого треугольника. Выделенный треугольник разбивает <tex dpi = 120>(n + 2)</tex> — угольник на <tex dpi = 120>k</tex> — угольник и <tex dpi = 120>(n-k+3)</tex> — угольник, каждый из которых триангулирован диагоналями. Перенумеруем вершины этих многоугольников против часовой стрелки так, чтобы нумерация вершин в каждом из них начиналась с 0. В результате получим пару триангуляций <tex dpi = 120>k</tex>-угольника и <tex dpi = 120>(n-k+3)</tex> — угольника. Наоборот, каждая пара триангуляций <tex dpi = 120>k</tex> — угольника и <tex dpi = 120>(n-k+3)</tex> — угольника | ||
| + | определяет триангуляцию исходного многоугольника. Поэтому | ||
| + | <tex dpi = 120>t_{n+1} = t_0 t_n + t_1 t_{n-1} + \ldots + t_n t_0 </tex> | ||
| + | и поскольку <tex dpi = 120>t_0 = 1</tex>, последовательность чисел <tex dpi = 120>t_n</tex> совпадает с последовательностью Каталана. | ||
| + | |||
| + | ===Пример=== | ||
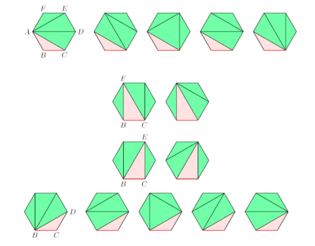
| + | [[Файл:Каталан.PNG|315px|thumb|right|Разбиение выпуклого шестиугольника]] | ||
Ответ на задачу при <tex dpi = 120> n = 3 </tex> тривиален: никаких | Ответ на задачу при <tex dpi = 120> n = 3 </tex> тривиален: никаких | ||
диагоналей проводить не надо. В четырёхугольнике можно провести любую из | диагоналей проводить не надо. В четырёхугольнике можно провести любую из | ||
| Строка 53: | Строка 68: | ||
к ней примыкают соответственно треугольники <tex dpi = 120> BCA, BCF, BCE </tex> и <tex dpi = 120> BCD </tex>. | к ней примыкают соответственно треугольники <tex dpi = 120> BCA, BCF, BCE </tex> и <tex dpi = 120> BCD </tex>. | ||
| − | Для семиугольника можно выделить одну из сторон и расклассифицировать разрезания в зависимости от того, какой треугольник к этой стороне примыкает. Имеем 5 разных случаев. В первом и последнем из них количество разбиений равно 14, | + | Для семиугольника можно выделить одну из сторон и расклассифицировать разрезания в зависимости от того, какой треугольник к этой стороне примыкает. Имеем <tex>5</tex> разных случаев. В первом и последнем из них количество разбиений равно <tex>14</tex>, |
ибо после отрезания треугольника остаётся шестиугольник. Во втором и четвёртом | ибо после отрезания треугольника остаётся шестиугольник. Во втором и четвёртом | ||
случаях при вырезании треугольника семиугольник распадается на треугольник и | случаях при вырезании треугольника семиугольник распадается на треугольник и | ||
| Строка 64: | Строка 79: | ||
способа.Такие вычисления можно проводить и дальше. | способа.Такие вычисления можно проводить и дальше. | ||
| − | == | + | ==Подсчет чисел Каталана== |
| − | + | Числа Каталана просто посчитать с помощью рекуррентной формулы. Для этого понадобится <tex dpi = 120>O(n)</tex> памяти и <tex dpi = 120>O(n^2)</tex> времени. За <tex dpi = 120>O(n)</tex> времени их можно посчитать, если использовать аналитическую формулу. Также из аналитической формулы можно выразить простую реккурентную формулу: | |
| + | |||
| + | <tex dpi = 135> C_n = \dfrac{4n-2}{n+1} C_{n-1} </tex>. | ||
| + | |||
| + | ==Вычисление [[Производящая функция |производящей функции]] чисел Каталана== | ||
| + | |||
| + | {{Лемма | ||
| + | |id=lemma1. | ||
| + | |statement=<tex>\dbinom{\frac{1}{2}}{k} = \dfrac{(-1)^{k - 1}}{(2k - 1) \cdot 4^k} \cdot \dbinom{2k}{k} </tex> | ||
| + | |proof= | ||
| + | <tex>\dbinom{\frac{1}{2}}{k} = \dfrac{\dfrac{1}{2} \cdot (\dfrac{1}{2} - 1) \cdot (\dfrac{1}{2} - 2) \cdots (\dfrac{1}{2} - k + 1)}{k!} = | ||
| + | \dfrac{1 \cdot (1 - 2) \cdot (1 - 4) \cdots (1 - 2k + 2)}{2^k \cdot k!} = \dfrac{1 \cdot (-1) \cdot (-3) \cdots (-2k + 3)}{2^k \cdot k!}</tex> | ||
| + | |||
| + | <tex> = \dfrac{(-1)^{k - 1}}{2k - 1} \cdot \dfrac{1 \cdot 3 \cdot (2k - 3) \cdot (2k - 1)}{2^k \cdot k!} = \dfrac{(-1)^{k - 1}}{2k - 1} \cdot \dfrac{1 \cdot 2 \cdot 3 \cdots (2k - 3) \cdot (2k - 2) \cdot (2k - 1) \cdot 2k}{2 \cdot 4 \cdots (2k - 2) \cdot 2k \cdot 2^k \cdot k!}</tex> | ||
| + | |||
| + | <tex>= \dfrac{(-1)^{k - 1}}{2k - 1} \cdot \dfrac{(2k)!}{(2 \cdot 1) \cdot (2 \cdot 2) \cdots (2 \cdot (2k - 1)) \cdot (2 \cdot k) \cdot 2^k \cdot k!} = \dfrac{(-1)^{k - 1}}{2k - 1} \cdot \dfrac{(2k)!}{2^k \cdot (1 \cdot 2 \cdots (k - 1) \cdot k) \cdot 2^k\cdot k!} </tex> | ||
| + | |||
| + | <tex> = \dfrac{(-1)^{k - 1}}{2k - 1} \cdot \dfrac{(2k)!}{2^k \cdot k! \cdot 2^k\cdot k!} = \dfrac{(-1)^{k - 1}}{(2k - 1) \cdot 2^k \cdot 2^k} \cdot \dfrac{(2k)!}{k! \cdot k!}= \dfrac{(-1)^{k - 1}}{(2k - 1) \cdot 4^k} \dbinom{2k}{k}</tex> | ||
| + | }} | ||
| + | |||
| + | {{Задача | ||
| + | |definition = Вычислить производящую функцию чисел Каталана | ||
| + | }} | ||
| + | |||
| + | Пусть мы имеем последовательность чисел Каталана <tex>(C_0, C_1, C_2, \ldots)</tex>. | ||
| + | |||
| + | Будем искать её производящую функцию в виде <tex>G(z) = \sum\limits_{n = 0}^{\infty} C_n \cdot z^n</tex> | ||
| + | |||
| + | Как известно, рекуррентное соотношение для чисел Каталана имеет вид | ||
| + | |||
| + | <tex> | ||
| + | |||
| + | C_n= | ||
| + | \begin{cases} | ||
| + | 1,&\text{если $n = 0$;}\\ | ||
| + | \sum\limits_{k = 0}^{n - 1}C_k C_{n - k - 1},&\text{если $n > 0$.} | ||
| + | \end{cases} | ||
| + | |||
| + | </tex> | ||
| + | |||
| + | Домножаем <tex>C_n</tex> на <tex>z^n</tex>, получая | ||
| + | |||
| + | <tex> | ||
| + | |||
| + | z^n \cdot C_n= | ||
| + | \begin{cases} | ||
| + | z^0 = 1,&\text{если $n = 0$;}\\ | ||
| + | z^n \sum\limits_{k = 0}^{n - 1}C_k C_{n - k - 1},&\text{если $n > 0$.} | ||
| + | \end{cases} | ||
| + | |||
| + | </tex> | ||
| + | |||
| + | Суммируя <tex>C_n z^n</tex> по всем <tex>n</tex> от <tex>0</tex> до <tex>\infty</tex>, получаем: | ||
| + | |||
| + | <tex>G(z) = \sum\limits_{n = 0}^{\infty} C_n z^n = C_0 z^0 + \sum\limits_{n = 1}^{\infty}z^n \sum\limits_{k = 0}^{n - 1} C_k C_{n - k - 1} = | ||
| + | C_0 + \sum\limits_{n = 1}^{\infty}z^n \sum\limits_{k = 0}^{n - 1} C_k C_{n - k - 1} = 1 + \sum\limits_{n = 1}^{\infty}z^n \sum\limits_{k = 0}^{n - 1} C_k C_{n - k - 1}</tex> (так как <tex>C_0 = 1</tex> по определению чисел Каталана). | ||
| + | |||
| + | Получили, что <tex>G(z) = 1 + \sum\limits_{n = 1}^{\infty}z^n \sum\limits_{k = 0}^{n - 1} C_k C_{n - k - 1}~~~~~ \textbf{(1)}</tex> | ||
| + | |||
| + | Распишем произведение <tex>G(z) \cdot G(z)</tex> по определению [[Арифметические действия с формальными степенными рядами#def_mul | произведения формальных степенных рядов]]. | ||
| + | |||
| + | <tex>G(z) \cdot G(z) = (\sum\limits_{n = 0}^{\infty} C_n z^n) \cdot (\sum\limits_{n = 0}^{\infty} C_n z^n) = \sum\limits_{n = 0}^{\infty}z^n \sum\limits_{k = 0}^{n} C_k C_{n - k}</tex> | ||
| + | |||
| + | В последнем выражении выполним сдвиг индексации, положив <tex>n' = n + 1</tex>. Тогда имеем: <tex>n = n' - 1, n = 0 \Rightarrow n' = 1</tex>. Кроме того, <tex>z^n = z^{n' - 1}</tex>. <tex>n - k</tex> преобразуется в <tex>n' - 1 - k</tex> (так как <tex>n' - 1 = n</tex>). Тогда, преобразуя предыдущее выражение, получаем: | ||
| + | |||
| + | <tex>G(z) \cdot G(z) = \sum\limits_{n = 0}^{\infty}z^n \sum\limits_{k = 0}^{n} C_k C_{n - k} = \sum\limits_{n' = 1}^{\infty}z^{n' - 1} \sum\limits_{k = 0}^{n' - 1} C_k C_{n' - k - 1}</tex> | ||
| + | |||
| + | Домножая это произведение на <tex>z</tex>, получаем | ||
| + | |||
| + | <tex>z \cdot G^2(z) = z \cdot \sum\limits_{n' = 1}^{\infty}z^{n' - 1} \sum\limits_{k = 0}^{n' - 1} C_k C_{n' - k - 1} = \sum\limits_{n' = 1}^{\infty}z^{n'} \sum\limits_{k = 0}^{n' - 1} C_k C_{n' - k - 1}</tex> | ||
| + | |||
| + | Тогда | ||
| + | |||
| + | <tex>z \cdot G^2(z) = \sum\limits_{n = 1}^{\infty}z^{n} \sum\limits_{k = 0}^{n - 1} C_k C_{n - k - 1} ~~~~ \textbf{(2)}</tex> | ||
| + | |||
| + | Из <tex> \textbf{(1)}</tex> и <tex>\textbf{(2)}</tex> получаем: | ||
| + | |||
| + | <tex>G(z) = 1 + z \cdot G^2(z)</tex> | ||
| + | |||
| + | Преобразуя, получаем квадратное уравнение на <tex>G(z) :</tex> | ||
| + | |||
| + | <tex>z \cdot G^2(z) - G(z) + 1 = 0</tex> | ||
| + | |||
| + | Из этого квадратного уравнения находим два варианта <tex>G(z) :</tex> | ||
| + | |||
| + | <tex>G(z) = \dfrac{1 \pm \sqrt{1-4z}}{2z}</tex> | ||
| + | |||
| + | Выберем из двух корней тот, который удовлетворяет определению <tex>G(z)</tex> как производящей функции чисел Каталана. | ||
| + | |||
| + | Домножая обе части на <tex>2z</tex>, получаем <tex>G(z) \cdot 2z = 1 \pm \sqrt{1-4z} ~~~~~\textbf{(3)}</tex> | ||
| + | |||
| + | Выберем нужный из двух корней, посчитав значение обеих частей при <tex>z = 0</tex> | ||
| + | |||
| + | Из определения производящей функции для чисел Каталана известно, что <tex>G(z) = C_0 + C_1 \cdot x + \ldots + C_n \cdot x^n + \ldots</tex>, тогда <tex>G(0) = C_0 = 1</tex> | ||
| + | |||
| + | Тогда при <tex>z = 0</tex> выражение <tex>\textbf{(3)}</tex> принимает вид <tex>G(0) \cdot 2 \cdot 0 = 1 \pm \sqrt{1-4 \cdot 0}</tex>, или <tex>0 = 1 \pm 1</tex>. | ||
| + | |||
| + | Тогда очевидно, нужно выбрать знак <tex>-</tex> в выражении, чтобы при <tex>z = 0</tex> левая и правая части были равны. | ||
| + | |||
| + | Тогда <tex>G(z) = \dfrac{1 - \sqrt{1-4z}}{2z}</tex> | ||
| + | |||
| + | Проверим, что <tex>G(z)</tex> действительно является производящей функцией чисел Каталана. Для этого разложим <tex>G(z)</tex> в ряд. | ||
| − | + | <tex>G(z) = \dfrac{1 - \sqrt{1-4z}}{2z} = \dfrac{1}{2z} - \dfrac{\sqrt{1-4z}}{2z} = \dfrac{1}{2z} - \dfrac{1}{2z} \cdot \sqrt{1 - 4z} = \dfrac{1}{2z} - \dfrac{1}{2z} \cdot (1 - 4z)^{\frac{1}{2}} = \dfrac{1}{2z} - \dfrac{1}{2z} \cdot \sum\limits_{n = 0}^{\infty} ((-4z)^n \cdot \dbinom{\frac{1}{2}}{n})</tex> | |
| − | + | <tex> = \dfrac{1}{2z} - \dfrac{1}{2z} \cdot \sum\limits_{n = 0}^{\infty} ((-4z)^n \cdot \dfrac{(-1)^{n - 1}}{(2n - 1) \cdot 4^n} \cdot \dbinom{2n}{n}) = \dfrac{1}{2z} - \dfrac{1}{2z} \cdot \sum\limits_{n = 0}^{\infty} (\dfrac{(-1)^n \cdot 4^n \cdot z^n \cdot (-1)^{n - 1}}{(2n - 1) \cdot 4^n} \cdot \dbinom{2n}{n}) = \dfrac{1}{2z} - \dfrac{1}{2z} \cdot \sum\limits_{n = 0}^{\infty} (\dfrac{(-1)^{2n - 1} \cdot 4^n \cdot z^n}{(2n - 1) \cdot 4^n} \cdot \dbinom{2n}{n})</tex> | |
| − | |||
| − | |||
| − | |||
| − | === | + | <tex> = \dfrac{1}{2z} - \dfrac{1}{2z} \cdot \sum\limits_{n = 0}^{\infty} (\dfrac{-z^n}{(2n - 1)} \cdot \dbinom{2n}{n}) = \dfrac{1}{2z} - \dfrac{1}{2z} \cdot \dfrac{-z^0}{2 \cdot 0 - 1} \cdot \dbinom{2 \cdot 0}{0} - \dfrac{1}{2z} \cdot \sum\limits_{n = 1}^{\infty} (\dfrac{-z^n}{(2n - 1)} \cdot \dbinom{2n}{n})</tex> |
| − | + | <tex>= \dfrac{1}{2z} - \dfrac{1}{2z} \cdot \dfrac{-1}{-1} \cdot 1- \dfrac{1}{2z} \cdot \sum\limits_{n = 1}^{\infty} (\dfrac{-z^n}{(2n - 1)} \cdot \dbinom{2n}{n}) = \dfrac{1}{2z} - \dfrac{1}{2z} - \dfrac{1}{2z} \cdot \sum\limits_{n = 1}^{\infty} (\dfrac{-z^n}{(2n - 1)} \cdot \dbinom{2n}{n}) = \dfrac{1}{2z} \cdot \sum\limits_{n = 1}^{\infty} (\dfrac{z^n}{(2n - 1)} \cdot \dbinom{2n}{n})</tex> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <tex> = \sum\limits_{n = 1}^{\infty} (\dfrac{z^{n - 1}}{(4n - 2)} \cdot \dbinom{2n}{n}) = \sum\limits_{n = 0}^{\infty} (\dfrac{z^{n}}{(4n + 2)} \cdot \dbinom{2n + 2}{n + 1}) = \sum\limits_{n = 0}^{\infty} (\dfrac{z^{n}}{(4n + 2)} \cdot \dbinom{2n + 2}{n + 1}) = \sum\limits_{n = 0}^{\infty} (\dfrac{z^{n}}{(4n + 2)} \cdot \dfrac{(2n + 2)!}{(n + 1)! \cdot (n + 1)!}</tex> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <tex> = \sum\limits_{n = 0}^{\infty} (\dfrac{z^{n}}{(4n + 2)} \cdot \dfrac{(2n)! \cdot (2n + 1) \cdot 2 \cdot (n + 1)}{(n)! \cdot (n)! \cdot (n + 1) \cdot (n + 1)}) = \sum\limits_{n = 0}^{\infty} (\dfrac{z^{n}}{(4n + 2)} \cdot \dfrac{2 \cdot (2n + 1)}{n + 1} \cdot \dbinom{2n}{n}) = \sum\limits_{n = 0}^{\infty} (\dfrac{z^{n}}{(4n + 2)} \cdot \dfrac{(4n + 2)}{n + 1} \cdot \dbinom{2n}{n})</tex> | |
| − | |||
| − | + | <tex>= \sum\limits_{n = 0}^{\infty} (\dfrac{z^{n}}{(4n + 2)} \cdot \dfrac{2 \cdot (2n + 1)}{n + 1} \cdot \dbinom{2n}{n}) = \sum\limits_{n = 0}^{\infty} (z^n \cdot \dfrac{1}{n + 1} \cdot \dbinom{2n}{n})</tex> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Тогда коэффициент при <tex>z^n</tex> в разложении <tex>G(z)</tex> равен <tex>\dfrac{1}{n + 1} \cdot \dbinom{2n}{n}</tex>, что совпадает с аналитической формулой для чисел Каталана. (<tex>C_n = \dfrac{1}{n + 1} \cdot \dbinom{2n}{n}</tex>) Поэтому <tex>G(z) = \sum\limits_{n = 0}^{\infty} z^n \cdot C_n</tex>, поэтому <tex>G(z) = \dfrac{1 - \sqrt{1-4z}}{2z}</tex> является производящей функцией чисел Каталана. | |
| − | |||
| − | { | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Смотри также== | ==Смотри также== | ||
| − | + | *[[Производящая_функция|Производящая функция]] | |
| − | *[ | + | |
| − | *[ | + | *[[Числа_Стирлинга_первого_рода|Числа Стирлинга первого рода]] |
| − | + | ||
| − | ==Источники== | + | *[[Числа_Стирлинга_второго_рода|Числа Стирлинга второго рода]] |
| − | + | ||
| + | *[[Числа_Эйлера_I_и_II_рода|Числа Эйлера первого и второго рода]] | ||
| + | |||
| + | ==Источники информации== | ||
*[http://e-maxx.ru/algo/catalan_numbers MAXimal :: algo :: Числа Каталана] | *[http://e-maxx.ru/algo/catalan_numbers MAXimal :: algo :: Числа Каталана] | ||
| + | |||
*[http://habrahabr.ru/post/165295/ Числа Каталана / Хабрахабр] | *[http://habrahabr.ru/post/165295/ Числа Каталана / Хабрахабр] | ||
| − | *[https://ru.wikipedia.org/wiki/%D0%A7%D0%B8%D1%81%D0%BB%D0%B0_%D0%9A%D0%B0%D1%82%D0%B0%D0%BB%D0%B0%D0%BD%D0%B0 Числа Каталана | + | |
| + | *[https://ru.wikipedia.org/wiki/%D0%A7%D0%B8%D1%81%D0%BB%D0%B0_%D0%9A%D0%B0%D1%82%D0%B0%D0%BB%D0%B0%D0%BD%D0%B0 Википедия — Числа Каталана] | ||
| + | |||
*[http://kvant.mccme.ru/1978/07/chisla_katalana.htm Журнал "Квант"] | *[http://kvant.mccme.ru/1978/07/chisla_katalana.htm Журнал "Квант"] | ||
| + | |||
*[http://desolt.ru/karimova.html Глава 5. Комбинаторика] | *[http://desolt.ru/karimova.html Глава 5. Комбинаторика] | ||
| − | |||
| − | |||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Комбинаторика ]] | [[Категория: Комбинаторика ]] | ||
Текущая версия на 19:37, 4 сентября 2022
Содержание
Числа Каталана
| Определение: |
Числа Каталана — последовательность чисел, выражающих:
|
Первые несколько чисел Каталана:
Формулы вычисления чисел Каталана
Рекуррентная формула
Доказательство
Рекуррентную формулу легко вывести из задачи о правильных скобочных последовательностях.
Пусть — произвольная правильная скобочная последовательность длины . Она начинается с открывающейся скобки. Найдем парную ей закрывающуюся скобку и представим последовательность в виде: , где и — тоже правильные скобочные последовательности. Если длина последовательности равна , то последовательность можно составить способами. Тогда длина последовательности равна и последовательность можно составить способами. Комбинация любого способа составить последовательность с любым способом составить последовательность даст новую последовательность , а величина может меняться от до . Получили рекуррентное соотношение: . Так как , то последовательность совпадает с числами Каталана.
Аналитическая формула
Доказательство
Правильной скобочной структуре из открывающих и закрывающих скобок мы поставим в соответствие путь в квадрате . Путь начинается в точке и заканчивается в точке . Открывающей скобке мы сопоставляем горизонтальный отрезок длины , а закрывающей — вертикальный. Если путь сопоставлен правильной структуре, то ни одна его точка не может лежать выше главной диагонали квадрата. Обратно, такому пути ("правильному пути") сопоставляется правильная скобочная структура. Геометрическое представление правильных скобочных структур позволяет найти выражение для чисел Каталана.
Сместим правильный путь на одну клетку вниз. Теперь правильный путь начинается в точке , заканчивается в точке и не имеет общих точек с прямой — биссектрисой первого квадранта. Нам нужно найти количество правильных путей. Для этого мы найдем количество неправильных, и из общего числа путей вычтем количество неправильных. Мы рассматриваем пути из точки в точку . Длина такого пути равна и он содержит вертикальных сегментов и горизонтальных. Количество всех таких путей равно числу способов выбрать вертикальных сегментов из общего числа сегментов, т.е. равно .
Рассмотрим неправильный путь и его первую точку на прямой (точка ). Отрезок пути от точки до точки заменим симметричным относительно прямой . Мы получим путь длины , идущий из точки в точку (Смотри рис.).
Такой путь обязательно пересекает прямую . Обратно, пусть нам дан путь длины из точки в точку и пусть — первая точка этого пути, лежащая на прямой . Заменив участок пути от точки до точки на симметричный относительно прямой , мы получим неправильный путь из точки в точку . Следовательно, неправильных путей из точки в точку столько же, сколько путей из точки в точку . Такой путь длины содержит горизонтальных и вертикальных участков. Поэтому, количество таких путей равно . Значит, количество правильных путей (т.е. число Каталана ) равно
Задача разбиения выпуклого —угольника на треугольники не пересекающимися диагоналями
Доказательство
Пусть — число триангуляций выпуклого -угольника при . Положим . Пронумеруем вершины многоугольника, начиная с произвольной против часовой стрелки. Рассмотрим произвольную триангуляцию и выделим треугольник, примыкающий к стороне (см. рис.).
Пусть — номер третьей вершины этого треугольника. Выделенный треугольник разбивает — угольник на — угольник и — угольник, каждый из которых триангулирован диагоналями. Перенумеруем вершины этих многоугольников против часовой стрелки так, чтобы нумерация вершин в каждом из них начиналась с 0. В результате получим пару триангуляций -угольника и — угольника. Наоборот, каждая пара триангуляций — угольника и — угольника определяет триангуляцию исходного многоугольника. Поэтому и поскольку , последовательность чисел совпадает с последовательностью Каталана.
Пример
Ответ на задачу при тривиален: никаких диагоналей проводить не надо. В четырёхугольнике можно провести любую из двух диагоналей, так что способов два. В пятиугольнике — из любой вершины две диагонали, способов. При — первый не вполне очевидный ответ: способов (см. рис.); чтобы не запутаться, сторона BC выделена и отдельно нарисованы разрезания, в которых к ней примыкают соответственно треугольники и .
Для семиугольника можно выделить одну из сторон и расклассифицировать разрезания в зависимости от того, какой треугольник к этой стороне примыкает. Имеем разных случаев. В первом и последнем из них количество разбиений равно , ибо после отрезания треугольника остаётся шестиугольник. Во втором и четвёртом случаях при вырезании треугольника семиугольник распадается на треугольник и пятиугольник. В третьем случае семиугольник распадается на два четырёхугольника. Поскольку каждый из них можно разбить двумя способами, получаем варианта. Итак, семиугольник можно разбить всего способами. Рассматривая восьмиугольник, аналогично получаем способа.Такие вычисления можно проводить и дальше.
Подсчет чисел Каталана
Числа Каталана просто посчитать с помощью рекуррентной формулы. Для этого понадобится памяти и времени. За времени их можно посчитать, если использовать аналитическую формулу. Также из аналитической формулы можно выразить простую реккурентную формулу:
.
Вычисление производящей функции чисел Каталана
| Лемма: |
| Доказательство: |
|
|
| Задача: |
| Вычислить производящую функцию чисел Каталана |
Пусть мы имеем последовательность чисел Каталана .
Будем искать её производящую функцию в виде
Как известно, рекуррентное соотношение для чисел Каталана имеет вид
Домножаем на , получая
Суммируя по всем от до , получаем:
(так как по определению чисел Каталана).
Получили, что
Распишем произведение по определению произведения формальных степенных рядов.
В последнем выражении выполним сдвиг индексации, положив . Тогда имеем: . Кроме того, . преобразуется в (так как ). Тогда, преобразуя предыдущее выражение, получаем:
Домножая это произведение на , получаем
Тогда
Из и получаем:
Преобразуя, получаем квадратное уравнение на
Из этого квадратного уравнения находим два варианта
Выберем из двух корней тот, который удовлетворяет определению как производящей функции чисел Каталана.
Домножая обе части на , получаем
Выберем нужный из двух корней, посчитав значение обеих частей при
Из определения производящей функции для чисел Каталана известно, что , тогда
Тогда при выражение принимает вид , или .
Тогда очевидно, нужно выбрать знак в выражении, чтобы при левая и правая части были равны.
Тогда
Проверим, что действительно является производящей функцией чисел Каталана. Для этого разложим в ряд.
Тогда коэффициент при в разложении равен , что совпадает с аналитической формулой для чисел Каталана. () Поэтому , поэтому является производящей функцией чисел Каталана.