Двумерная разреженная таблица — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 20 промежуточных версий 11 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''2D Sparse Table'' | + | '''Двумерная разреженная таблица''' (англ. ''2D Sparse Table'') {{---}} структура данных, которая позволяет решать задачу online static RMQ. |
{{Задача | {{Задача | ||
| − | |definition = Дан двумерный массив <tex>A[1 \ldots N][1 \ldots M]</tex> целых чисел. Поступают запросы вида <tex>(x_1, y_1, x_2, y_2)</tex> такие, что <tex> x_1 | + | |definition = Дан двумерный массив <tex>A[1 \ldots N][1 \ldots M]</tex> целых чисел. Поступают запросы вида <tex>(x_1, y_1, x_2, y_2)</tex> такие, что <tex> x_1 \leqslant x_2 </tex> и <tex> y_1 \leqslant y_2 </tex> , для каждого из которых требуется найти минимум среди <tex>A[i][j], x_1 \leqslant i \leqslant x_2 </tex> и <tex> y_1 \leqslant j \leqslant y_2 </tex>. |
}} | }} | ||
== Структура 2D Sparse Table == | == Структура 2D Sparse Table == | ||
| − | В целом структура 2D Sparse Table схожа со структурой обычной [[Решение_RMQ_с_помощью_разреженной_таблицы| | + | В целом структура 2D Sparse Table схожа со структурой обычной [[Решение_RMQ_с_помощью_разреженной_таблицы| разреженной таблицы]]. |
| − | + | Разреженная таблица представляет собой четырехмерный массив: | |
| − | + | <tex>ST[N][M][LOGN][LOGM]</tex>, где <tex>LOGN = \log(N), LOGM = \log(M)</tex>. | |
| − | + | ||
| − | + | <tex> ST[i][j][k_1][k_2] = \min\limits_{r = i,\dots,i+2^{k_1}-1, c = j,\ldots,j + 2^{k_2}-1} A[r][c], r < N, c < M </tex> | |
| + | |||
То есть в ячейке структуры мы храним минимум для подматрицы, длины сторон которого являются некоторыми степенями двойки. | То есть в ячейке структуры мы храним минимум для подматрицы, длины сторон которого являются некоторыми степенями двойки. | ||
| + | |||
| + | [[Файл:STP1.png|left]] | ||
| + | [[Файл:SparseTableExample1Picture.png|right]] | ||
| + | |||
| + | Рассмотрим иллюстрации. | ||
| + | |||
| + | Слева изображен общий случай. Пусть <tex>n + 1</tex> {{---}} количество строк, <tex>m + 1</tex> {{---}} количество столбцов массива A. Рассмотрим элемент на позиции <tex>(i, j)</tex>, который выделен желтым цветом. Данный элемент является левым верхним углом прямоугольника, стороны которого равны <tex>2^{k_1}</tex> и <tex>2^{k_2}</tex>. Прямоугольна выделен красным, а проекции его сторон - зеленым. Тогда в <tex>ST[i][j][k_1][k_2]</tex> будет храниться минимум из всех элементов, которые входят в красную и желтую область. | ||
| + | |||
| + | Справа изображен частный случай, когда N = 11, M = 11. Посмотрим, что будет храниться в <tex>ST[2][1][2][3]</tex>: | ||
| + | Клетка (2, 1), которая выделена желтым цветом, является левым верхним углом красного прямоугольника, длины сторон которого <tex>2^{2}</tex> и <tex>2^{3}</tex> (проекции этих сторон выделены зеленым цветом). И по определению выше, <tex>ST[2][1][3][2]</tex> хранит минимум из элементов красной области. | ||
== Реализация 2D Sparse Table == | == Реализация 2D Sparse Table == | ||
| − | + | ===Построение=== | |
| − | + | Изначально заполним таблицу следующим образом: | |
| − | + | $$ST[i][j][k_1][k_2]= | |
| − | + | \begin{cases} | |
| − | + | \infty ,&\text{если $k_1\neq0 \lor k_2\neq0$ ;}\\ | |
| − | + | A[i][j], &\text {если $k_1=0 \wedge k_2=0$ ;} | |
| + | \end{cases} | ||
| + | $$ | ||
| − | Далее мы считаем [[Решение_RMQ_с_помощью_разреженной_таблицы| | + | Далее мы считаем [[Решение_RMQ_с_помощью_разреженной_таблицы|одномерную разреженную таблицу]] для каждого столбца: |
| − | '''for''' | + | '''for''' <tex> i = 0 </tex> '''to''' <tex> N </tex> |
| − | '''for''' | + | '''for''' <tex> lg = 1 </tex> '''to''' <tex> \log(M) </tex> |
| − | + | '''for''' <tex> j = 0 </tex> '''to''' <tex> M </tex> | |
| − | + | <tex>ST[i][j][0][lg] = \min(ST[i][j][0][lg - 1], ST[i][j+ 2^{lg-1}][0][lg - 1])</tex> | |
| − | <tex>ST[i][j][0][lg] = min(ST[i][j][0][lg - 1], ST[i][j+ 2^{lg}][0][lg - 1]) | ||
| − | Следующим шагом мы можем обновить значения для подматриц, так как для всех | + | Следующим шагом мы можем обновить значения для подматриц, так как для всех столбцов ответы уже известны. Будем это делать по аналогичному алгоритму для 1D Sparse Table. |
| − | '''for''' <tex> k_1 </tex> | + | '''for''' <tex> k_1 = 1 </tex> '''to''' <tex> \log(N) </tex> |
| − | '''for''' <tex> | + | '''for''' <tex> i = 0 </tex> '''to''' <tex> N </tex> |
| − | '''for''' | + | '''for''' <tex> k_2 = 0 </tex> '''to''' <tex> \log(M) </tex> |
| − | '''for''' j | + | '''for''' <tex> j = 0 </tex> '''to''' <tex> M </tex> |
| − | + | <tex>ST[i][j][k_1][k_2]=\min\left(ST[i][j][k_1 - 1][k_2],ST[i+2^{k_1-1}][j][k_1 - 1][k_2]\right)</tex> | |
| − | |||
| − | Таким образом мы получили | + | Таким образом мы получили двумерную разреженную таблицу за <tex>O(NM\log(N)\log(M))</tex> |
| − | + | ===Ответы на запросы=== | |
| − | Для ответа на запрос | + | Для ответа на запрос <tex> \mathrm {RMQ(l, r)} </tex> в 1D Sparse Table использовалось пересечение отрезков <tex> [l, l + 2^{k}] </tex> и <tex> [r - 2^{k} + 1, r] </tex>, где <tex> k = \lfloor \log(SZ) \rfloor , SZ </tex> {{---}} размера массива для одномерной задачи. |
Тут мы будем пользоваться аналогичным утверждением для матриц. Таким образов минимум на подматрице <tex>(x_1, y_1, x_2, y_2)</tex> будет высчитываться следующим образом: | Тут мы будем пользоваться аналогичным утверждением для матриц. Таким образов минимум на подматрице <tex>(x_1, y_1, x_2, y_2)</tex> будет высчитываться следующим образом: | ||
| − | <tex> k_1 = \lfloor \log(x_2 - x_1 + 1) \rfloor | + | <tex> k_1 = \lfloor \log(x_2 - x_1 + 1) \rfloor </tex> |
| − | <tex> | + | <tex> k_2 = \lfloor \log(y_2 - y_1 + 1) \rfloor </tex> |
| − | + | <tex> ans_1 = ST[x_1][y_1][k_1][k_2] </tex> <span style="color:#008000"> // красный прямоугольник | |
| + | <tex> ans_2 = ST[x_2 - 2^{k_1} + 1][y_1][k_1][k_2] </tex> <span style="color:#008000"> // Y-прямоугольник | ||
| + | <tex> ans_3 = ST[x_1][y_2 - 2^{k_2} + 1][k_1][k_2] </tex> <span style="color:#008000"> // AA-прямоугольник | ||
| + | <tex> ans_4 = ST[x_2 - 2^{k_1} + 1][y_2 - 2^{k_2} + 1][k_1][k_2] </tex> <span style="color:#008000"> // белый прямоугольник | ||
| + | <tex> ans = \min\left(ans_1, ans_2, ans_3, ans_4\right) </tex> | ||
| + | |||
| + | [[Файл:ST3.png|center]] | ||
| + | |||
| + | Таким образом мы получаем ответ на запрос <tex> \mathrm {RMQ(x_1, y_1, x_2, y_2)} </tex> за <tex> O(1) </tex>, если предпосчитать логарифмы двоек, например так: | ||
| + | <tex> lg[1] = 0 </tex> | ||
| + | '''for''' <tex> i = 2 </tex> '''to''' <tex>\max\left(N, M\right)</tex> | ||
| + | <tex> lg[i] = lg[i / 2] + 1 </tex> | ||
| − | + | === Обобщение на большие размерности === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Можно заметить, что возможно реализовать и D-мерную разреженную таблицу за <tex>O((N\log(n))^{D})</tex> памяти и <tex>O((N\log(n))^{D})</tex> времени на построение, где ответ на запрос, например, <tex> \mathrm {RMQ(l, r)} </tex> будет выполняться за <tex> O(2^{D}) </tex>. | ||
| − | ---- | + | ''Способ построения'': Если в данном случае, для того, чтобы построить двумерную структуру мы сначала должны были построить одномерную, то также и в случае с D-мерной структуре - сначала нужно построить (D-1)-мерную, а из нее получить D-мерную. |
| − | + | ''Ответ на запрос'': Абсолютно аналогичен рассмотренному здесь, только обобщается до размерности D. | |
| − | == | + | == См. также == |
| − | [[Решение_RMQ_с_помощью_разреженной_таблицы| Решение RMQ с помощью разреженной таблицы]] | + | * [[Решение_RMQ_с_помощью_разреженной_таблицы| Решение RMQ с помощью разреженной таблицы]] |
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
| + | [[Категория: Задача о наименьшем общем предке]] | ||
Текущая версия на 19:37, 4 сентября 2022
Двумерная разреженная таблица (англ. 2D Sparse Table) — структура данных, которая позволяет решать задачу online static RMQ.
| Задача: |
| Дан двумерный массив целых чисел. Поступают запросы вида такие, что и , для каждого из которых требуется найти минимум среди и . |
Содержание
Структура 2D Sparse Table
В целом структура 2D Sparse Table схожа со структурой обычной разреженной таблицы.
Разреженная таблица представляет собой четырехмерный массив: , где .
То есть в ячейке структуры мы храним минимум для подматрицы, длины сторон которого являются некоторыми степенями двойки.
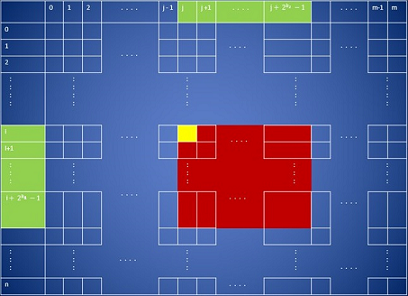
Рассмотрим иллюстрации.
Слева изображен общий случай. Пусть — количество строк, — количество столбцов массива A. Рассмотрим элемент на позиции , который выделен желтым цветом. Данный элемент является левым верхним углом прямоугольника, стороны которого равны и . Прямоугольна выделен красным, а проекции его сторон - зеленым. Тогда в будет храниться минимум из всех элементов, которые входят в красную и желтую область.
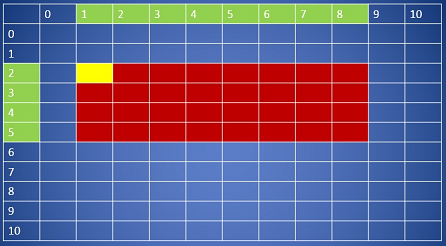
Справа изображен частный случай, когда N = 11, M = 11. Посмотрим, что будет храниться в : Клетка (2, 1), которая выделена желтым цветом, является левым верхним углом красного прямоугольника, длины сторон которого и (проекции этих сторон выделены зеленым цветом). И по определению выше, хранит минимум из элементов красной области.
Реализация 2D Sparse Table
Построение
Изначально заполним таблицу следующим образом:
$$ST[i][j][k_1][k_2]= \begin{cases} \infty ,&\text{если $k_1\neq0 \lor k_2\neq0$ ;}\\ A[i][j], &\text {если $k_1=0 \wedge k_2=0$ ;} \end{cases} $$
Далее мы считаем одномерную разреженную таблицу для каждого столбца:
for to for to for to
Следующим шагом мы можем обновить значения для подматриц, так как для всех столбцов ответы уже известны. Будем это делать по аналогичному алгоритму для 1D Sparse Table.
for to for to for to for to
Таким образом мы получили двумерную разреженную таблицу за
Ответы на запросы
Для ответа на запрос в 1D Sparse Table использовалось пересечение отрезков и , где — размера массива для одномерной задачи.
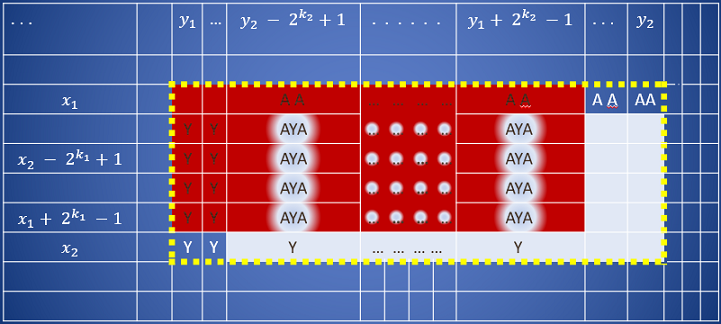
Тут мы будем пользоваться аналогичным утверждением для матриц. Таким образов минимум на подматрице будет высчитываться следующим образом:
// красный прямоугольник // Y-прямоугольник // AA-прямоугольник // белый прямоугольник
Таким образом мы получаем ответ на запрос за , если предпосчитать логарифмы двоек, например так:
for to
Обобщение на большие размерности
Можно заметить, что возможно реализовать и D-мерную разреженную таблицу за памяти и времени на построение, где ответ на запрос, например, будет выполняться за .
Способ построения: Если в данном случае, для того, чтобы построить двумерную структуру мы сначала должны были построить одномерную, то также и в случае с D-мерной структуре - сначала нужно построить (D-1)-мерную, а из нее получить D-мерную.
Ответ на запрос: Абсолютно аналогичен рассмотренному здесь, только обобщается до размерности D.
См. также