Формула Эйлера — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 18 промежуточных версий 9 участников) | |||
| Строка 1: | Строка 1: | ||
| + | ==Двумерный случай== | ||
{{Теорема | {{Теорема | ||
|about= | |about= | ||
| − | + | формула Эйлера | |
|statement= | |statement= | ||
| − | Для произвольного плоского связного графа <tex>G</tex> с <tex>V</tex> вершинами, <tex>E</tex> ребрами и <tex>F</tex> гранями справедливо следующее соотношение: | + | Для произвольного [[Укладка графа на плоскости|плоского]] связного графа <tex>G</tex> с <tex>V</tex> вершинами, <tex>E</tex> ребрами и <tex>F</tex> [[Укладка графа на плоскости|гранями]] справедливо следующее соотношение: |
<br/><tex>V - E + F = 2</tex> | <br/><tex>V - E + F = 2</tex> | ||
|proof= | |proof= | ||
| − | + | ||
| − | + | ||
Воспользуемся методом математической индукции по количеству граней графа. | Воспользуемся методом математической индукции по количеству граней графа. | ||
<br /> | <br /> | ||
| Строка 15: | Строка 16: | ||
'''Индукционный переход''': | '''Индукционный переход''': | ||
<br /> | <br /> | ||
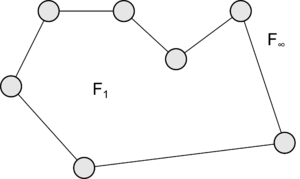
| − | Покажем, что если теорема верна для графов с <tex>F</tex> гранями, то она будет верна и для графов с <tex>F + 1</tex> гранями. Пусть <tex>G</tex> - плоский граф, имеющий <tex>V</tex> вершин, <tex>E</tex> ребер и <tex>F</tex> граней, и для него справедлива формула Эйлера. Добавим новую грань (пунктирная линия на рис.2), проводя по внешней грани <tex>F_{\infty}</tex> некоторую элементарную цепь, соединяющую две вершины максимального цикла графа <tex>G</tex>. Если эта цепь имеет <tex>r</tex> ребер, то необходимо добавить <tex>r - 1</tex> новых вершин и одну новую грань. Ясно, что формула Эйлера останется справедливой и для нового графа, так как <tex>V' - E' + F' = (V + r - 1) - (E + r) + (F + 1) = V - E + F</tex> | + | Покажем, что если теорема верна для графов с <tex>F</tex> гранями, то она будет верна и для графов с <tex>F + 1</tex> гранями. Пусть <tex>G</tex> {{---}} плоский граф, имеющий <tex>V</tex> вершин, <tex>E</tex> ребер и <tex>F</tex> граней, и для него справедлива формула Эйлера. Добавим новую грань (пунктирная линия на рис.2), проводя по внешней грани <tex>F_{\infty}</tex> некоторую элементарную цепь, соединяющую две вершины максимального цикла графа <tex>G</tex>. Если эта цепь имеет <tex>r</tex> ребер, то необходимо добавить <tex>r - 1</tex> новых вершин и одну новую грань. Ясно, что формула Эйлера останется справедливой и для нового графа, так как <tex>V' - E' + F' = (V + r - 1) - (E + r) + (F + 1) = V - E + F = 2</tex> |
}} | }} | ||
| + | |||
| + | {|align="center" | ||
| + | |-valign="top" | ||
| + | |[[Файл:Eulerformul1.png|300px|thumb|рис. 1]] | ||
| + | |[[Файл:Eulerformul2.png|300px|thumb|рис. 2]] | ||
| + | |} | ||
| + | |||
{{Теорема | {{Теорема | ||
| + | |id=EulerFormulaCons | ||
|about= | |about= | ||
| − | + | следствие из формулы Эйлера | |
|statement= | |statement= | ||
| − | Пусть <tex>G</tex> | + | Пусть <tex>G</tex> связный [[Укладка графа на плоскости|планарный]] обыкновенный граф с <tex>V</tex> вершинами (<tex>V \geqslant 3</tex>), <tex>E</tex> ребрами и <tex>F</tex> гранями. Тогда <tex>E \leqslant 3V - 6</tex> |
|proof= | |proof= | ||
| − | Поскольку <tex>G</tex> не содержит петель и кратных ребер, то каждая грань граничит хотя бы с тремя ребрами. Пусть, двигаясь вдоль <tex>i</tex>-й грани мы пройдем <tex>l_i</tex> ребер. Очевидно, что <tex>\ | + | Поскольку <tex>G</tex> не содержит петель и кратных ребер, то каждая грань граничит хотя бы с тремя ребрами. Пусть, двигаясь вдоль <tex>i</tex>-й грани мы пройдем <tex>l_i</tex> ребер. Очевидно, что <tex>\sum \limits_{i=1}^{F}l_i = 2E</tex>. Поскольку <tex>l_i \geqslant 3 \hspace{3pt} (i = 1..F)</tex>, получаем <tex>3F \leqslant 2E</tex>. Из формулы Эйлера <tex>3E - 3V + 6 = 3F \leqslant 2E</tex>, то есть <tex>E \leqslant 3V - 6</tex>. |
}} | }} | ||
| − | == | + | ==Трехмерный случай== |
| − | * Асанов М,, Баранский В., Расин В. - Дискретная математика - Графы, матроиды, алгоритмы | + | |
| − | * О.Оре - Графы и их применение | + | Покажем, что в трехмерном случае так же имеет место формула Эйлера. |
| + | |||
| + | {{Теорема | ||
| + | |about= | ||
| + | формула Эйлера для многогранников | ||
| + | |statement= | ||
| + | Для любого выпуклого многогранника имеет место равенство <tex>V - E + F = 2</tex>, где <tex>V</tex> {{---}} число вершин, <tex>E</tex> {{---}} число ребер и <tex>F</tex> {{---}} число граней данного многогранника. | ||
| + | |proof= | ||
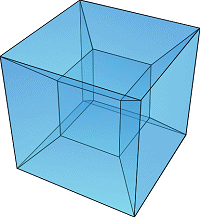
| + | [[Файл:Hypercube.gif|350px|thumb|right|Пример невыпуклого многоугольника для которого <tex dpi = 100>V - E + F = 0</tex>. Многоугольник получен путем вырезания куба внутри куба.]] | ||
| + | Для доказательства соотношения Эйлера представим поверхность выпуклого многогранника сделанной из эластичного материала. Удалим (вырежем) одну из его граней и оставшуюся поверхность растянем на плоскости. Получим планарный граф, содержащий <tex>F' = F - 1</tex> внутренних граней, <tex>V</tex> вершин и <tex>E</tex> ребер. | ||
| + | |||
| + | Тогда справедливо уже доказанное соотношение: <tex>V - E + F ' = 1 </tex>. | ||
| + | |||
| + | Подставляем <tex>F' = F - 1</tex> и получаем <tex>V - E + F = 2</tex>. | ||
| + | }} | ||
| + | |||
| + | {{Теорема | ||
| + | |about= | ||
| + | следствие из формулы Эйлера для многогранников | ||
| + | |statement= | ||
| + | В любом выпуклом многограннике имеется или треугольная грань, или трехгранный угол. Более того, число треугольных граней плюс число трехгранных углов больше или равно восьми. | ||
| + | |proof= | ||
| + | Обозначим через <tex>V_{i}</tex> число вершин выпуклого многогранника, в которых сходится <tex>i</tex> ребер. Тогда для общего числа вершин <tex>V</tex> имеет место равенство <tex>V = V_{3} + V_{4} + V_{5} + \dots</tex> | ||
| + | |||
| + | Аналогично, обозначим через <tex>F_{i}</tex> число граней выпуклого многогранника, у которых имеется <tex>i</tex> ребер. Тогда для общего числа граней <tex>F</tex> имеет место равенство <tex>F = F_{3} + F_{4} + F_{5} + \dots</tex> | ||
| + | |||
| + | Посчитаем число ребер <tex>E</tex> многогранника. Имеем: <tex>3V_{3} + 4V_{4} + 5V_{5} + \dots = 2E</tex>, <tex>3F_{3} + 4F_{4} + 5F_{5} + \dots = 2E</tex>. | ||
| + | |||
| + | По теореме Эйлера выполняется равенство <tex>4V - 4E + 4F = 8</tex>. Подставляя вместо <tex>V</tex>, <tex>E</tex> и <tex>F</tex> их выражения, получим: | ||
| + | |||
| + | <tex>4V_{3} + 4V_{4} + 4V_{5} + \dots - (3V_{3} + 4V_{4} + 5V_{5} + \dots) - (3F_{3} + 4F_{4} + 5F_{5} + \dots) + 4F_{3} + 4F_{4} + 4F_{5} + \dots = 8</tex>. | ||
| + | Следовательно, <tex>V_{3} + F_{3} = 8 + V_{5} + \dots + F_{5} + \dots </tex>, значит, число треугольных граней плюс число трехгранных углов больше или равно восьми.}} | ||
| + | |||
| + | ==Источники информации== | ||
| + | * Асанов М,, Баранский В., Расин В. {{---}} Дискретная математика {{---}} Графы, матроиды, алгоритмы (стр. 104-107) | ||
| + | * О.Оре {{---}} Графы и их применение (стр. 131-135) | ||
| + | *[https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%AD%D0%B9%D0%BB%D0%B5%D1%80%D0%B0_%D0%B4%D0%BB%D1%8F_%D0%BC%D0%BD%D0%BE%D0%B3%D0%BE%D0%B3%D1%80%D0%B0%D0%BD%D0%BD%D0%B8%D0%BA%D0%BE%D0%B2 Википедия {{---}} Теорема Эйлера для многоугольников] | ||
| + | * [http://www.geometry2006.narod.ru/Lecture/Mnogogr/Mnogogr.htm Выпуклые многогранники] | ||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Укладки графов ]] | [[Категория: Укладки графов ]] | ||
Текущая версия на 19:39, 4 сентября 2022
Двумерный случай
| Теорема (формула Эйлера): |
| Доказательство: |
|
Воспользуемся методом математической индукции по количеству граней графа.
|
| Теорема (следствие из формулы Эйлера): |
Пусть связный планарный обыкновенный граф с вершинами (), ребрами и гранями. Тогда |
| Доказательство: |
| Поскольку не содержит петель и кратных ребер, то каждая грань граничит хотя бы с тремя ребрами. Пусть, двигаясь вдоль -й грани мы пройдем ребер. Очевидно, что . Поскольку , получаем . Из формулы Эйлера , то есть . |
Трехмерный случай
Покажем, что в трехмерном случае так же имеет место формула Эйлера.
| Теорема (формула Эйлера для многогранников): |
Для любого выпуклого многогранника имеет место равенство , где — число вершин, — число ребер и — число граней данного многогранника. |
| Доказательство: |
|
Для доказательства соотношения Эйлера представим поверхность выпуклого многогранника сделанной из эластичного материала. Удалим (вырежем) одну из его граней и оставшуюся поверхность растянем на плоскости. Получим планарный граф, содержащий внутренних граней, вершин и ребер. Тогда справедливо уже доказанное соотношение: . Подставляем и получаем . |
| Теорема (следствие из формулы Эйлера для многогранников): |
В любом выпуклом многограннике имеется или треугольная грань, или трехгранный угол. Более того, число треугольных граней плюс число трехгранных углов больше или равно восьми. |
| Доказательство: |
|
Обозначим через число вершин выпуклого многогранника, в которых сходится ребер. Тогда для общего числа вершин имеет место равенство Аналогично, обозначим через число граней выпуклого многогранника, у которых имеется ребер. Тогда для общего числа граней имеет место равенство Посчитаем число ребер многогранника. Имеем: , . По теореме Эйлера выполняется равенство . Подставляя вместо , и их выражения, получим: . Следовательно, , значит, число треугольных граней плюс число трехгранных углов больше или равно восьми. |
Источники информации
- Асанов М,, Баранский В., Расин В. — Дискретная математика — Графы, матроиды, алгоритмы (стр. 104-107)
- О.Оре — Графы и их применение (стр. 131-135)
- Википедия — Теорема Эйлера для многоугольников
- Выпуклые многогранники