|
|
| Строка 1: |
Строка 1: |
| − | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;"
| |
| − | |+
| |
| − | |-align="center"
| |
| − | |'''НЕТ ВОЙНЕ'''
| |
| − | |-style="font-size: 16px;"
| |
| − | |
| |
| − | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян.
| |
| − |
| |
| − | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием.
| |
| − |
| |
| − | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей.
| |
| − |
| |
| − | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить.
| |
| − |
| |
| − | ''Антивоенный комитет России''
| |
| − | |-style="font-size: 16px;"
| |
| − | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.
| |
| − | |-style="font-size: 16px;"
| |
| − | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки].
| |
| − | |}
| |
| − |
| |
| | == Описание == | | == Описание == |
| | {|align="center" | | {|align="center" |
Текущая версия на 19:39, 4 сентября 2022
Описание
| Сумма Минковского позволяет решать задачу Motion Planning, в случае, когда робота нельзя поворачивать. Таким образом, каждой точке [math](x, y)[/math] ставится в соответствие фигура робота [math]R(x, y)[/math], с точкой привязки помещенной в точку [math](x, y)[/math].
| Определение: |
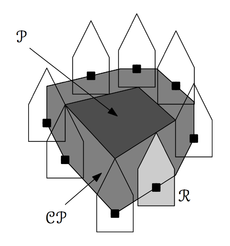
| Для заданного робота [math]R[/math] и препятствия [math]P[/math], К-препятствием называется множество точек, будучи помещенным в которые, робот заденет препятствие:
[math]CP := \{(x, y) : R(x, y) \cap P \neq \varnothing\}[/math] |
|
|
| Определение: |
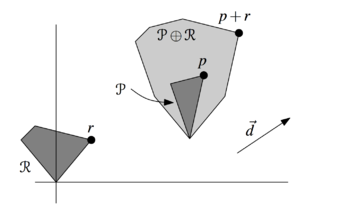
| Суммой Минковского двух множеств [math]S_1 \subset R^2, S_2 \subset R^2[/math] называется множество [math]S_1 \oplus S_2 := \{p + q : p \in S_1, q \in S_2\}[/math], где [math]p + q[/math] обозначает векторную сумму. |
| Определение: |
| Отрицанием множества [math]S \subset R^2[/math] называется множество [math]-S := \{-p : p \in S\}[/math], где [math]-p[/math] обозначает векторное отрицание. |
| Теорема: |
Для заданного робота [math]R[/math] и препятствия [math]P[/math], К-препятствием является множество [math]P \oplus (-R(0, 0))[/math]. |
| Доказательство: |
| [math]\triangleright[/math] |
|
Необходимо доказать, что робот [math]R(x, y)[/math] пересекает препятствие [math]P[/math] в том и только в том случае, если [math](x, y) \in P \oplus (-R(0, 0))[/math].
Пусть робот задевает препятствие, и точка [math]q = (q_x , q_y)[/math] является точкой пересечения. Тогда, так как [math]q \in R(x, y)[/math], то [math](q_x - x, q_y - y) \in R(0,0)[/math], или [math](x - q_x , y - q_y) \in -R(0,0)[/math]. А заметив, что [math]q \in P[/math], получаем [math](x, y) \in P \oplus (-R(0,0))[/math].
В обратную сторону, пусть [math](x, y) \in P \oplus (-R(0,0))[/math], тогда существуют точки [math](r_x , r_y) \in R(0, 0)[/math] и [math](p_x , p_y) \in P[/math] такие, что [math](x, y) = (p_x - r_x , p_y - r_y)[/math] или [math](p_x , p_y) = (x + r_x , y + r_y)[/math], а это означает, что [math]R(x, y)[/math] пересекает [math]P[/math]. |
| [math]\triangleleft[/math] |
Допустим, для простоты, что робот и все препятствия выпуклые, а позже обобщим для невыпуклых фигур.
| Теорема: |
Пусть заданы две выпуклые фигуры [math]P[/math] и [math]R[/math], с числом вершин [math]n[/math] и [math]m[/math] соответственно. Тогда суммой Минковского [math]P \oplus R[/math] является выпуклая фигура с не более чем [math]m + n[/math] вершинами. |
| Доказательство: |
| [math]\triangleright[/math] |
|
Для начала заметим, что любая крайняя точка в направлении вектора [math]\vec{d}[/math] есть сумма крайних точек фигур в этом направлении. Убедиться в этом можно спроецировав обе фигуры на вектор [math]\vec{d}[/math].
Теперь рассмотрим произвольное ребро [math]e[/math] из [math]P \oplus R[/math]. Оно является крайним в направлении к своей нормали, а значит оно образовано крайними точками фигур, и хотя бы у одной из фигур должно быть ребро, которое является крайним в этом направлении. Сопоставим [math]e[/math] с этим ребром. Тогда сопоставив таким образом всем ребрам [math]P \oplus R[/math] ребра исходных фигур, получаем что всего ребер в [math]P \oplus R[/math] не более чем [math]m + n[/math], так как каждое ребро исходных фигур использовалось не более раза. |
| [math]\triangleleft[/math] |
Псевдокод
i = j = 0
V[n] = V[0], V[n+1] = V[1], W[m] = W[0], W[m+1] = W[1]
while i < n or j < m do
add V[i]+W[j] to answer
if angle(V[i], V[i+1]) < angle(W[j], W[j+1])
++i
else if angle(V[i], V[i+1]) > angle(W[j], W[j+1])
++j
else
++i, ++j
Здесь множества точек [math]V[/math] и [math]W[/math] отсортированы в порядке обхода против часовой стрелки, причем первым элементом в обоих массивах является самая левая нижняя точка множества. Функция angle возвращает значение полярного угла вектора, заданного ее аргументами.
Корректность алгоритма следует из доказательства предыдущей теоремы, а время работы равно [math]O(n + m)[/math], так как на каждой итерации хотя бы один из индексов [math]i[/math] и [math]j[/math] увеличивается.
Случай невыпуклых фигур
Для начала заметим следующий факт:
[math]S_1 \oplus (S_2 \cup S_3) = (S_1 \oplus S_2) \cup (S_1 \oplus S_3)[/math]
В случае, когда одна из фигур невыпукла, её сначала надо затриангулировать, получив [math]n-2[/math] треугольников. После этого, уже известным алгоритмом, надо построить [math]n-2[/math] выпуклых фигур с не более чем [math]m+3[/math] вершинами, которые будут суммами Минковского соответствующих треугольников. Объединение этих выпуклых фигур будет состоять из [math]O(nm)[/math] вершин.
В случае, когда обе фигуры невыпуклы, обе эти фигуры надо затриангулировать, получив [math]n-2[/math] и [math]m-2[/math] треугольников соответственно. Построив суммы Минковского множеств этих треугольников получим [math](n-2)(m-2)[/math] выпуклых фигур, объединение которых состоит из [math]O(n^2m^2)[/math] вершин.
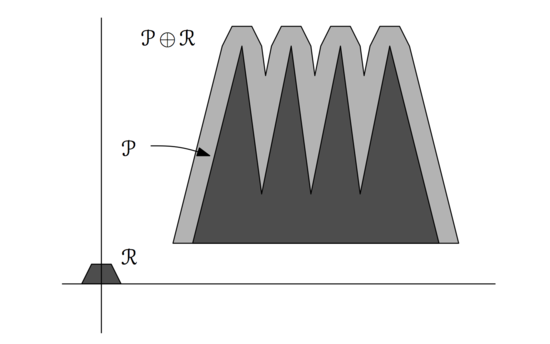 Пример суммы Минковского с O(nm) вершинами |
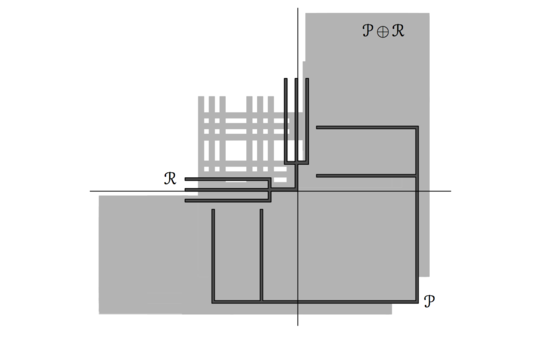 Пример суммы Минковского с O(n 2m 2) вершинами |
Ссылки
- Английская википедия
- de Berg, van Kreveld, Overmars, Schwarzkopf "Computational Geometry Algorithms and Applications", p. 290