Алгоритм Хаффмана — различия между версиями
Yulya3102 (обсуждение | вклад) м |
м (rollbackEdits.php mass rollback) |
||
| (не показано 35 промежуточных версий 15 участников) | |||
| Строка 1: | Строка 1: | ||
| − | ''''' | + | '''Алгоритм Хаффмана''' (англ. ''Huffman's algorithm'') — алгоритм [[Задача_об_оптимальном_префиксном_коде_с_сохранением_порядка._Монотонность_точки_разреза | оптимального префиксного кодирования]] алфавита. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. Используется во многих программах сжатия данных, например, PKZIP 2, LZH и др. |
== Определение == | == Определение == | ||
| Строка 5: | Строка 5: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | Пусть <tex>A=\{a_{1},a_{2}, | + | Пусть <tex>A=\{a_{1},a_{2}, \ldots ,a_{n}\}</tex> — алфавит из <tex>n</tex> различных символов, <tex>W=\{w_{1},w_{2}, \ldots ,w_{n}\}</tex> — соответствующий ему набор положительных целых весов. Тогда набор бинарных кодов <tex>C=\{c_{1},c_{2}, \ldots ,c_{n}\}</tex>, где <tex>c_{i}</tex> является кодом для символа <tex>a_{i}</tex>, такой, что: |
| − | + | :* <tex>c_{i}</tex> не является префиксом для <tex>c_{j}</tex>, при <tex>i \ne j</tex>, | |
| − | + | :* cумма <tex>\sum\limits_{i \in [1, n]} w_{i}\cdot |c_{i}|</tex> минимальна (<tex>|c_{i}|</tex> — длина кода <tex>c_{i}</tex>), | |
называется '''кодом Хаффмана'''. | называется '''кодом Хаффмана'''. | ||
}} | }} | ||
| − | == Алгоритм == | + | == Алгоритм построения бинарного кода Хаффмана == |
| − | Построение кода Хаффмана сводится к построению соответствующего бинарного дерева по следующему алгоритму: | + | Построение кода Хаффмана сводится к построению соответствующего [[ Двоичная_куча | бинарного дерева]] по следующему алгоритму: |
| − | + | # Составим [[Список | список]] кодируемых символов, при этом будем рассматривать один символ как дерево, состоящее из одного элемента c весом, равным частоте появления символа в строке. | |
| + | # Из списка выберем два узла с наименьшим весом. | ||
| + | # Сформируем новый узел с весом, равным сумме весов выбранных узлов, и присоединим к нему два выбранных узла в качестве детей. | ||
| + | # Добавим к списку только что сформированный узел вместо двух объединенных узлов. | ||
| + | # Если в списке больше одного узла, то повторим пункты со второго по пятый. | ||
| − | + | === Время работы === | |
| + | Если сортировать элементы после каждого суммирования или использовать [[Приоритетные_очереди | приоритетную очередь]], то алгоритм будет работать за время <tex>O(N \log N)</tex>.Такую асимптотику можно [[Алгоритм_Хаффмана_за_O(n) |улучшить до <tex>O(N)</tex>]], используя обычные массивы. | ||
| − | + | === Пример === | |
| − | + | [[Файл:Huffman_abracadabra.jpg|400px|thumb|right|Дерево Хаффмана для слова <tex>abracadabra</tex>]] | |
| − | + | Закодируем слово <tex>abracadabra</tex>. Тогда алфавит будет <tex>A= \{a, b, r, c, d\} </tex>, а набор весов (частота появления символов алфавита в кодируемом слове) <tex>W=\{5, 2, 2, 1, 1\}</tex>: | |
| − | + | В дереве Хаффмана будет <tex>5</tex> узлов: | |
| − | < | + | {| class="wikitable" |
| − | {| | + | ! Узел || a || b || r || с || d |
| − | | | + | |- |
| + | | Вес || 5 || 2 || 2 || 1 || 1 | ||
| + | |} | ||
| + | |||
| + | По алгоритму возьмем два символа с наименьшей частотой {{---}} это <tex>c</tex> и <tex>d</tex>. Сформируем из них новый узел <tex>cd</tex> весом <tex>2</tex> и добавим его к списку узлов: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | ! Узел || a || b || r || cd | ||
| + | |- | ||
| + | | Вес || 5 || 2 || 2 || 2 | ||
| + | |} | ||
| + | |||
| + | Затем опять объединим в один узел два минимальных по весу узла {{---}} <tex>r</tex> и <tex>cd</tex>: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | ! Узел || a || rcd || b | ||
| + | |- | ||
| + | | Вес || 5 || 4 || 2 | ||
| + | |} | ||
| + | |||
| + | Еще раз повторим эту же операцию, но для узлов <tex>rcd</tex> и <tex>b</tex>: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | ! Узел || brcd || a | ||
| + | |- | ||
| + | | Вес || 6 || 5 | ||
|} | |} | ||
| − | </ | + | |
| − | + | На последнем шаге объединим два узла {{---}} <tex>brcd</tex> и <tex>a</tex>: | |
{| class="wikitable" | {| class="wikitable" | ||
| − | ! | + | ! Узел || abrcd |
|- | |- | ||
| − | | | + | | Вес || 11 |
|} | |} | ||
| − | + | Остался один узел, значит, мы пришли к корню дерева Хаффмана (смотри рисунок). Теперь для каждого символа выберем кодовое слово (бинарная последовательность, обозначающая путь по дереву к этому символу от корня): | |
| − | |||
| − | |||
{| class="wikitable" | {| class="wikitable" | ||
| − | ! a || b || | + | ! Символ || a || b || r || с || d |
|- | |- | ||
| − | | 0 || 11 || | + | | Код || 0 || 11 || 101 || 1000 || 1001 |
|} | |} | ||
| + | |||
| + | Таким образом, закодированное слово <tex>abracadabra</tex> будет выглядеть как <tex>01110101000010010111010</tex>. Длина закодированного слова {{---}} <tex>23</tex> бита. Стоит заметить, что если бы мы использовали алгоритм кодирования с одинаковой длиной всех кодовых слов, то закодированное слово заняло бы <tex>33</tex> бита, что существенно больше. | ||
== Корректность алгоритма Хаффмана == | == Корректность алгоритма Хаффмана == | ||
| − | + | ||
| − | Чтобы доказать корректность алгоритма Хаффмана, покажем, что в задаче о построении оптимального префиксного кода проявляются свойства жадного выбора и оптимальной подструктуры. В сформулированной ниже лемме показано соблюдение свойства жадного выбора. | + | Чтобы доказать корректность алгоритма Хаффмана, покажем, что в задаче о построении оптимального префиксного кода проявляются свойства жадного выбора и оптимальной подструктуры. В сформулированной ниже лемме показано соблюдение свойства жадного выбора. |
{{Лемма | {{Лемма | ||
| Строка 65: | Строка 95: | ||
Тогда для алфавита <tex>C</tex> существует оптимальный префиксный код, кодовые слова символов <tex>x</tex> и <tex>y</tex> в котором имеют одинаковую максимальную длину и отличаются лишь последним битом. | Тогда для алфавита <tex>C</tex> существует оптимальный префиксный код, кодовые слова символов <tex>x</tex> и <tex>y</tex> в котором имеют одинаковую максимальную длину и отличаются лишь последним битом. | ||
|proof= | |proof= | ||
| − | Возьмем дерево <tex>T</tex>, представляющее произвольный оптимальный префиксный код | + | Возьмем дерево <tex>T</tex>, представляющее произвольный оптимальный префиксный код для алфавита <tex>C</tex>. Преобразуем его в дерево, представляющее другой оптимальный префиксный код, в котором символы <tex>x</tex> и <tex>y</tex> — листья с общим родительским узлом, находящиеся на максимальной глубине. |
| − | Пусть <tex>a</tex> и <tex>b</tex> | + | Пусть символы <tex>a</tex> и <tex>b</tex> имеют общий родительский узел и находятся на максимальной глубине дерева <tex>T</tex>. Предположим, что <tex>f[a] \leqslant f[b]</tex> и <tex>f[x] \leqslant f[y]</tex>. Так как <tex>f[x]</tex> и <tex>f[y]</tex> — две наименьшие частоты, а <tex>f[a]</tex> и <tex>f[b]</tex> — две произвольные частоты, то выполняются отношения <tex>f[x] \leqslant f[a]</tex> и <tex>f[y] \leqslant f[b]</tex>. Пусть дерево <tex>T'</tex> — дерево, полученное из <tex>T</tex> путем перестановки листьев <tex>a</tex> и <tex>x</tex>, а дерево <tex>T''</tex> — дерево полученное из <tex>T'</tex> перестановкой листьев <tex>b</tex> и <tex>y</tex>. Разность стоимостей деревьев <tex>T</tex> и <tex>T'</tex> равна: |
| − | + | <tex>B(T) - B(T') = \sum\limits_{c \in C} f(c)d_T(c) - \sum\limits_{c \in C} f(c)d_{T'}(c) = (f[a] - f[x])(d_T(a) - d_T(x)),</tex> | |
| − | + | что больше либо равно <tex>0</tex>, так как величины <tex>f[a] - f[x]</tex> и <tex>d_T(a) - d_T(x)</tex> неотрицательны. Величина <tex>f[a] - f[x]</tex> неотрицательна, потому что <tex>x</tex> — лист с минимальной частотой, а величина <tex>d_T(a) - d_T(x)</tex> является неотрицательной, так как лист <tex>a</tex> находится на максимальной глубине в дереве <tex>T</tex>. Точно так же перестановка листьев <tex>y</tex> и <tex>b</tex> не будет приводить к увеличению стоимости. Таким образом, разность <tex>B(T') - B(T'')</tex> тоже будет неотрицательной. | |
| − | <tex>B(T | + | Таким образом, выполняется неравенство <tex>B(T'') \leqslant B(T)</tex>. С другой стороны, <tex>T</tex> — оптимальное дерево, поэтому должно выполняться неравенство <tex>B(T) \leqslant B(T'')</tex>. Отсюда следует, что <tex>B(T) = B(T'')</tex>. Значит, <tex>T''</tex> — дерево, представляющее оптимальный префиксный код, в котором символы <tex>x</tex> и <tex>y</tex> имеют одинаковую максимальную длину, что и доказывает лемму. |
| − | + | }} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Лемма | {{Лемма | ||
|id=lemma2 | |id=lemma2 | ||
|about=2 | |about=2 | ||
|statement=Пусть дан алфавит <tex>C</tex>, в котором для каждого символа <tex>c \in C</tex> определены частоты <tex>f[c]</tex>. Пусть <tex>x</tex> и <tex>y</tex> — два символа из алфавита <tex>C</tex> с минимальными частотами. Пусть <tex>C'</tex> — алфавит, полученный из алфавита <tex>C</tex> путем удаления символов <tex>x</tex> и <tex>y</tex> и добавления нового символа <tex>z</tex>, так что <tex>C' = C \backslash \{ x, y \} \cup {z}</tex>. По определению частоты <tex>f</tex> в алфавите <tex>C'</tex> совпадают с частотами в алфавите <tex>C</tex>, за исключением частоты <tex>f[z] = f[x] + f[y]</tex>. Пусть <tex>T'</tex> — произвольное дерево, представляющее оптимальный префиксный код для алфавита <tex>C'</tex> Тогда дерево <tex>T</tex>, полученное из дерева <tex>T'</tex> путем замены листа <tex>z</tex> внутренним узлом с дочерними элементами <tex>x</tex> и <tex>y</tex>, представляет оптимальный префиксный код для алфавита <tex>C</tex>. | |statement=Пусть дан алфавит <tex>C</tex>, в котором для каждого символа <tex>c \in C</tex> определены частоты <tex>f[c]</tex>. Пусть <tex>x</tex> и <tex>y</tex> — два символа из алфавита <tex>C</tex> с минимальными частотами. Пусть <tex>C'</tex> — алфавит, полученный из алфавита <tex>C</tex> путем удаления символов <tex>x</tex> и <tex>y</tex> и добавления нового символа <tex>z</tex>, так что <tex>C' = C \backslash \{ x, y \} \cup {z}</tex>. По определению частоты <tex>f</tex> в алфавите <tex>C'</tex> совпадают с частотами в алфавите <tex>C</tex>, за исключением частоты <tex>f[z] = f[x] + f[y]</tex>. Пусть <tex>T'</tex> — произвольное дерево, представляющее оптимальный префиксный код для алфавита <tex>C'</tex> Тогда дерево <tex>T</tex>, полученное из дерева <tex>T'</tex> путем замены листа <tex>z</tex> внутренним узлом с дочерними элементами <tex>x</tex> и <tex>y</tex>, представляет оптимальный префиксный код для алфавита <tex>C</tex>. | ||
| − | |proof=Сначала покажем, что стоимость <tex>B(T)</tex> дерева <tex>T</tex> | + | |proof= |
| − | <tex>f[x]d_T(x) + f[y] | + | Сначала покажем, что стоимость <tex>B(T)</tex> дерева <tex>T</tex> может быть выражена через стоимость <tex>B(T')</tex> дерева <tex>T'</tex>. Для каждого символа <tex>c \in C \backslash \{x, y \}</tex> верно <tex>d_T(C) = d_{T'}</tex>, значит, <tex>f[c]d_T(c) = f[c]d_{T'}(c)</tex>. Так как <tex>d_T(x) = d_T(y) = d_{T'} (z) + 1</tex>, то |
| − | + | ||
| − | из | + | <tex>f[x]d_T(x) + f[y]d_T(y) = (f[x] + f[y])(d_{T'}(z) + 1) = f[z]d_{T'}(z) + (f[x] + f[y])</tex> |
| + | |||
| + | из чего следует, что | ||
| + | |||
<tex> B(T) = B(T') + f[x] + f[y] </tex> | <tex> B(T) = B(T') + f[x] + f[y] </tex> | ||
| − | + | или | |
| + | |||
| + | <tex> B(T') = B(T) - f[x] - f[y] </tex> | ||
| + | |||
| + | Докажем лемму от противного. Предположим, что дерево <tex>T</tex> не представляет оптимальный префиксный код для алфавита <tex>C</tex>. Тогда существует дерево <tex>T''</tex> такое, что <tex>B(T'') < B(T)</tex>. Согласно лемме (1), элементы <tex>x</tex> и <tex>y</tex> можно считать дочерними элементами одного узла. Пусть дерево <tex>T'''</tex> получено из дерева <tex>T''</tex> заменой элементов <tex>x</tex> и <tex>y</tex> листом <tex>z</tex> с частотой <tex>f[z] = f[x] + f[y]</tex>. Тогда | ||
| − | <tex> B(T') = B(T) - f[x] - f[y] </tex> | + | <tex>B(T''') = B(T'') - f[x] - f[y] < B(T) - f[x] - f[y] = B(T')</tex>, |
| − | + | что противоречит предположению о том, что дерево <tex>T'</tex> представляет оптимальный префиксный код для алфавита <tex>C'</tex>. Значит, наше предположение о том, что дерево <tex>T</tex> не представляет оптимальный префиксный код для алфавита <tex>C</tex>, неверно, что и доказывает лемму. | |
| − | |||
| − | что противоречит предположению о том, что дерево <tex>T'</tex> представляет оптимальный префиксный код для алфавита <tex>C'</tex>. | ||
}} | }} | ||
| Строка 108: | Строка 138: | ||
}} | }} | ||
| − | == | + | == См. также == |
| − | * Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — | + | *[[Оптимальное_хранение_словаря_в_алгоритме_Хаффмана | Оптимальное хранение словаря в алгоритме Хаффмана]] |
| + | |||
| + | == Источники информации == | ||
| + | |||
| + | * Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 459. — ISBN 5-8489-0857-4 | ||
| + | *[http://en.wikipedia.org/wiki/Huffman_coding Wikipedia — Huffman coding] | ||
| + | *[http://ru.wikipedia.org/wiki/%C4%E2%EE%E8%F7%ED%EE%E5_%E4%E5%F0%E5%E2%EE Википедия — Бинарное дерево] | ||
| + | *[http://ru.wikipedia.org/wiki/Префиксный_код Википедия — Префиксный код] | ||
| + | |||
| + | [[Категория: Дискретная математика и алгоритмы]] | ||
| − | [[Категория: Алгоритмы сжатия ]] | + | [[Категория:Алгоритмы сжатия]] |
Текущая версия на 19:41, 4 сентября 2022
Алгоритм Хаффмана (англ. Huffman's algorithm) — алгоритм оптимального префиксного кодирования алфавита. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. Используется во многих программах сжатия данных, например, PKZIP 2, LZH и др.
Содержание
Определение
| Определение: |
Пусть — алфавит из различных символов, — соответствующий ему набор положительных целых весов. Тогда набор бинарных кодов , где является кодом для символа , такой, что:
|
Алгоритм построения бинарного кода Хаффмана
Построение кода Хаффмана сводится к построению соответствующего бинарного дерева по следующему алгоритму:
- Составим список кодируемых символов, при этом будем рассматривать один символ как дерево, состоящее из одного элемента c весом, равным частоте появления символа в строке.
- Из списка выберем два узла с наименьшим весом.
- Сформируем новый узел с весом, равным сумме весов выбранных узлов, и присоединим к нему два выбранных узла в качестве детей.
- Добавим к списку только что сформированный узел вместо двух объединенных узлов.
- Если в списке больше одного узла, то повторим пункты со второго по пятый.
Время работы
Если сортировать элементы после каждого суммирования или использовать приоритетную очередь, то алгоритм будет работать за время .Такую асимптотику можно улучшить до , используя обычные массивы.
Пример
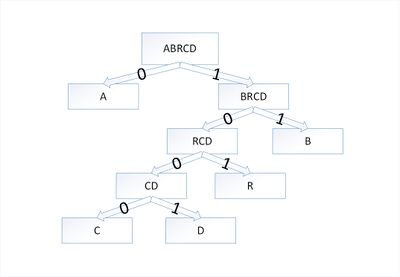
Закодируем слово . Тогда алфавит будет , а набор весов (частота появления символов алфавита в кодируемом слове) :
В дереве Хаффмана будет узлов:
| Узел | a | b | r | с | d |
|---|---|---|---|---|---|
| Вес | 5 | 2 | 2 | 1 | 1 |
По алгоритму возьмем два символа с наименьшей частотой — это и . Сформируем из них новый узел весом и добавим его к списку узлов:
| Узел | a | b | r | cd |
|---|---|---|---|---|
| Вес | 5 | 2 | 2 | 2 |
Затем опять объединим в один узел два минимальных по весу узла — и :
| Узел | a | rcd | b |
|---|---|---|---|
| Вес | 5 | 4 | 2 |
Еще раз повторим эту же операцию, но для узлов и :
| Узел | brcd | a |
|---|---|---|
| Вес | 6 | 5 |
На последнем шаге объединим два узла — и :
| Узел | abrcd |
|---|---|
| Вес | 11 |
Остался один узел, значит, мы пришли к корню дерева Хаффмана (смотри рисунок). Теперь для каждого символа выберем кодовое слово (бинарная последовательность, обозначающая путь по дереву к этому символу от корня):
| Символ | a | b | r | с | d |
|---|---|---|---|---|---|
| Код | 0 | 11 | 101 | 1000 | 1001 |
Таким образом, закодированное слово будет выглядеть как . Длина закодированного слова — бита. Стоит заметить, что если бы мы использовали алгоритм кодирования с одинаковой длиной всех кодовых слов, то закодированное слово заняло бы бита, что существенно больше.
Корректность алгоритма Хаффмана
Чтобы доказать корректность алгоритма Хаффмана, покажем, что в задаче о построении оптимального префиксного кода проявляются свойства жадного выбора и оптимальной подструктуры. В сформулированной ниже лемме показано соблюдение свойства жадного выбора.
| Лемма (1): |
Пусть — алфавит, каждый символ которого встречается с частотой . Пусть и — два символа алфавита с самыми низкими частотами.
Тогда для алфавита существует оптимальный префиксный код, кодовые слова символов и в котором имеют одинаковую максимальную длину и отличаются лишь последним битом. |
| Доказательство: |
|
Возьмем дерево , представляющее произвольный оптимальный префиксный код для алфавита . Преобразуем его в дерево, представляющее другой оптимальный префиксный код, в котором символы и — листья с общим родительским узлом, находящиеся на максимальной глубине. Пусть символы и имеют общий родительский узел и находятся на максимальной глубине дерева . Предположим, что и . Так как и — две наименьшие частоты, а и — две произвольные частоты, то выполняются отношения и . Пусть дерево — дерево, полученное из путем перестановки листьев и , а дерево — дерево полученное из перестановкой листьев и . Разность стоимостей деревьев и равна:
что больше либо равно , так как величины и неотрицательны. Величина неотрицательна, потому что — лист с минимальной частотой, а величина является неотрицательной, так как лист находится на максимальной глубине в дереве . Точно так же перестановка листьев и не будет приводить к увеличению стоимости. Таким образом, разность тоже будет неотрицательной. Таким образом, выполняется неравенство . С другой стороны, — оптимальное дерево, поэтому должно выполняться неравенство . Отсюда следует, что . Значит, — дерево, представляющее оптимальный префиксный код, в котором символы и имеют одинаковую максимальную длину, что и доказывает лемму. |
| Лемма (2): |
Пусть дан алфавит , в котором для каждого символа определены частоты . Пусть и — два символа из алфавита с минимальными частотами. Пусть — алфавит, полученный из алфавита путем удаления символов и и добавления нового символа , так что . По определению частоты в алфавите совпадают с частотами в алфавите , за исключением частоты . Пусть — произвольное дерево, представляющее оптимальный префиксный код для алфавита Тогда дерево , полученное из дерева путем замены листа внутренним узлом с дочерними элементами и , представляет оптимальный префиксный код для алфавита . |
| Доказательство: |
|
Сначала покажем, что стоимость дерева может быть выражена через стоимость дерева . Для каждого символа верно , значит, . Так как , то
из чего следует, что
или
Докажем лемму от противного. Предположим, что дерево не представляет оптимальный префиксный код для алфавита . Тогда существует дерево такое, что . Согласно лемме (1), элементы и можно считать дочерними элементами одного узла. Пусть дерево получено из дерева заменой элементов и листом с частотой . Тогда , что противоречит предположению о том, что дерево представляет оптимальный префиксный код для алфавита . Значит, наше предположение о том, что дерево не представляет оптимальный префиксный код для алфавита , неверно, что и доказывает лемму. |
| Теорема: |
Алгоритм Хаффмана дает оптимальный префиксный код. |
| Доказательство: |
| Справедливость теоремы непосредственно следует из лемм (1) и (2) |
См. также
Источники информации
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 459. — ISBN 5-8489-0857-4
- Wikipedia — Huffman coding
- Википедия — Бинарное дерево
- Википедия — Префиксный код