Сжатое суффиксное дерево — различия между версиями
(→Поиск строки максимальной длины, ветвящейся влево и вправо 1.3.3) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 66 промежуточных версий 12 участников) | |||
| Строка 1: | Строка 1: | ||
| − | [[Суффиксный бор|Суффиксный бор]] {{---}} удобная структура данных для поиска подстроки в строке, но она требует порядка квадрата длины исходной строки памяти. Оптимизацией суффиксного бора, требующей линейное количество памяти, является '''сжатое суффиксное дерево''' рассматриваемое далее. | + | [[Суффиксный бор|Суффиксный бор]] {{---}} удобная структура данных для поиска подстроки в строке, но она требует порядка квадрата длины исходной строки памяти. Оптимизацией суффиксного бора, требующей линейное количество памяти, является '''сжатое суффиксное дерево''' (англ. ''compressed suffix tree''), рассматриваемое далее. |
==Определение== | ==Определение== | ||
{{Определение | {{Определение | ||
| + | |neat = 1 | ||
| + | |id=suffix_tree | ||
|definition = | |definition = | ||
'''Суффиксное дерево''' (сжатое суффиксное дерево) <tex>T</tex> для строки <tex>s</tex> (где <tex>|s| = n</tex>) {{---}} дерево с <tex>n</tex> листьями, обладающее следующими свойствами: | '''Суффиксное дерево''' (сжатое суффиксное дерево) <tex>T</tex> для строки <tex>s</tex> (где <tex>|s| = n</tex>) {{---}} дерево с <tex>n</tex> листьями, обладающее следующими свойствами: | ||
| − | * | + | *каждая внутренняя вершина дерева имеет не меньше двух детей; |
| − | * | + | *каждое ребро помечено непустой подстрокой строки <tex>s</tex>; |
| − | * | + | *никакие два ребра, выходящие из одной вершины, не могут иметь пометок, начинающихся с одного и того же символа; |
| − | * | + | *дерево должно содержать все суффиксы строки <tex>s</tex>, причем каждый суффикс заканчивается точно в листе и нигде кроме него. |
| − | }} | + | }} |
| + | [[Файл:Suffix_tree_3.png|250px|thumb|Суффиксное дерево для строки <tex>xabxa</tex> с защитным символом]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| − | |||
'''Данное определение порождает следующую проблему:''' <br/> | '''Данное определение порождает следующую проблему:''' <br/> | ||
Рассмотрим дерево для строки <tex>xabxa</tex>: суффикс <tex>xa</tex> является префиксом суффикса <tex>xabxa</tex>, а, значит, этот суффикс не закачивается в листе. Для решения проблемы в конце строки <tex>s</tex> добавляют символ, не входящий в исходный алфавит: '''''защитный''''' символ. Обозначим его как <tex>\$</tex>. Любой суффикс строки с защитным символом действительно заканчивается в листе и только в листе, т. к. в такой строке не существует двух различных подстрок одинаковой длины, заканчивающихся на <tex>\$</tex>. | Рассмотрим дерево для строки <tex>xabxa</tex>: суффикс <tex>xa</tex> является префиксом суффикса <tex>xabxa</tex>, а, значит, этот суффикс не закачивается в листе. Для решения проблемы в конце строки <tex>s</tex> добавляют символ, не входящий в исходный алфавит: '''''защитный''''' символ. Обозначим его как <tex>\$</tex>. Любой суффикс строки с защитным символом действительно заканчивается в листе и только в листе, т. к. в такой строке не существует двух различных подстрок одинаковой длины, заканчивающихся на <tex>\$</tex>. | ||
Далее <tex>n</tex> {{---}} длина строки <tex>s</tex> с защитным символом. | Далее <tex>n</tex> {{---}} длина строки <tex>s</tex> с защитным символом. | ||
| + | <br/> | ||
| + | <br/> | ||
| + | <br/> | ||
| + | <br/> | ||
| + | <br/> | ||
| + | <br/> | ||
| + | <br/> | ||
| + | <br/> | ||
| + | <br/> | ||
| + | <br/> | ||
| − | == | + | ==Число вершин== |
| − | По определению, в суффиксном дереве содержится <tex>n</tex> листьев. Оценим | + | По определению, в суффиксном дереве содержится <tex>n</tex> листьев. Оценим число внутренних вершин такого дерева. |
{{Лемма | {{Лемма | ||
|statement= | |statement= | ||
| − | + | Число внутренних вершин дерева, каждая из которых имеет не менее двух детей, меньше числа листьев. | |
|proof= | |proof= | ||
| − | |||
| − | + | : Докажем лемму индукцией по числу листьев <tex>n</tex>. | |
| − | + | : '''База''' | |
| − | + | : При <tex>n = 2</tex> в дереве одна внутренняя вершина, следовательно утверждение верно. | |
| − | + | : '''Переход''' <tex>n \rightarrow n + 1</tex> | |
| − | + | : Возьмем вершину в дереве с <tex>n + 1</tex> листами, у которой два ребенка {{---}} листья. Рассмотрим возможные случаи: | |
| − | + | # У нее более двух детей. Тогда отрежем от нее лист. Получим дерево с <tex>n</tex> листьями, причем в нем число внутренних вершин такое же, как в исходном дереве. Но у полученного дерева по индукционному предположению менее <tex>n</tex> внутренних вершин, а, значит, и для исходного дерева лемма верна. | |
| + | # У нее ровно два ребенка. Отрежем их, получим дерево с <tex>n</tex> листьями, число внутренних вершин которого на <tex>1</tex> меньше, чем в исходном дереве. Тогда по индукционному предположению у него менее <tex>n</tex> внутренних вершин, значит, в исходном дереве их меньше <tex>n + 1</tex>. | ||
}} | }} | ||
==Занимаемая память== | ==Занимаемая память== | ||
| − | Представим дерево как двумерный массив размера <tex>|V| \times |\Sigma|</tex>, где <tex>|V|</tex> {{---}} | + | Представим дерево как двумерный массив размера <tex>|V| \times |\Sigma|</tex>, где <tex>|V|</tex> {{---}} число вершин в дереве, <tex>|\Sigma|</tex> {{---}} мощность алфавита. Для любого суффиксного дерева верна предыдущая лемма (у каждой вершины, по определению, не менее двух детей), значит, <tex>|V| = O(2 n)</tex>. Каждая <tex>a[i][j]</tex> ячейка содержит информацию о том, в какую вершину ведет ребро из <tex>i</tex>-ой вершины по <tex>j</tex>-ому символу и индексы <tex>l, r</tex> начала и конца подстроки, записанной на данном переходе. Итак, дерево занимает <tex>O(n|\Sigma|)</tex> памяти. |
==Построение суффиксного дерева== | ==Построение суффиксного дерева== | ||
| Строка 46: | Строка 70: | ||
===Наивный алгоритм=== | ===Наивный алгоритм=== | ||
Рассмотрим наивный алгоритм построения суффиксного дерева строки <tex>s</tex>: | Рассмотрим наивный алгоритм построения суффиксного дерева строки <tex>s</tex>: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | insert(l, r): | + | '''struct''' Vertex: <span style="color:Green">// Структура, содержащая информацию о вершине </span> |
| + | '''int''' l <span style="color:Green">// индекс начала подстроки </span> | ||
| + | '''int''' r <span style="color:Green">// индекс конца подстроки </span> | ||
| + | '''int''' v <span style="color:Green">// индекс текущей позиции </span> | ||
| + | |||
| + | go[0] = '''new''' Vertex <span style="color:Green">// массив из пустых Vertex (можно все поля положить -1), размер массива -- количество символов в алфавите </span> | ||
| + | count = 0 <span style="color:Green">// номер последней вершины, созданной в дереве (глобальная переменная)</span> | ||
| + | '''for''' i = 0 '''to''' n <span style="color:Green">// для каждого символа строки</span> | ||
| + | insert(i, n) <span style="color:Green">// добавляем суффикс, начинающийся с него</span> | ||
| + | |||
| + | '''void''' insert('''int''' l, '''int''' r): | ||
cur = 0 | cur = 0 | ||
| − | '''while''' l < r | + | '''while''' (l < r) |
| − | '''if''' go[cur][s[l]].v == -1 | + | '''if''' (go[cur][s[l]].v == -1) <span style="color:Green">// если мы не можем пойти из вершины по символу <tex> l </tex></span> |
| − | createVertex(cur, l, r) | + | createVertex(cur, l, r) <span style="color:Green">// создаем новую вершину</span> |
'''else''' | '''else''' | ||
start = go[cur][s[l]].l | start = go[cur][s[l]].l | ||
finish = go[cur][s[l]].r | finish = go[cur][s[l]].r | ||
| − | hasCut = false | + | hasCut = ''false'' |
| − | '''for''' j = start '''to''' finish | + | '''for''' j = start '''to''' finish and l + j - start < n <span style="color:Green">// для каждого символа на ребре из текущей вершины</span> |
| − | '''if''' s[l+j-start] | + | '''if''' (s[l + j - start] != s[j]) <span style="color:Green">// если нашли не совпадающий символ</span> |
| − | // создаем вершину на ребре | + | <span style="color:Green">// создаем вершину на ребре</span> |
old = go[cur][s[l]] | old = go[cur][s[l]] | ||
| − | createVertex(cur, l, j | + | createVertex(cur, l, j) |
go[count][s[j]].v = old | go[count][s[j]].v = old | ||
| − | go[count][s[j]]. | + | go[count][s[j]].l = j |
| − | go[count][s[j]]. | + | go[count][s[j]].r = finish |
createVertex(count, l + j - start, r) | createVertex(count, l + j - start, r) | ||
| − | hasCut = true | + | hasCut = ''true'' |
'''break''' | '''break''' | ||
| − | '''if''' !hasCut | + | '''if''' (!hasCut) |
| − | cur = go[cur][s[l]].v // переходим по ребру | + | cur = go[cur][s[l]].v <span style="color:Green">// переходим по ребру</span> |
| − | l = l + finish - start // двигаемся по суффиксу на длину подстроки, записанной на ребре | + | l = l + finish - start <span style="color:Green">// двигаемся по суффиксу на длину подстроки, записанной на ребре</span> |
'''else''' | '''else''' | ||
'''break''' | '''break''' | ||
| − | createVertex(cur, l, r): | + | '''void''' createVertex('''int''' cur, '''int''' l, '''int''' r): |
| − | go[++count] = Vertex | + | go[++count] = '''new''' Vertex |
go[cur][s[l]].v = count | go[cur][s[l]].v = count | ||
go[cur][s[l]].l = l | go[cur][s[l]].l = l | ||
go[cur][s[l]].r = r | go[cur][s[l]].r = r | ||
| − | |||
Этот алгоритм работает за время <tex>O(n^2)</tex>, однако [[Алгоритм Укконена| алгоритм Укконена]] позволяет построить сжатое суффиксное дерево за <tex>O(n)</tex>. | Этот алгоритм работает за время <tex>O(n^2)</tex>, однако [[Алгоритм Укконена| алгоритм Укконена]] позволяет построить сжатое суффиксное дерево за <tex>O(n)</tex>. | ||
===Построение из суффиксного массива=== | ===Построение из суффиксного массива=== | ||
| − | Пусть нам известен [[Суффиксный массив| суффиксный массив]] <tex>suf</tex> строки <tex>s</tex>, его можно получить [[Алгоритм Карккайнена-Сандерса| алгоритмом Карккайнена-Сандерса]] за линейное время. Для преобразования нам также понадобится массив <tex>lcp</tex> (longest common prefix), который можно получить [[Алгоритм Касаи и др.| алгоритмом Касаи]]. | + | Пусть нам известен [[Суффиксный массив| суффиксный массив]] <tex>suf</tex> строки <tex>s</tex>, его можно получить [[Алгоритм Карккайнена-Сандерса| алгоритмом Карккайнена-Сандерса]] за линейное время. Для преобразования нам также понадобится массив <tex>lcp</tex> (''longest common prefix''), который можно получить [[Алгоритм Касаи и др.| алгоритмом Касаи]]. |
В этом преобразовании используется тот же инвариант, что и в других суффиксных структурах: | В этом преобразовании используется тот же инвариант, что и в других суффиксных структурах: | ||
| Строка 94: | Строка 123: | ||
Будем строить дерево, добавляя суффиксы в лексикографическом порядке. Чтобы ускорить добавление, будем использовать то, что <tex>i</tex>-ый суффикс имеет с предыдущим <tex>lcp[i]</tex> общих символов. Тогда добавление из корня не отличается от того, что мы поднимемся вверх из предыдущего суффикса до глубины <tex>lcp[i]</tex> и продолжим построение оттуда. Инвариант позволяет нам утверждать, что ни один лист мы не сможем продолжить, и нам всегда нужно будет хоть раз подняться из него вверх. Поскольку суффиксы отсортированы лексикографически, мы не будем спускаться по ребру после того, как уже поднялись из него из-за несовпадения символа. Все это позволяет сформулировать алгоритм добавления суффикса по известной вершине предыдущего суффикса: | Будем строить дерево, добавляя суффиксы в лексикографическом порядке. Чтобы ускорить добавление, будем использовать то, что <tex>i</tex>-ый суффикс имеет с предыдущим <tex>lcp[i]</tex> общих символов. Тогда добавление из корня не отличается от того, что мы поднимемся вверх из предыдущего суффикса до глубины <tex>lcp[i]</tex> и продолжим построение оттуда. Инвариант позволяет нам утверждать, что ни один лист мы не сможем продолжить, и нам всегда нужно будет хоть раз подняться из него вверх. Поскольку суффиксы отсортированы лексикографически, мы не будем спускаться по ребру после того, как уже поднялись из него из-за несовпадения символа. Все это позволяет сформулировать алгоритм добавления суффикса по известной вершине предыдущего суффикса: | ||
| − | # Подняться из вершины вверх до глубины <tex>lcp</tex> | + | # Подняться из вершины вверх до глубины <tex>lcp</tex>. |
# Если эта глубина находится на ребре, разрезать ребро по ней. | # Если эта глубина находится на ребре, разрезать ребро по ней. | ||
| − | # Вставить новую вершину как сына вершины с глубиной <tex>lcp</tex> | + | # Вставить новую вершину как сына вершины с глубиной <tex>lcp</tex>. |
| − | В вершинах дерева <tex>Node</tex> мы будем хранить предка <tex>parent</tex>, [[Стек| стек]] детей в лексикографическом порядке ребер <tex>children</tex>, глубину вершины в символах от корня <tex>depth</tex>. | + | В вершинах дерева <tex>Node</tex> мы будем хранить предка <tex>\mathtt {parent}</tex>, [[Стек| стек]] детей в лексикографическом порядке ребер <tex>\mathtt{children}</tex>, глубину вершины в символах от корня <tex>\mathtt{depth}</tex>. |
Соответственно, конструктор вершины имеет вид <code>Node(Node parent, '''int''' depth)</code>. | Соответственно, конструктор вершины имеет вид <code>Node(Node parent, '''int''' depth)</code>. | ||
<code> | <code> | ||
| − | Node addNextSuffix(Node previous, '''int''' length, '''int''' lcp): | + | '''Node''' addNextSuffix('''Node''' previous, '''int''' length, '''int''' lcp): |
| − | '''if''' previous.depth == 0 '''or''' previous.depth == lcp | + | '''if''' (previous.depth == 0 '''or''' previous.depth == lcp) <font color=green> // Добавляем к сыновьям текущей вершины </font> |
| − | added = Node(previous, length) | + | added = '''Node'''(previous, length) |
previous.children.push(added) | previous.children.push(added) | ||
'''return''' added | '''return''' added | ||
'''else''' | '''else''' | ||
| − | '''if''' previous.parent.depth < lcp | + | '''if''' previous.parent.depth < lcp <font color=green> // Нужно разрезать ребро </font> |
| − | inserted = Node(prevous.parent, lcp) | + | inserted = '''Node'''(prevous.parent, lcp) |
previous.parent.children.pop() | previous.parent.children.pop() | ||
previous.parent.children.push(inserted) | previous.parent.children.push(inserted) | ||
| Строка 116: | Строка 145: | ||
'''return''' addNextSuffix(previous.parent, length, lcp) | '''return''' addNextSuffix(previous.parent, length, lcp) | ||
| − | Node buildSuffixTree('''int[]''' suf, '''int[]''' lcp, '''int''' length): | + | '''Node''' buildSuffixTree('''int[]''' suf, '''int[]''' lcp, '''int''' length): |
| − | root = Node('''null''', 0) | + | root = '''Node'''('''null''', 0) |
previous = root | previous = root | ||
'''for''' i = 1 '''to''' length | '''for''' i = 1 '''to''' length | ||
| Строка 124: | Строка 153: | ||
</code> | </code> | ||
| − | В процессе построения мы нигде не запоминали сами позиции строки, соответствующие ребрам. Чтобы их восстановить, достаточно определить максимальный суффикс, который проходит по этому ребру. Для этого с помощью [[Обход в глубину, цвета вершин| обхода в глубину]] посчитаем для каждой вершину дерева максимальную глубину ее листа <tex>maxDepth</tex>. | + | В процессе построения мы нигде не запоминали сами позиции строки, соответствующие ребрам. Чтобы их восстановить, достаточно определить максимальный суффикс, который проходит по этому ребру. Для этого с помощью [[Обход в глубину, цвета вершин| обхода в глубину]] посчитаем для каждой вершину дерева максимальную глубину ее листа <tex>\mathtt{maxDepth}</tex>. |
Тогда ребро <tex>s[start, end]</tex> определяется так: | Тогда ребро <tex>s[start, end]</tex> определяется так: | ||
<code> | <code> | ||
| − | ''' | + | '''void''' calculatePositions('''Node''' parent, '''Node''' child, '''int''' stringLength): |
start = stringLength - child.maxDepth + parent.depth | start = stringLength - child.maxDepth + parent.depth | ||
end = start + child.depth - parent.depth - 1 | end = start + child.depth - parent.depth - 1 | ||
| Строка 138: | Строка 167: | ||
==Использование сжатого суффиксного дерева== | ==Использование сжатого суффиксного дерева== | ||
Суффиксное дерево позволяет за линейное время найти: | Суффиксное дерево позволяет за линейное время найти: | ||
| − | + | # Количество различных подстрок данной строки. | |
| − | + | # Наибольшую общую подстроку двух строк. | |
| − | + | # [[Суффиксный массив| Суффиксный массив]] и массив <tex>lcp</tex> (''longest common prefix'') исходной строки. | |
| − | + | # Строку максимальной длины, ветвящуюся влево и вправо за <tex>ST + O(n)</tex>. | |
===Построение суффиксного массива и массива lcp из суффиксного дерева=== | ===Построение суффиксного массива и массива lcp из суффиксного дерева=== | ||
| Строка 150: | Строка 179: | ||
Тогда суффиксный массив строится из суффиксного дерева [[Обход в глубину, цвета вершин| обходом в глубину]] в указанном порядке. | Тогда суффиксный массив строится из суффиксного дерева [[Обход в глубину, цвета вершин| обходом в глубину]] в указанном порядке. | ||
| − | Пусть длина строки <tex>length</tex>, глубина листа в символах <tex>depth</tex>, тогда номер суффикса <tex>i = length - depth</tex>. | + | Пусть длина строки <tex>\mathtt{length}</tex>, глубина листа в символах <tex>\mathtt{depth}</tex>, тогда номер суффикса <tex>\mathtt{i = length - depth}</tex>. |
| − | Для заполнения массива <tex>lcp</tex> нам понадобится вершина <tex>minNode</tex>, которая будет означать вершину с минимальной глубиной, в которую мы поднимались при переходе между суффиксами. Поскольку мы точно поднимались туда, но не поднимались выше, это будет [[Сведение задачи LCA к задаче RMQ| наименьший общий предок]] этих узлов. Из этого следует, что у рассматриваемых суффиксов совпадает ровно <tex>lcp = minNode.depth</tex> символов. | + | Для заполнения массива <tex>lcp</tex> нам понадобится вершина <tex>\mathtt{minNode}</tex>, которая будет означать вершину с минимальной глубиной, в которую мы поднимались при переходе между суффиксами. Поскольку мы точно поднимались туда, но не поднимались выше, это будет [[Сведение задачи LCA к задаче RMQ| наименьший общий предок]] этих узлов. Из этого следует, что у рассматриваемых суффиксов совпадает ровно <tex>\mathtt{lcp = minNode.depth}</tex> символов. |
<code> | <code> | ||
'''int''' curPos = 0 | '''int''' curPos = 0 | ||
| − | Node minNode = root | + | '''Node''' minNode = root |
<font color=green>// Для заполнения нужно вызвать dfs(root) </font> | <font color=green>// Для заполнения нужно вызвать dfs(root) </font> | ||
| − | ''' | + | '''void''' dfs('''Node''' n): |
'''if''' n.children.size == 0 | '''if''' n.children.size == 0 | ||
suf[curPos] = length - n.depth | suf[curPos] = length - n.depth | ||
| Строка 191: | Строка 220: | ||
'''Вершина <tex>v</tex> различна влево''', если как минимум два листа в поддереве <tex>v</tex> имеют различные ''левые символы''. По определению лист не может быть различным влево. | '''Вершина <tex>v</tex> различна влево''', если как минимум два листа в поддереве <tex>v</tex> имеют различные ''левые символы''. По определению лист не может быть различным влево. | ||
}} | }} | ||
| + | [[Файл:LeftBranchingSS.png|thumb|400px|right|Левые вершины и символы для суффиксного дерева над строкой <tex>aabcabd</tex> (символом <tex>\#</tex> помечены различные влево вершины)]] | ||
| + | Допустим, что строка ветвится влево. Пусть существуют подстроки <tex>cs</tex> и <tex>ds</tex>, тогда есть два суффикса, начинающиеся с <tex>s</tex>, которым соответствуют различные листовые вершины с различными левыми символами (<tex>c</tex> и <tex>d</tex>). Также в дереве существует внутренняя вершина <tex>v</tex>, соответствующая строке <tex>s</tex>. Из определения следует, что <tex>v</tex> различна влево. | ||
| + | |||
| + | Чтобы найти строки, ветвящиеся влево, нужно проверить все внутренние вершины суффиксного дерева на различность влево. Если какая-то вершина <tex>v</tex> будет различна влево и удовлетворять свойству ветвимости право, то строка, соответствующая вершине <tex>v</tex> будет ветвится вправо и влево. | ||
| + | |||
| + | Чтобы найти вершины различные влево, нужно хранить левый символ для каждой вершины или информацию о том, что она различна влево. Для поиска строки, ветвящейся влево, нужно промаркировать всё дерево. Сделать это можно при помощи [[Обход в глубину, цвета вершин| обхода в глубину]]. Начиная с корня, спускаясь вниз, для листов левый символ уже известен {{---}} при добавление нового суффикса в дерево записываем левый символ для него в лист, для вершины <tex>v</tex> запустим проверку. | ||
| + | |||
| + | :'''Случай 1.''' Если среди левых детей <tex>v</tex> есть хотя бы один, удовлетворяющий свойству различности влево, то обозначаем <tex>v</tex> как различную влево вершину (в суффиксном дереве свойство различности влево передаётся от детей к родителю {{---}} строка соответствующая вершине <tex>v</tex> и строка соответствующая ребёнку <tex>v</tex> начинаются с одного и того же символа). | ||
| − | + | :'''Случай 2.''' Если среди левых символов детей <tex>v</tex> нет ни одного со свойством различная влево вершина, то проверяем на совпадение левые символы детей. | |
| − | + | ::'''Случай 2.1.''' Если все левые символ детей <tex>v</tex> одинаковы и эквивалентны <tex>x</tex>, то записываем в <tex>v</tex> этот символ <tex>x</tex>. | |
| − | + | ::'''Случай 2.2.''' Если не все левые символы детей <tex>v</tex> эквивалентны, то записываем в <tex>v</tex>, что она различна влево. | |
| − | |||
| − | |||
| − | |||
| − | |||
Так как время проверки <tex>v</tex> пропорционально числу детей, время работы всего алгоритма {{---}} <tex>O(n)</tex>. | Так как время проверки <tex>v</tex> пропорционально числу детей, время работы всего алгоритма {{---}} <tex>O(n)</tex>. | ||
| − | + | Теперь несложно среди всех найденных строк найти строку максимальной длины (также этот алгоритм можно использовать для нахождения количества строк, ветвящихся влево и вправо). | |
| − | Таким образом можно найти строку максимальной длины, ветвящуюся влево и вправо за <tex>ST+O(n)</tex>, где <tex>ST</tex> {{---}} время построения суффиксного дерева. | + | Таким образом можно найти строку максимальной длины, ветвящуюся влево и вправо, за время <tex>ST+O(n)</tex>, где <tex>ST</tex> {{---}} время построения суффиксного дерева. |
==См. также== | ==См. также== | ||
Текущая версия на 19:41, 4 сентября 2022
Суффиксный бор — удобная структура данных для поиска подстроки в строке, но она требует порядка квадрата длины исходной строки памяти. Оптимизацией суффиксного бора, требующей линейное количество памяти, является сжатое суффиксное дерево (англ. compressed suffix tree), рассматриваемое далее.
Содержание
Определение
- каждая внутренняя вершина дерева имеет не меньше двух детей;
- каждое ребро помечено непустой подстрокой строки ;
- никакие два ребра, выходящие из одной вершины, не могут иметь пометок, начинающихся с одного и того же символа;
- дерево должно содержать все суффиксы строки , причем каждый суффикс заканчивается точно в листе и нигде кроме него.
Данное определение порождает следующую проблему:
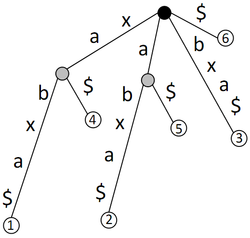
Рассмотрим дерево для строки : суффикс является префиксом суффикса , а, значит, этот суффикс не закачивается в листе. Для решения проблемы в конце строки добавляют символ, не входящий в исходный алфавит: защитный символ. Обозначим его как . Любой суффикс строки с защитным символом действительно заканчивается в листе и только в листе, т. к. в такой строке не существует двух различных подстрок одинаковой длины, заканчивающихся на .
Далее — длина строки с защитным символом.
Число вершин
По определению, в суффиксном дереве содержится листьев. Оценим число внутренних вершин такого дерева.
| Лемма: |
Число внутренних вершин дерева, каждая из которых имеет не менее двух детей, меньше числа листьев. |
| Доказательство: |
|
Занимаемая память
Представим дерево как двумерный массив размера , где — число вершин в дереве, — мощность алфавита. Для любого суффиксного дерева верна предыдущая лемма (у каждой вершины, по определению, не менее двух детей), значит, . Каждая ячейка содержит информацию о том, в какую вершину ведет ребро из -ой вершины по -ому символу и индексы начала и конца подстроки, записанной на данном переходе. Итак, дерево занимает памяти.
Построение суффиксного дерева
Наивный алгоритм
Рассмотрим наивный алгоритм построения суффиксного дерева строки :
struct Vertex: // Структура, содержащая информацию о вершине int l // индекс начала подстроки int r // индекс конца подстроки int v // индекс текущей позиции go[0] = new Vertex // массив из пустых Vertex (можно все поля положить -1), размер массива -- количество символов в алфавите count = 0 // номер последней вершины, созданной в дереве (глобальная переменная) for i = 0 to n // для каждого символа строки insert(i, n) // добавляем суффикс, начинающийся с него
void insert(int l, int r):
cur = 0
while (l < r)
if (go[cur][s[l]].v == -1) // если мы не можем пойти из вершины по символу
createVertex(cur, l, r) // создаем новую вершину
else
start = go[cur][s[l]].l
finish = go[cur][s[l]].r
hasCut = false
for j = start to finish and l + j - start < n // для каждого символа на ребре из текущей вершины
if (s[l + j - start] != s[j]) // если нашли не совпадающий символ
// создаем вершину на ребре
old = go[cur][s[l]]
createVertex(cur, l, j)
go[count][s[j]].v = old
go[count][s[j]].l = j
go[count][s[j]].r = finish
createVertex(count, l + j - start, r)
hasCut = true
break
if (!hasCut)
cur = go[cur][s[l]].v // переходим по ребру
l = l + finish - start // двигаемся по суффиксу на длину подстроки, записанной на ребре
else
break
void createVertex(int cur, int l, int r):
go[++count] = new Vertex
go[cur][s[l]].v = count
go[cur][s[l]].l = l
go[cur][s[l]].r = r
Этот алгоритм работает за время , однако алгоритм Укконена позволяет построить сжатое суффиксное дерево за .
Построение из суффиксного массива
Пусть нам известен суффиксный массив строки , его можно получить алгоритмом Карккайнена-Сандерса за линейное время. Для преобразования нам также понадобится массив (longest common prefix), который можно получить алгоритмом Касаи.
В этом преобразовании используется тот же инвариант, что и в других суффиксных структурах:
- Строка заканчивается специальным символом, который больше не встречается в строке.
- Следствие: , где — длина суффикса, соответствующего .
Будем строить дерево, добавляя суффиксы в лексикографическом порядке. Чтобы ускорить добавление, будем использовать то, что -ый суффикс имеет с предыдущим общих символов. Тогда добавление из корня не отличается от того, что мы поднимемся вверх из предыдущего суффикса до глубины и продолжим построение оттуда. Инвариант позволяет нам утверждать, что ни один лист мы не сможем продолжить, и нам всегда нужно будет хоть раз подняться из него вверх. Поскольку суффиксы отсортированы лексикографически, мы не будем спускаться по ребру после того, как уже поднялись из него из-за несовпадения символа. Все это позволяет сформулировать алгоритм добавления суффикса по известной вершине предыдущего суффикса:
- Подняться из вершины вверх до глубины .
- Если эта глубина находится на ребре, разрезать ребро по ней.
- Вставить новую вершину как сына вершины с глубиной .
В вершинах дерева мы будем хранить предка , стек детей в лексикографическом порядке ребер , глубину вершины в символах от корня .
Соответственно, конструктор вершины имеет вид Node(Node parent, int depth).
Node addNextSuffix(Node previous, int length, int lcp):
if (previous.depth == 0 or previous.depth == lcp) // Добавляем к сыновьям текущей вершины
added = Node(previous, length)
previous.children.push(added)
return added
else
if previous.parent.depth < lcp // Нужно разрезать ребро
inserted = Node(prevous.parent, lcp)
previous.parent.children.pop()
previous.parent.children.push(inserted)
inserted.children.push(previous)
previous.parent = inserted
return addNextSuffix(previous.parent, length, lcp)
Node buildSuffixTree(int[] suf, int[] lcp, int length):
root = Node(null, 0)
previous = root
for i = 1 to length
previous = addNextSuffix(previous, length - suf[i], lcp[i])
return root
В процессе построения мы нигде не запоминали сами позиции строки, соответствующие ребрам. Чтобы их восстановить, достаточно определить максимальный суффикс, который проходит по этому ребру. Для этого с помощью обхода в глубину посчитаем для каждой вершину дерева максимальную глубину ее листа .
Тогда ребро определяется так:
void calculatePositions(Node parent, Node child, int stringLength): start = stringLength - child.maxDepth + parent.depth end = start + child.depth - parent.depth - 1
Для асимптотического анализа будем использовать в качестве потенциала глубину в вершинах. При добавлении суффикса мы спускаемся один раз, подняться выше корня мы не можем, значит, и подниматься мы будем суммарно раз. Обход в глубину также выполняется за , итоговая асимптотика .
Использование сжатого суффиксного дерева
Суффиксное дерево позволяет за линейное время найти:
- Количество различных подстрок данной строки.
- Наибольшую общую подстроку двух строк.
- Суффиксный массив и массив (longest common prefix) исходной строки.
- Строку максимальной длины, ветвящуюся влево и вправо за .
Построение суффиксного массива и массива lcp из суффиксного дерева
Пусть к строке дописан специальный символ для сохранения инварианта. Рассмотрим лексикографический по ребрам порядок обхода сжатого суффиксного дерева. Пусть два суффикса имеют общее начало, но различаются в -ом символе. Первым будет рассмотрено поддерево по ребру с меньшим символом, значит и лист, соответствующий этому суффиксу, будет посещен первым.
Тогда суффиксный массив строится из суффиксного дерева обходом в глубину в указанном порядке. Пусть длина строки , глубина листа в символах , тогда номер суффикса .
Для заполнения массива нам понадобится вершина , которая будет означать вершину с минимальной глубиной, в которую мы поднимались при переходе между суффиксами. Поскольку мы точно поднимались туда, но не поднимались выше, это будет наименьший общий предок этих узлов. Из этого следует, что у рассматриваемых суффиксов совпадает ровно символов.
int curPos = 0
Node minNode = root
// Для заполнения нужно вызвать dfs(root)
void dfs(Node n):
if n.children.size == 0
suf[curPos] = length - n.depth
lcp[curPos] = minNode.depth
curPos++
minNode = n
else
foreach child in n.children
if n.depth < minNode.depth:
minNode = n
dfs(child)
Асимптотика алгоритма совпадает с асимптотикой обхода в глубину и составляет .
Таким образом, мы умеем за строить суффиксное дерево, суффиксный массив и преобразовывать одно в другое.
Поиск строки максимальной длины, ветвящейся влево и вправо
| Определение: |
| Строка называется ветвящейся вправо в (англ. right branching string), если существуют символы и , такие что : и — подстроки . Аналогично, ветвящаяся влево (англ. left branching), если и — подстроки . |
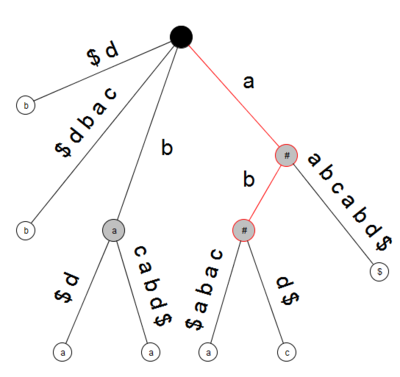
Построим cуффиксное дерево при помощи алгоритма Укконена. В полученном дереве не листовой вершине будет соответствовать подстрока , которая ветвится вправо, при условии, что количество "хороших" детей вершины ("хорошие" дети — листы, метка которых ). В примере для строки это , и . Далее введём термины левый символ и вершина различная влево, чтобы найти строки, ветвящиеся влево.
| Определение: |
| Левый символ для позиции строки — это символ . Левым символом листа называется левый символ начала суффикса, ведущего в этот лист. |
| Определение: |
| Вершина различна влево, если как минимум два листа в поддереве имеют различные левые символы. По определению лист не может быть различным влево. |
Допустим, что строка ветвится влево. Пусть существуют подстроки и , тогда есть два суффикса, начинающиеся с , которым соответствуют различные листовые вершины с различными левыми символами ( и ). Также в дереве существует внутренняя вершина , соответствующая строке . Из определения следует, что различна влево.
Чтобы найти строки, ветвящиеся влево, нужно проверить все внутренние вершины суффиксного дерева на различность влево. Если какая-то вершина будет различна влево и удовлетворять свойству ветвимости право, то строка, соответствующая вершине будет ветвится вправо и влево.
Чтобы найти вершины различные влево, нужно хранить левый символ для каждой вершины или информацию о том, что она различна влево. Для поиска строки, ветвящейся влево, нужно промаркировать всё дерево. Сделать это можно при помощи обхода в глубину. Начиная с корня, спускаясь вниз, для листов левый символ уже известен — при добавление нового суффикса в дерево записываем левый символ для него в лист, для вершины запустим проверку.
- Случай 1. Если среди левых детей есть хотя бы один, удовлетворяющий свойству различности влево, то обозначаем как различную влево вершину (в суффиксном дереве свойство различности влево передаётся от детей к родителю — строка соответствующая вершине и строка соответствующая ребёнку начинаются с одного и того же символа).
- Случай 2. Если среди левых символов детей нет ни одного со свойством различная влево вершина, то проверяем на совпадение левые символы детей.
- Случай 2.1. Если все левые символ детей одинаковы и эквивалентны , то записываем в этот символ .
- Случай 2.2. Если не все левые символы детей эквивалентны, то записываем в , что она различна влево.
Так как время проверки пропорционально числу детей, время работы всего алгоритма — .
Теперь несложно среди всех найденных строк найти строку максимальной длины (также этот алгоритм можно использовать для нахождения количества строк, ветвящихся влево и вправо).
Таким образом можно найти строку максимальной длины, ветвящуюся влево и вправо, за время , где — время построения суффиксного дерева.
См. также
Источники информации
- Дэн Гасфилд — Строки, деревья и последовательности в алгоритмах: Информатика и вычислительная биология — СПб.: Невский Диалект; БХВ-Петербург, 2003. — 654 с: ил.