Хроматическое число планарного графа — различия между версиями
Martoon (обсуждение | вклад) м |
м (rollbackEdits.php mass rollback) |
||
| (не показано 38 промежуточных версий 7 участников) | |||
| Строка 4: | Строка 4: | ||
{{Лемма | {{Лемма | ||
|id=5deg_vertex_lemma | |id=5deg_vertex_lemma | ||
| − | |statement=В любом графе <tex> G </tex> существует вершина [[Основные определения теории графов#def_undirected_graph_2 | степени]] не больше 5. | + | |statement=В любом планарном графе <tex> G </tex> существует вершина [[Основные определения теории графов#def_undirected_graph_2 | степени]] не больше <tex>5</tex>. |
|proof= | |proof= | ||
| − | Предположим это не так. Для любой вершины <tex> u_i </tex> графа <tex> G </tex> верно <tex> \mathrm{deg} \; u_i \ | + | Предположим это не так. Для любой вершины <tex> u_i </tex> графа <tex> G </tex> верно <tex> \mathrm{deg} \; u_i \geqslant 6 </tex>. Если сложить это неравенство для всех <tex> i </tex>, получим <tex> 2E \geqslant 6V </tex>. Но по [[Формула_Эйлера#EulerFormulaCons|следствию из теоремы Эйлера]] <tex> E \leqslant 3V-6 </tex>. Пришли к противоречию. |
}} | }} | ||
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
| − | Пусть граф <tex>G</tex> | + | Пусть граф <tex>G</tex> — планарный. Тогда <tex> \chi (G) \leqslant 6.</tex> |
|proof= | |proof= | ||
Докажем по индукции. | Докажем по индукции. | ||
| − | + | ||
| − | + | <u>'''''База индукции'''''</u> | |
| − | + | ||
| − | + | Если граф содержит не более <tex>6</tex> вершин, то очевидно, что <tex> \chi (G) \leqslant 6.</tex> | |
| − | + | ||
| − | + | <u>'''''Индукционный переход'''''</u> | |
| + | |||
| + | Предположим, что для планарного графа с <tex>N</tex> вершинами существует раскраска в <tex>6</tex> цветов. Докажем то же для графа с <tex> N+1 </tex> вершиной. | ||
| + | |||
| + | По только что доказанной лемме в <tex> G </tex> найдётся вершина степени не больше <tex>5</tex>. Удалим её; по предположению индукции получившийся граф можно раскрасить в <tex>6</tex> цветов. | ||
| + | |||
| + | Вернём удалённую вершину и покрасим её в цвет, не встречающийся среди смежных ей вершин (ведь "занято" максимум <tex>5</tex> цветов). Индукционный переход доказан. | ||
}} | }} | ||
== Раскраска в 5 цветов == | == Раскраска в 5 цветов == | ||
| − | {{Теорема | + | {{Теорема |
| + | |about= | ||
| + | Хивуд | ||
|statement= | |statement= | ||
| − | Пусть граф <tex>G</tex> | + | Пусть граф <tex>G</tex> — планарный. Тогда <tex> \chi (G) \leqslant 5.</tex> |
|proof= | |proof= | ||
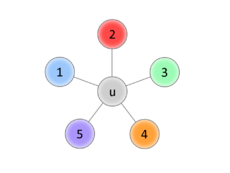
| − | [[Файл:Planar chromatic number 1.png|230px|thumb|right|u и смежные ей вершины]] | + | [[Файл:Planar chromatic number 1.png|230px|thumb|right|<tex>u</tex> и смежные ей вершины]] |
| − | Начало доказательства такое же, как в предыдущей теореме, трудность возникает в индукционном переходе. Покажем что для случая с 5-ю цветами всё равно можно вернуть удалённую вершину так, чтобы раскраска осталась правильной. | + | Начало доказательства такое же, как в предыдущей теореме, трудность возникает в индукционном переходе. Покажем что для случая с <tex>5</tex>-ю цветами всё равно можно вернуть удалённую вершину так, чтобы раскраска осталась правильной. |
| − | Обозначим за <tex> u </tex> | + | Обозначим за <tex> u </tex> — возвращаемую вершину, <tex> v^{(k)} </tex> — вершину, покрашенную в <tex> k </tex> цвет. |
Если среди вершин, смежных <tex> u </tex>, есть две вершины одного цвета, значит остаётся по меньшей мере один свободный цвет, в который мы и покрасим <tex> u </tex>. | Если среди вершин, смежных <tex> u </tex>, есть две вершины одного цвета, значит остаётся по меньшей мере один свободный цвет, в который мы и покрасим <tex> u </tex>. | ||
| Строка 36: | Строка 44: | ||
Иначе, уложим полученный после удаления <tex> u </tex> граф на плоскость, вернём вершину <tex> u </tex> (пока бесцветную) и пронумеруем цвета в порядке обхода смежных вершин по часовой стрелке. | Иначе, уложим полученный после удаления <tex> u </tex> граф на плоскость, вернём вершину <tex> u </tex> (пока бесцветную) и пронумеруем цвета в порядке обхода смежных вершин по часовой стрелке. | ||
| − | Попробуем покрасить <tex> u </tex> в цвет 1. Чтобы раскраска осталась правильной, перекрасим смежную ей вершину <tex>v_1^{(1)}</tex> в цвет 3. Если среди смежных ей вершин есть вершины <tex> v_i^{(3)} </tex>, покрасим их в цвет 1, и так далее. Рассмотрим две необычные ситуации, которые могут наступить во время обхода: | + | Попробуем покрасить <tex> u </tex> в цвет <tex>1</tex>. Чтобы раскраска осталась правильной, перекрасим смежную ей вершину <tex>v_1^{(1)}</tex> в цвет <tex>3</tex>. Если среди смежных ей вершин есть вершины <tex> v_i^{(3)} </tex>, покрасим их в цвет <tex>1</tex>, и так далее. Рассмотрим две необычные ситуации, которые могут наступить во время обхода: |
| − | #мы дойдём до уже однажды перекрашенной вершины (и хотим перекрасить её обратно, что не получится сделать). Видно что такая ситуация невозможна, поскольку мы меняли цвета вершин по схеме 1 <tex>\leftrightarrow</tex> 3, и если по завершении обхода мы получили две смежные вершины одного цвета, значит и до перекрасок в этом месте были две вершины одинакового цвета, а по предположению граф без <tex> u </tex> был раскрашен правильно. | + | #мы дойдём до уже однажды перекрашенной вершины (и хотим перекрасить её обратно, что не получится сделать). Видно что такая ситуация невозможна, поскольку мы меняли цвета вершин по схеме <tex>1</tex> <tex>\leftrightarrow</tex> <tex>3</tex>, и если по завершении обхода мы получили две смежные вершины одного цвета, значит и до перекрасок в этом месте были две вершины одинакового цвета, а по предположению граф без <tex> u </tex> был раскрашен правильно. |
| − | #дойдём до вершины, смежной <tex> u </tex>, исходно имевшей цвет 3, которую перекрасить в 1 нельзя (<tex> u </tex> теперь имеет цвет 1). | + | #дойдём до вершины, смежной <tex> u </tex>, исходно имевшей цвет <tex>3</tex>, которую перекрасить в <tex>1</tex> нельзя (<tex> u </tex> теперь имеет цвет <tex>1</tex>). |
Если этот процесс был успешно завершён, то получили правильную раскраску. | Если этот процесс был успешно завершён, то получили правильную раскраску. | ||
| − | Если же в соответствии со | + | Если же в соответствии со вторым вариантом перекраска не удалась, это означает, что в графе есть цикл <tex> u v_1^{(1)} v_2^{(3)} v_3^{(1)} \ldots v_{k-1}^{(1)} v_k^{(3)} u </tex>. |
| − | Тогда попытаемся таким же образом перекрасить <tex> u </tex> в цвет 2, а смежную ей <tex>w_1^{(2)}</tex> в цвет 4 (со последующими перекрасками). Если удастся | + | Тогда попытаемся таким же образом перекрасить <tex> u </tex> в цвет <tex>2</tex>, а смежную ей <tex>w_1^{(2)}</tex> в цвет <tex>4</tex> (со последующими перекрасками). Если удастся — раскраска получена. |
| − | Если нет, то получили ещё один цикл <tex> u w_1^{(2)} w_2^{(4)} w_3^{(2)} ... w_{k-1}^{(2)} w_k^{(4)} u </tex>. Но граф планарный, значит два полученных цикла пересекаются помимо вершины <tex> u </tex> по крайней мере ещё в одной, что невозможно, ведь вершины <tex> v_i </tex> первого цикла и <tex> w_j </tex> второго | + | Если нет, то получили ещё один цикл <tex> u w_1^{(2)} w_2^{(4)} w_3^{(2)} ... w_{k-1}^{(2)} w_k^{(4)} u </tex>. Но граф планарный, значит два полученных цикла пересекаются помимо вершины <tex> u </tex> по крайней мере ещё в одной, что невозможно, ведь вершины <tex> v_i </tex> первого цикла и <tex> w_j </tex> второго — разных цветов. Значит такой случай наступить не мог. |
}} | }} | ||
{| cellpadding="10" | {| cellpadding="10" | ||
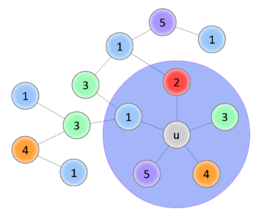
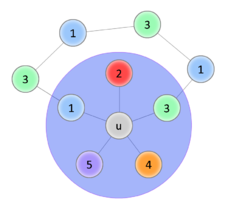
| − | | Успешное перекрашивание || || || || || || Цикл | + | | || || || || Успешное перекрашивание || || || || || || Цикл 1—3, перекрасить не удаётся || |
| + | |- | ||
| + | | || || || || [[Файл:Planar chromatic number 2.png|264px]] || || || || || || [[Файл:Planar chromatic number 4.png|228px]] | ||
|- | |- | ||
| − | | | + | | || || || || [[Файл:Planar chromatic number 3.png|264px]] || || || || || || [[Файл:Planar chromatic number 5.png|228px]] |
|} | |} | ||
| − | Заметим что не удаётся составить подобное доказательство для раскраски в | + | Заметим, что не удаётся составить подобное доказательство для раскраски в четыре цвета, поскольку здесь наличие двух вершин одного цвета среди смежных <tex> u </tex> не исключает того, что при их (смежных вершин) раскраске использовались все возможные цвета. |
== Раскраска в 4 цвета == | == Раскраска в 4 цвета == | ||
| − | + | {{Теорема | |
| + | |about= | ||
| + | Проблема четырех красок | ||
| + | |statement='''Теорема о четырёх красках''' — утверждение о том, что всякую расположенную на сфере карту можно раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета. При этом области могут быть как односвязными, так и многосвязными (в них могут присутствовать «дырки»), а под общим участком границы понимается часть линии, то есть стыки нескольких областей в одной точке общей границей для них не считаются. | ||
| + | }} | ||
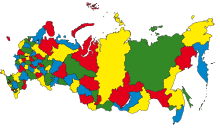
| + | [[Файл:Map of Russia(four colour).png|230px|thumb|right|карта России раскрашенная в <tex>4</tex> цвета]] | ||
| + | Теорема о четырёх красках была доказана в <tex>1976</tex> году Кеннетом Аппелем и Вольфгангом Хакеном из Иллинойского университета. Это была первая крупная математическая теорема, доказанная с помощью компьютера. Первым шагом доказательства была демонстрация того, что существует определенный набор из <tex>1936</tex> карт, ни одна из которых не может содержать карту меньшего размера, которая опровергала бы теорему. Аппель и Хакен использовали специальную компьютерную программу, чтобы доказать это свойство для каждой из <tex>1936</tex> карт. Доказательство этого факта заняло сотни страниц. После этого Аппель и Хакен пришли к выводу, что не существует наименьшего контрпримера к теореме, потому что иначе он должен бы содержать, хотя не содержит, какую-нибудь из этих <tex>1936</tex> карт. Это противоречие говорит о том, что вообще не существует контрпримера. Изначально доказательство не было принято всеми математиками, поскольку его невозможно было проверить вручную. В дальнейшем оно получило более широкое признание, хотя у некоторых долгое время оставались сомнения. | ||
| + | |||
| + | Чтобы развеять оставшиеся сомнения, в <tex>1997</tex> году Робертсон, Сандерс, Сеймур и Томас опубликовали более простое доказательство, использующее аналогичные идеи, но по-прежнему проделанное с помощью компьютера. Кроме того, в <tex>2005</tex> году доказательство было проделано Джорджсом Гонтиром с использованием специализированного программного обеспечения (Coq v7.3.1) | ||
| + | |||
| + | == Эквивалентные формулировки == | ||
| + | В теории графов утверждение теоремы четырёх красок имеет следующие формулировки: | ||
| + | * Хроматическое число планарного графа не превосходит <tex>4</tex>. | ||
| + | * Рёбра произвольной триангуляции сферы можно раскрасить в три краски так, что все стороны каждого треугольника были раскрашены в разные цвета. | ||
| + | |||
| + | == Ложное доказательство == | ||
| + | Ошибочным мнением считается, что решением проблемы четырех красок является - доказательство того, что невозможно начертить карту, на которой было бы всего лишь пять стран и каждая из этих стран примыкала бы к четырем остальным странам. Нетрудно доказать, что такую карту начертить нельзя. Можно предположить, что отсюда автоматически следует решение проблемы четырех красок для всех карт, но такое заключение неверно. | ||
| + | {| cellpadding="0" | ||
| + | | [[Файл:False disproof left.png|230px]] || [[Файл:False disproof right.png|230px]] | ||
| + | |- | ||
| + | |||
| + | |} | ||
| + | Карта(слева) окрашена пятью цветами, и нужно изменить как минимум <tex>4</tex> из <tex>10</tex> регионов, чтобы получить окраску в четыре цвета(справа) | ||
| − | == Источники == | + | == Источники информации == |
| − | + | * [http://matica.org.ua/lektsii-po-diskretnoy-matematike/3-08-6-raskraski-planarnich-grafov matica.org {{---}} Раскраска планарного графа ] | |
| − | + | * [[wikipedia:ru:Проблема четырёх красок | Википедия {{---}} Проблема четырёх красок]] | |
| + | * [[wikipedia:en:Four color theorem | Wikipedia {{---}} Four color theorem]] | ||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Раскраски графов]] | [[Категория: Раскраски графов]] | ||
Текущая версия на 19:42, 4 сентября 2022
Для планарного графа можно дать оценку сверху на хроматическое число.
Содержание
Раскраска в 6 цветов
| Лемма: |
В любом планарном графе существует вершина степени не больше . |
| Доказательство: |
| Предположим это не так. Для любой вершины графа верно . Если сложить это неравенство для всех , получим . Но по следствию из теоремы Эйлера . Пришли к противоречию. |
| Теорема: |
Пусть граф — планарный. Тогда |
| Доказательство: |
|
Докажем по индукции. База индукции Если граф содержит не более вершин, то очевидно, что Индукционный переход Предположим, что для планарного графа с вершинами существует раскраска в цветов. Докажем то же для графа с вершиной. По только что доказанной лемме в найдётся вершина степени не больше . Удалим её; по предположению индукции получившийся граф можно раскрасить в цветов. Вернём удалённую вершину и покрасим её в цвет, не встречающийся среди смежных ей вершин (ведь "занято" максимум цветов). Индукционный переход доказан. |
Раскраска в 5 цветов
| Теорема (Хивуд): |
Пусть граф — планарный. Тогда |
| Доказательство: |
|
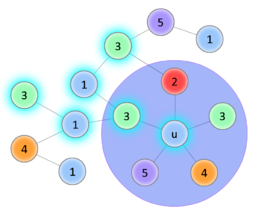
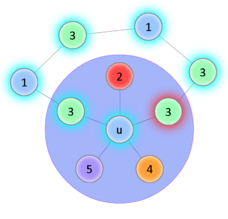
Начало доказательства такое же, как в предыдущей теореме, трудность возникает в индукционном переходе. Покажем что для случая с -ю цветами всё равно можно вернуть удалённую вершину так, чтобы раскраска осталась правильной. Обозначим за — возвращаемую вершину, — вершину, покрашенную в цвет. Если среди вершин, смежных , есть две вершины одного цвета, значит остаётся по меньшей мере один свободный цвет, в который мы и покрасим . Иначе, уложим полученный после удаления граф на плоскость, вернём вершину (пока бесцветную) и пронумеруем цвета в порядке обхода смежных вершин по часовой стрелке. Попробуем покрасить в цвет . Чтобы раскраска осталась правильной, перекрасим смежную ей вершину в цвет . Если среди смежных ей вершин есть вершины , покрасим их в цвет , и так далее. Рассмотрим две необычные ситуации, которые могут наступить во время обхода:
Если этот процесс был успешно завершён, то получили правильную раскраску. Если же в соответствии со вторым вариантом перекраска не удалась, это означает, что в графе есть цикл . Тогда попытаемся таким же образом перекрасить в цвет , а смежную ей в цвет (со последующими перекрасками). Если удастся — раскраска получена. Если нет, то получили ещё один цикл . Но граф планарный, значит два полученных цикла пересекаются помимо вершины по крайней мере ещё в одной, что невозможно, ведь вершины первого цикла и второго — разных цветов. Значит такой случай наступить не мог. |
| Успешное перекрашивание | Цикл 1—3, перекрасить не удаётся | ||||||||||
 |
| ||||||||||
 |
|
Заметим, что не удаётся составить подобное доказательство для раскраски в четыре цвета, поскольку здесь наличие двух вершин одного цвета среди смежных не исключает того, что при их (смежных вершин) раскраске использовались все возможные цвета.
Раскраска в 4 цвета
| Теорема (Проблема четырех красок): |
Теорема о четырёх красках — утверждение о том, что всякую расположенную на сфере карту можно раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета. При этом области могут быть как односвязными, так и многосвязными (в них могут присутствовать «дырки»), а под общим участком границы понимается часть линии, то есть стыки нескольких областей в одной точке общей границей для них не считаются. |
Теорема о четырёх красках была доказана в году Кеннетом Аппелем и Вольфгангом Хакеном из Иллинойского университета. Это была первая крупная математическая теорема, доказанная с помощью компьютера. Первым шагом доказательства была демонстрация того, что существует определенный набор из карт, ни одна из которых не может содержать карту меньшего размера, которая опровергала бы теорему. Аппель и Хакен использовали специальную компьютерную программу, чтобы доказать это свойство для каждой из карт. Доказательство этого факта заняло сотни страниц. После этого Аппель и Хакен пришли к выводу, что не существует наименьшего контрпримера к теореме, потому что иначе он должен бы содержать, хотя не содержит, какую-нибудь из этих карт. Это противоречие говорит о том, что вообще не существует контрпримера. Изначально доказательство не было принято всеми математиками, поскольку его невозможно было проверить вручную. В дальнейшем оно получило более широкое признание, хотя у некоторых долгое время оставались сомнения.
Чтобы развеять оставшиеся сомнения, в году Робертсон, Сандерс, Сеймур и Томас опубликовали более простое доказательство, использующее аналогичные идеи, но по-прежнему проделанное с помощью компьютера. Кроме того, в году доказательство было проделано Джорджсом Гонтиром с использованием специализированного программного обеспечения (Coq v7.3.1)
Эквивалентные формулировки
В теории графов утверждение теоремы четырёх красок имеет следующие формулировки:
- Хроматическое число планарного графа не превосходит .
- Рёбра произвольной триангуляции сферы можно раскрасить в три краски так, что все стороны каждого треугольника были раскрашены в разные цвета.
Ложное доказательство
Ошибочным мнением считается, что решением проблемы четырех красок является - доказательство того, что невозможно начертить карту, на которой было бы всего лишь пять стран и каждая из этих стран примыкала бы к четырем остальным странам. Нетрудно доказать, что такую карту начертить нельзя. Можно предположить, что отсюда автоматически следует решение проблемы четырех красок для всех карт, но такое заключение неверно.
 |

|
Карта(слева) окрашена пятью цветами, и нужно изменить как минимум из регионов, чтобы получить окраску в четыре цвета(справа)