NP-полнота игры Тетрис — различия между версиями
Heatwave (обсуждение | вклад) м (→Формальные правила) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 10 промежуточных версий 4 участников) | |||
| Строка 4: | Строка 4: | ||
: '''Игровое поле''' — расчерченный на клетки прямоугольник размером <tex>m</tex> горизонтальных рядов (строк) на <tex>n</tex> вертикальных (столбцов). Примем следующую индексацию: снизу вверх и слева направо. <math>\langle i, j \rangle</math>-я клетка либо ''свободна'', либо ''занята''. В допустимом состоянии поля ни один горизонтальный ряд не заполнен целиком и нет ни одной полностью пустой строки, которая бы лежала ниже занятой клетки. При оценке допустимости некоторых действий будем считать, что все клетки вне игрового поля всегда заняты и тем самым ограничивают поле. | : '''Игровое поле''' — расчерченный на клетки прямоугольник размером <tex>m</tex> горизонтальных рядов (строк) на <tex>n</tex> вертикальных (столбцов). Примем следующую индексацию: снизу вверх и слева направо. <math>\langle i, j \rangle</math>-я клетка либо ''свободна'', либо ''занята''. В допустимом состоянии поля ни один горизонтальный ряд не заполнен целиком и нет ни одной полностью пустой строки, которая бы лежала ниже занятой клетки. При оценке допустимости некоторых действий будем считать, что все клетки вне игрового поля всегда заняты и тем самым ограничивают поле. | ||
| − | + | {| cellpadding="3" style="margin-left: auto; margin-right: auto;" | |
| + | | [[Файл:SQ.png|50px|thumb|right| SQ]] | ||
| + | | [[Файл:LG.png|50px|thumb|right| LG]] | ||
| + | | [[Файл:RG.png|50px|thumb|right| RG]] | ||
| + | | [[Файл:LS.png|50px|thumb|right| LS]] | ||
| + | | [[Файл:RS.png|50px|thumb|right| RS]] | ||
| + | | [[Файл:I.png|50px|thumb|right| I]] | ||
| + | | [[Файл:T.png|50px|thumb|right| T]] | ||
| + | |} | ||
| + | |||
: '''Игровые фигуры''' — семь различных фигур, получаемых соединением четырех единичных клеток по каким-либо из сторон. Каждая фигура имеет ''центр'' (на илл. 2). ''Состояние фигуры'' <math>P</math> — кортеж из четырех элементов, а именно: | : '''Игровые фигуры''' — семь различных фигур, получаемых соединением четырех единичных клеток по каким-либо из сторон. Каждая фигура имеет ''центр'' (на илл. 2). ''Состояние фигуры'' <math>P</math> — кортеж из четырех элементов, а именно: | ||
| − | # ''тип фигуры'' — SQ, LG, RG, LS, RS, I или T. | + | # ''тип фигуры'' — SQ (''square''), LG (''left gun''), RG (''right gun''), LS (''left snake''), RS (''right snake''), I или T. |
# ''ориентация'' — поворот на 0°, 90°, 180° или 270° по часовой стрелке относительно ''базовой ориентации'' фигуры (на илл. 1). | # ''ориентация'' — поворот на 0°, 90°, 180° или 270° по часовой стрелке относительно ''базовой ориентации'' фигуры (на илл. 1). | ||
# ''позиция'' центра фигуры на поле, выбираемая из <tex>\{1,\dots,m\} \times \{1,\dots,n\}</tex>. Позицией SQ считается местоположение ее левой верхней клетки, так как ее центр лежит на границе четырех клеток, а не внутри одной. | # ''позиция'' центра фигуры на поле, выбираемая из <tex>\{1,\dots,m\} \times \{1,\dots,n\}</tex>. Позицией SQ считается местоположение ее левой верхней клетки, так как ее центр лежит на границе четырех клеток, а не внутри одной. | ||
| − | # значение ''зафиксирована'' или ''не зафиксирована'', определяющее, может ли фигура продолжать двигаться. | + | # значение ''зафиксирована'' (англ. ''fixed'') или ''не зафиксирована'' (англ. ''unfixed''), определяющее, может ли фигура продолжать двигаться. |
В ''исходном'' состоянии фигуры она имеет базовую ориентацию, ее позиция такова, что верхний ряд ее клеток содержится в ряду <math>m</math>, а центр в столбце <math>\lfloor n/2 \rfloor</math>, и она не зафиксирована. | В ''исходном'' состоянии фигуры она имеет базовую ориентацию, ее позиция такова, что верхний ряд ее клеток содержится в ряду <math>m</math>, а центр в столбце <math>\lfloor n/2 \rfloor</math>, и она не зафиксирована. | ||
| Строка 19: | Строка 28: | ||
: '''Игровые действия'''. | : '''Игровые действия'''. | ||
| − | // | + | Для фигуры <math>P=\langle t,o,\langle i,j \rangle , fixed \rangle.</math> допустимых действий нет. Для фигуры <math>P=\langle t,o,\langle i,j \rangle , unfixed \rangle.</math> на данном игровом поле <math>B</math> допустимы следующие действия: |
| + | # ''Поворот по часовой стрелке''. Новым состоянием фигуры будет <math>R(P,90^{\circ},B)</math>. | ||
| + | # ''Поворот против часовой стрелки''. Новым состоянием фигуры будет <math>R(P,-90^{\circ},B)</math>. | ||
| + | # ''Сдвиг влево''. Если клетки слева от фигуры свободны в <math>B</math>, фигура <math>P</math> может быть сдвинута влево на один столбец. Новым состоянием фигуры будет <math>\langle t,o,\langle i,j - 1 \rangle , unfixed \rangle.</math> | ||
| + | # ''Сдвиг вправо''. Аналогично сдвигу влево; новым состоянием будет <math>\langle t,o,\langle i,j + 1 \rangle , unfixed \rangle.</math> | ||
| + | # ''Снижение'' на один ряд, если все клетки под фигурой свободны в <math>B</math>. Новое состояние — <math>\langle t,o,\langle i - 1,j \rangle , unfixed \rangle.</math> | ||
| + | # ''Фиксация'', если хотя бы одна клетка под фигурой занята в <math>B</math>. Новое состояние — <math>\langle t,o,\langle i,j \rangle , fixed \rangle.</math> | ||
| + | |||
| + | ''Траекторией'' <math>\sigma</math> фигуры <math>P</math> называется последовательность допустимых действий, начинающихся в исходном состоянии и заканчивающихся действием-фиксацией. Результатом траектории фигуры <math>P</math> на игровом поле <math>B</math> является новое поле <math>B'</math>, определяемое следующим образом: | ||
| + | # Новое поле <math>B'</math> — это поле <math>B</math> с заполненными клетками фигуры <math>P</math>. | ||
| + | # Если фигура зафиксирована таким образом, что для некоторого горизонтального ряда <math>r</math> каждая клетка <math>r</math> в поле <math>B'</math> заполнена, то ряд <math>r</math> ''освобождается''. Для всех <math>r' \geqslant r</math> следует заменить ряд <math>r'</math> в <math>B'</math> рядом <math>r'+1</math> в <math>B'</math>. Ряд <math>m</math> в <math>B'</math> становится пустым. Фиксация одной фигуры может привести к освобождению более чем одного ряда. | ||
| + | # Если исходное состояние следующей фигуры в <math>B'</math> заблокировано, игра заканчивается (игрок ''проигрывает''). | ||
| + | |||
| + | Для ''игры'' <math>\langle B_0,P_1,\dots,P_p \rangle</math>, ''последовательностью траекторий'' <math>\Sigma</math> является такая последовательность <math> B_0,\sigma_1,B_1,\dots,\sigma_p,B_p</math>, что для любого <math>i</math> траектория фигуры <math>P_i</math> на поле <math>B_{i-1}</math> приводит к полю <math>B_i</math>. Однако, если существует действие <math>\sigma_q</math> при некотором <math>q \leqslant p</math>, приводящее к проигрышу, то последовательность <math>\Sigma</math> завершается на <math>B_q</math>, а не на <math>B_p</math>. | ||
| + | |||
| + | ==NP-полнота игры== | ||
| + | |||
| + | Рассмотрим следующую проблему, называемую '''k-cleared rows''' (<math>G,\Sigma</math>): в игре <math>G</math>, приводит ли <math>\Sigma</math> к освобождению хотя бы <math>k</math> рядов до проигрыша? Вспомним проблему 3-Partition, которая является NP-полной. Формальное ее условие таково: ввод — последовательность целых чисел <math>a_1,a_2,\dots,a_{3s}</math> и неотрицательное число <math>T</math> такое, что <math>T/4 < a_i < T/2</math> для всех <math>1\leqslant i \leqslant 3s</math>, <tex>\sum_{i=1}^{3s} a_i = sT</tex>; вывод — можно ли <math>\{a_1,\dots,a_{3s}\}</math> разбить на <math>s</math> непересекающихся подмножеств <math>A_1,\dots,A_s</math> так, что для всех <math>1\leqslant j \leqslant s</math> выполняется <tex>\sum_{a_i \in A_j} a_i = T</tex>. | ||
| + | |||
| + | {{Теорема | ||
| + | |statement= | ||
| + | 3-Partition сводится к k-cleared rows. | ||
| + | |proof= | ||
| + | |||
| + | Опишем отображение из 3-Partition в k-cleared-rows. Для заданного ввода 3-Partition <math>P = \langle a_1,\dots,a_{3s},T \rangle</math>, составим игру <math>G(P)</math>, поле которой может быть полностью очищено, только если для <math>P</math> в задаче 3-Partition ответ положительный. | ||
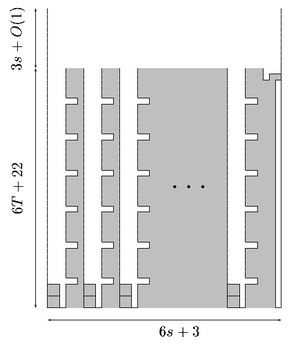
| + | [[Файл:board_partition.png|300px|thumb|right| Начальное игровое поле]] | ||
| + | Начальное игровое поле содержит <math>s</math> ''контейнеров'', соответствующих множествам <math>A_1,\dots,A_s</math> в задаче 3-Partition. Последовательность фигур состоит из некоторого числа фигур, соответствующих каждому из <math>a_i</math> и подобранных так, что все фигуры для <math>a_i</math> должны быть помещены в один и тот же контейнер. Существует подходящее решение задачи 3-Partition для <math>\{a_1,\dots,a_{3s}\}</math> в том и только том случае, когда наборы фигур во всех контейнерах имеют одинаковую высоту. Последние три столбца в игровом поле представляют собой ''стопор'', который не дает очистить ряды, пока не подойдет к концу последовательность фигур; если все контейнеры заполнены на одинаковую высоту, то все поле может быть очищено с помощью последней (завершающей) части последовательности. | ||
| + | Игра <math>G</math> состоит из следующих компонент: | ||
| + | |||
| + | : '''Начальное игровое поле.''' Поле имеет <math>6T + 22 + (3s + O(1))</math> строк и <math>6s + 3</math> столбцов. Каждое <math>a_i</math> будет представлено <math>a_i + 1</math> блоками размером <math>6 \times 6 </math>; так как сумма элементов <math>A_j = \{a_i,a_j,a_k\}</math> равна <math>T</math>, получаем <math>6(T+3)=6T+18</math>. В дополнение к этим <math>6T+18</math> рядам, внизу находятся четыре ряда, обеспечивающие корректное положение блокам. | ||
| + | Верхние <math>3s+O(1)</math> рядов (<math>O(1)</math> — это размер окрестности в модели вращения) изначально пусты и представляют собой промежуточную зону, где фигуру можно вращать и двигать, прежде чем она попадет в нижние <math>6T+22</math> рядов. Остальная часть поля может быть логически разделена на <math>s+1</math> части, где первые <math>s</math> частей имеют шесть клеток в ширину, а последняя — три клетки в ширину. Первые <math>s</math> частей — это контейнеры, имеющие следующий вид: | ||
| + | # В первом и втором столбцах пусты все клетки, кроме нижних четырех. | ||
| + | # Третий столбец не имеет занятых клеток. | ||
| + | # В четвертом и пятом столбцах пусты только клетки в тех строках, чей номер по модулю 6 равен 5. | ||
| + | # Шестой столбец не имеет пустых клеток. | ||
| + | |||
| + | Последняя логическая часть — стопор шириной в три клетки: | ||
| + | # В первом столбце заполнены все клетки, кроме двух верхних. | ||
| + | # Во втором столбце заполнены все клетки, кроме верхней. | ||
| + | # В третьей колонке пусты все клетки, кроме второй сверху. | ||
| + | |||
| + | : '''Фигуры.''' Последовательностью фигур для всей игры будет конкатенация последовательностей для каждого <math>a_i</math> и завершающей последовательности. Для каждого числа <math>a_1,\dots,a_{3s}</math> имеем следующие части: | ||
| + | # ''Инициатор'' — последовательность <math>\langle I,LG,SQ \rangle</math>. | ||
| + | # ''Наполнитель'' — последовательность <math>\langle LG,LS,LG,LG,SQ \rangle</math>, повторенная <math>a_i</math> раз. | ||
| + | # ''Завершитель''— последовательность <math>\langle SQ,SQ \rangle</math>. | ||
| + | Вышеописанные части подаются для <math>a_1,a_2,\dots</math> последовательно. После частей, соответствующих <math>a_{3s}</math>, идет завершающая последовательность: | ||
| + | # <math>s</math> фигур <math>I</math> подряд. | ||
| + | # одна фигура <math>RG</math>. | ||
| + | # <math>3T/2 + 5</math> фигур <math>I</math> подряд. | ||
| + | |||
| + | //продолжение | ||
| + | }} | ||
| + | |||
| + | == Источники информации == | ||
| + | * [http://arxiv.org/abs/cs/0210020 «Tetris is Hard, Even to Approximate» by Erik D. Demaine, Susan Hohenberger, David Liben-Nowell] | ||
| + | |||
| + | [[Категория:NP]] | ||
Текущая версия на 19:42, 4 сентября 2022
Тетрис — популярная игра, созданная в середине 1980-х математиком Алексеем Пажитновым.
Формальные правила
- Игровое поле — расчерченный на клетки прямоугольник размером горизонтальных рядов (строк) на вертикальных (столбцов). Примем следующую индексацию: снизу вверх и слева направо. -я клетка либо свободна, либо занята. В допустимом состоянии поля ни один горизонтальный ряд не заполнен целиком и нет ни одной полностью пустой строки, которая бы лежала ниже занятой клетки. При оценке допустимости некоторых действий будем считать, что все клетки вне игрового поля всегда заняты и тем самым ограничивают поле.
- Игровые фигуры — семь различных фигур, получаемых соединением четырех единичных клеток по каким-либо из сторон. Каждая фигура имеет центр (на илл. 2). Состояние фигуры — кортеж из четырех элементов, а именно:
- тип фигуры — SQ (square), LG (left gun), RG (right gun), LS (left snake), RS (right snake), I или T.
- ориентация — поворот на 0°, 90°, 180° или 270° по часовой стрелке относительно базовой ориентации фигуры (на илл. 1).
- позиция центра фигуры на поле, выбираемая из . Позицией SQ считается местоположение ее левой верхней клетки, так как ее центр лежит на границе четырех клеток, а не внутри одной.
- значение зафиксирована (англ. fixed) или не зафиксирована (англ. unfixed), определяющее, может ли фигура продолжать двигаться.
В исходном состоянии фигуры она имеет базовую ориентацию, ее позиция такова, что верхний ряд ее клеток содержится в ряду , а центр в столбце , и она не зафиксирована.
- Поворот фигуры. Модель поворота — функция , где и — состояния фигуры, — угол поворота, а — игровое поле. На налагаются следующие условия:
- Если и поворот допустим, то для некоторых и . Если поворот недопустим, то .
- При определении допустимости поворота, рассматривает окрестность констатного размера у фигуры — то есть, только клетки на заданном расстоянии от позиции влияют на , а положение фигуры на игровом поле значения не имеет.
- Если все клетки в окрестности свободны, то поворот допустим.
- Если поворот допустим, то не занимает ни одной клетки, уже занятой в .
- Игровые действия.
Для фигуры допустимых действий нет. Для фигуры на данном игровом поле допустимы следующие действия:
- Поворот по часовой стрелке. Новым состоянием фигуры будет .
- Поворот против часовой стрелки. Новым состоянием фигуры будет .
- Сдвиг влево. Если клетки слева от фигуры свободны в , фигура может быть сдвинута влево на один столбец. Новым состоянием фигуры будет
- Сдвиг вправо. Аналогично сдвигу влево; новым состоянием будет
- Снижение на один ряд, если все клетки под фигурой свободны в . Новое состояние —
- Фиксация, если хотя бы одна клетка под фигурой занята в . Новое состояние —
Траекторией фигуры называется последовательность допустимых действий, начинающихся в исходном состоянии и заканчивающихся действием-фиксацией. Результатом траектории фигуры на игровом поле является новое поле , определяемое следующим образом:
- Новое поле — это поле с заполненными клетками фигуры .
- Если фигура зафиксирована таким образом, что для некоторого горизонтального ряда каждая клетка в поле заполнена, то ряд освобождается. Для всех следует заменить ряд в рядом в . Ряд в становится пустым. Фиксация одной фигуры может привести к освобождению более чем одного ряда.
- Если исходное состояние следующей фигуры в заблокировано, игра заканчивается (игрок проигрывает).
Для игры , последовательностью траекторий является такая последовательность , что для любого траектория фигуры на поле приводит к полю . Однако, если существует действие при некотором , приводящее к проигрышу, то последовательность завершается на , а не на .
NP-полнота игры
Рассмотрим следующую проблему, называемую k-cleared rows (): в игре , приводит ли к освобождению хотя бы рядов до проигрыша? Вспомним проблему 3-Partition, которая является NP-полной. Формальное ее условие таково: ввод — последовательность целых чисел и неотрицательное число такое, что для всех , ; вывод — можно ли разбить на непересекающихся подмножеств так, что для всех выполняется .
| Теорема: |
3-Partition сводится к k-cleared rows. |
| Доказательство: |
|
Опишем отображение из 3-Partition в k-cleared-rows. Для заданного ввода 3-Partition , составим игру , поле которой может быть полностью очищено, только если для в задаче 3-Partition ответ положительный. Начальное игровое поле содержит контейнеров, соответствующих множествам в задаче 3-Partition. Последовательность фигур состоит из некоторого числа фигур, соответствующих каждому из и подобранных так, что все фигуры для должны быть помещены в один и тот же контейнер. Существует подходящее решение задачи 3-Partition для в том и только том случае, когда наборы фигур во всех контейнерах имеют одинаковую высоту. Последние три столбца в игровом поле представляют собой стопор, который не дает очистить ряды, пока не подойдет к концу последовательность фигур; если все контейнеры заполнены на одинаковую высоту, то все поле может быть очищено с помощью последней (завершающей) части последовательности. Игра состоит из следующих компонент:
Верхние рядов ( — это размер окрестности в модели вращения) изначально пусты и представляют собой промежуточную зону, где фигуру можно вращать и двигать, прежде чем она попадет в нижние рядов. Остальная часть поля может быть логически разделена на части, где первые частей имеют шесть клеток в ширину, а последняя — три клетки в ширину. Первые частей — это контейнеры, имеющие следующий вид:
Последняя логическая часть — стопор шириной в три клетки:
Вышеописанные части подаются для последовательно. После частей, соответствующих , идет завершающая последовательность:
|