Тьюринг-полнота — различия между версиями
Romanosov (обсуждение | вклад) м (→Источники информации) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 38 промежуточных версий 9 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | ==Введение== | |
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | Вычислительное устройство является '''Тьюринг-эквивалентным''', если оно может эмулировать машину Тьюринга. | + | Вычислительное устройство является '''Тьюринг-эквивалентным''' (англ. ''Turing-equivalent''), если оно может эмулировать [[Машина Тьюринга|машину Тьюринга]]. |
}} | }} | ||
| + | {{Определение | ||
| + | |definition = | ||
| + | Задача называется '''Тьюринг-полной''' (англ. ''Turing-complete''), если её можно решить, используя только машину Тьюринга или любую систему, являющуюся Тьюринг-эквивалентной. | ||
| + | }} | ||
| + | |||
Зачастую Тьюринг-эквивалентные языки программирования называют Тьюринг-полными. | Зачастую Тьюринг-эквивалентные языки программирования называют Тьюринг-полными. | ||
В теории вычислимости ''исполнитель'' (множество вычисляющих элементов) называется '''Тьюринг-полным''', если на нём можно реализовать любую вычислимую функцию. Другими словами, для каждой вычислимой функции существует вычисляющий её элемент (например, машина Тьюринга) или программа для исполнителя, а все функции, вычисляемые множеством вычислителей, являются вычислимыми функциями (возможно, при некотором кодировании входных и выходных данных). | В теории вычислимости ''исполнитель'' (множество вычисляющих элементов) называется '''Тьюринг-полным''', если на нём можно реализовать любую вычислимую функцию. Другими словами, для каждой вычислимой функции существует вычисляющий её элемент (например, машина Тьюринга) или программа для исполнителя, а все функции, вычисляемые множеством вычислителей, являются вычислимыми функциями (возможно, при некотором кодировании входных и выходных данных). | ||
| − | Любой полный по Тьюрингу язык достаточно | + | Любой полный по Тьюрингу язык достаточно универсален, чтобы иметь возможность имитировать любой другой язык (хотя и с потенциальным замедлением в работе). Такие языки эквивалентны в рамках вычислений, которые могут произвести. Полные по Тьюрингу языки настолько распространены, что их можно обнаружить даже в примитивных на первый взгляд системах, например, [[Линейный клеточный автомат, эквивалентность МТ | клеточных автоматах]] или мозаичных системах. |
| − | |||
| − | |||
| + | На практике полнота по Тьюрингу похожа на идеализацию. Компьютеры имеют ограниченное количество памяти, а неограниченная по времени их работа может быть прервана физическим воздействием (выключение, поломка), что как бы ограничивает число задач, которые они могут решить. На самом деле, физические ограничения в контексте Тьюринг-полноты не берутся во внимание: Тьюринг-полный исполнитель не должен быть ограничен по времени и памяти лишь самим исполнителем. | ||
==Критерии Тьюринг-полноты== | ==Критерии Тьюринг-полноты== | ||
| − | Если на языке программирования можно реализовать машину Тьюринга, то такой язык Тьюринг-полон, и наоборот. Возможность реализации машины Тьюринга на конкретном языке программирования можно грубо описать как перечень требований, которым этот язык должен для этого удовлетворять: | + | Если на языке программирования можно реализовать машину Тьюринга, то такой язык Тьюринг-полон, и наоборот. Возможность реализации машины Тьюринга на конкретном языке программирования можно ''грубо'' описать как перечень требований, которым этот язык должен для этого удовлетворять: |
| − | * Конечность (нет бесконечных символьных множеств и пр.) | + | * Конечность (нет бесконечных символьных множеств и пр.). |
| − | * Фиксированное описание | + | * Фиксированное описание (формальность<ref>[https://ru.wikipedia.org/wiki/%D0%A4%D0%BE%D1%80%D0%BC%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D1%8F%D0%B7%D1%8B%D0%BA Википедия — Формальный язык]</ref>). |
| − | * Всегда достаточный объём доступной памяти — в идеале здесь имеется в виду | + | * Всегда достаточный объём доступной памяти — в идеале здесь имеется в виду неограниченная память, однако физические рамки не позволяют сделать память ЭВМ бесконечной, поэтому она просто должна быть ''"always big enough"''. |
| − | * Неограниченность времени выполнения | + | * Неограниченность времени выполнения — любая программа в должна иметь возможность работать до тех пор, пока не завершится. |
| − | * Возможность функциональной композиции (вызов одной функции из другой, рекурсия) | + | * Возможность функциональной композиции (вызов одной функции из другой, рекурсия). |
| − | * | + | * Наличие циклов <tex>{\bf while}</tex> с прерыванием или эквивалентных им конструкций. |
| − | * Возможность останавливать выполнение (halt) или каким-то образом подавать сигнал о результатах выполнения | + | * Возможность останавливать выполнение (''halt'') или каким-то образом подавать сигнал о результатах выполнения. |
| − | * Представление множества натуральных чисел, понятие | + | * Представление множества натуральных чисел, понятие нуля и следующего числа. Возможны другие подобные системы. |
| − | * Поддержка входных и выходных данных (I/O), причём без ограничений в объёме. | + | * Поддержка входных и выходных данных (I/O), причём без формальных ограничений в объёме. Очевидно, что если любая программа, написанная на каком-то языке программирования, принимает на вход не более фиксированного n бит данных и возвращает не более n бит, этот язык не может быть Тьюринг-полным. |
==Тьюринг-полнота и неполнота некоторых языков программирования== | ==Тьюринг-полнота и неполнота некоторых языков программирования== | ||
| − | Доказать Тьюринг-полноту языка программирования можно, предложив способ реализации машины Тьюринга на этом языке. Кроме того, можно предложить интерпретатор | + | Доказать Тьюринг-полноту языка программирования можно, предложив способ реализации машины Тьюринга на этом языке. Кроме того, можно предложить на нём интерпретатор Тьюринг-полного языка. |
===Assembly language=== | ===Assembly language=== | ||
| − | Язык Ассемблера | + | Язык Ассемблера достаточно примитивен относительно языков программирования высокого уровня: он рассчитан на архитектуру с конечной памятью и работает с конечным набором регистров. Однако, не был бы он полным по Тьюрингу, не были бы Тьюринг-полны и любые высокоуровневые языки программирования. |
Всё необходимое для машины Тьюринга на asm можно сделать примерно так: | Всё необходимое для машины Тьюринга на asm можно сделать примерно так: | ||
| − | ADDS r0, r0, #1 ; сдвиг ленты вправо | + | ADDS r0, r0, #1 <font color=green>; сдвиг ленты вправо</font> |
| − | ADDS r0, r0, #-1 ; сдвиг ленты влево | + | ADDS r0, r0, #-1 <font color=green>; сдвиг ленты влево</font> |
| − | ADDS [r0], [r0], #1 ; инкремент значения, на которое "указывает" головка ленты | + | ADDS [r0], [r0], #1 <font color=green>; инкремент значения, на которое "указывает" головка ленты</font> |
| − | ADDS [r0], [r0], #-1 ; декремент значения, на которое "указывает" головка ленты | + | ADDS [r0], [r0], #-1 <font color=green>; декремент значения, на которое "указывает" головка ленты</font> |
| − | И далее использовать инструкцию | + | И далее использовать инструкцию <tex>\mathrm{BEQ}</tex> или ей подобную, чтобы выполнять определённую последовательность команд при определённом текущем значении, таким образом обеспечив ветвление. |
===Pascal=== | ===Pascal=== | ||
| − | Язык Pascal позволяет смоделировать ленту машины Тьюринга с помощью двунаправленного списка из переменных, создаваемых оператором | + | Язык Pascal позволяет смоделировать ленту машины Тьюринга с помощью двунаправленного списка из переменных, создаваемых оператором <tex>\mathrm{new}</tex>, семантика которого не предполагает отказа в создании переменной. Также с помощью списков |
можно смоделировать сколь угодно большие числа. Стандарт не накладывает никаких ограничений: указательный тип абстрактен, множество значений указательного типа языком не ограничено. | можно смоделировать сколь угодно большие числа. Стандарт не накладывает никаких ограничений: указательный тип абстрактен, множество значений указательного типа языком не ограничено. | ||
В Паскале есть еще один тип данных с неограниченным множеством значений, файловый, также пригодный для моделирования ленты машины Тьюринга и представления больших чисел. Достаточно утверждений для очевидности Тьюринг-полноты языка Pascal. | В Паскале есть еще один тип данных с неограниченным множеством значений, файловый, также пригодный для моделирования ленты машины Тьюринга и представления больших чисел. Достаточно утверждений для очевидности Тьюринг-полноты языка Pascal. | ||
| Строка 64: | Строка 68: | ||
===SQL=== | ===SQL=== | ||
| − | Сам по себе SQL не | + | Сам по себе SQL никогда не считался полным по Тьюрингу языком. Однако, у него существует множество расширений, позволяющих делать рекурсивные запросы, циклы, списки, деревья и пр., например, с помощью PostgreSQL<ref>[http://assets.en.oreilly.com/1/event/27/High%20Performance%20SQL%20with%20PostgreSQL%20Presentation.pdf High Performance with PostgreSQL 8.4]</ref>. Более того, на в 2011 г. Habrahabr появилась статья, где показана машина Тьюринга на SQL<ref>[https://habrahabr.ru/post/113165/|Машина Тьюринга на чистом SQL]</ref> (в реализации Firebird 2.1, который ограничивает вложенность рекурсивных запросов до 2014 уровней). Тем не менее, всё ещё остаётся ограниченное query execution time. |
===HTML=== | ===HTML=== | ||
| Строка 77: | Строка 81: | ||
!style="background-color:#EEE;padding:2px 8px"| '''Парадигма''' | !style="background-color:#EEE;padding:2px 8px"| '''Парадигма''' | ||
!style="background-color:#EEE;padding:2px 8px"| '''Уровень''' | !style="background-color:#EEE;padding:2px 8px"| '''Уровень''' | ||
| − | !style="background-color:#EEE;padding:2px 8px"| ''' | + | !style="background-color:#EEE;padding:2px 8px"| '''Зависимость от архитектуры процессора''' |
!style="background-color:#EEE;padding:2px 8px"| '''Полнота по Тьюрингу''' | !style="background-color:#EEE;padding:2px 8px"| '''Полнота по Тьюрингу''' | ||
|- | |- | ||
| Строка 137: | Строка 141: | ||
|- | |- | ||
|style="background-color:#FFF;padding:2px 8px"| JavaScript | |style="background-color:#FFF;padding:2px 8px"| JavaScript | ||
| − | |style="background-color:#FFF;padding:2px 8px"| | + | |style="background-color:#FFF;padding:2px 8px"| 1995 |
|style="background-color:#FFF;padding:2px 8px"| Объектно-ориентированный | |style="background-color:#FFF;padding:2px 8px"| Объектно-ориентированный | ||
|style="background-color:#FFF;padding:2px 8px"| Высокий | |style="background-color:#FFF;padding:2px 8px"| Высокий | ||
| Строка 191: | Строка 195: | ||
===mov=== | ===mov=== | ||
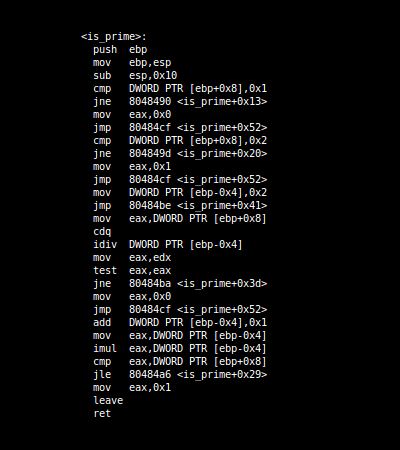
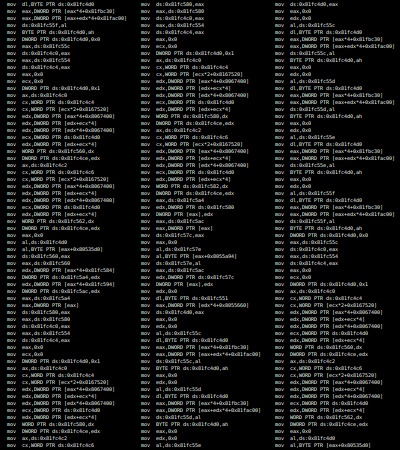
| − | Утилита M/o/Vfuscator превращает любую программу на языке C в огромную последовательность из инструкций mov<ref>[https://github.com/xoreaxeaxeax/movfuscator M/o/Vfuscator]</ref>. | + | Утилита M/o/Vfuscator превращает любую программу на языке C в огромную последовательность из инструкций <tex>\mathrm {mov}</tex><ref>[https://github.com/xoreaxeaxeax/movfuscator M/o/Vfuscator]</ref>. |
| + | |||
| + | {| cellpadding="0" style= align="left"; | ||
| + | |[[Файл:gcc_asm.png|400px|thumb|left|Результат работы GCC]] | ||
| + | |[[Файл:mov_asm.png|400px|thumb|left|Результат работы M/o/Vfuscator]] | ||
| + | |} | ||
| − | {| cellpadding=" | + | {| cellpadding="0" style= align="left"; |
| − | + | |[[Файл:Demo_mov.gif|thumb|500px|left|Простые числа с использованием одной инструкции]] | |
| − | |||
| − | |[[Файл:Demo_mov.gif| | ||
|} | |} | ||
| Строка 203: | Строка 210: | ||
Нововведения новых версий HTML/CSS позволяют построить<ref>[http://eli.fox-epste.in/rule110-full.html Rule 110]</ref> [https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D0%BE_110 правило 110], которое является Тьюринг-полным. | Нововведения новых версий HTML/CSS позволяют построить<ref>[http://eli.fox-epste.in/rule110-full.html Rule 110]</ref> [https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D0%BE_110 правило 110], которое является Тьюринг-полным. | ||
| − | === | + | ===Excel=== |
| + | |||
| + | Excel имеет свой скриптовый язык. Однако, для кодирования Машины Тьюринга в таблице Excel достаточно использование только формул<ref>[http://www.felienne.com/archives/2974 Excel Turing Machine]</ref>. | ||
| − | === | + | ===Тьюринг-полнота в играх=== |
| − | + | * Minecraft<ref>[https://www.youtube.com/watch?v=7sNge0Ywz-M|Demonstrating the CPU. Then coughing a lot. Sorry about that. I may be dying.]</ref>. Возможно, достижение Тьюринг-полноты в игре-песочнице с возможностью создания логических элементов было неизбежным, но сложность компьютеров, собираемых из блоков в данной игре, достойна внимания. | |
| − | = | + | * Little Big Planet<ref>[https://www.youtube.com/watch?v=13GOFa1C4e4| LittleBigLife — The Game of Life in LittleBigPlanet]</ref>. Некоторые элементы игры представляют из себя ничто иное, как небольшие клеточные автоматы, которые можно запрограммировать. |
| − | = | + | * Super Mario World<ref>[https://www.youtube.com/watch?v=hB6eY73sLV0 SNES Code Injection -- Flappy Bird in SMW]</ref>. Умелое обращение с багами игры позволяет сделать в ней буквально всё, что позволяет 2d-пространство Nintendo. |
| + | |||
| + | * [[Неразрешимость игры Braid|Braid]]. | ||
==Тьюринговская трясина== | ==Тьюринговская трясина== | ||
| Строка 217: | Строка 228: | ||
'''Тьюринговская трясина''' — жаргонное общее название для языков программирования, которые ''Тьюринг-полны'', но обладают крайне примитивными синтаксисом и семантикой. Они неудобны для практического программирования (из-за трудности написания программ и низкой производительности), зато хорошо подходят для некоторых других задач (доказательство невычислимости некоторых функций, иллюстрация базовых принципов программирования и т. д.). Поэтому они интересны для информатики. | '''Тьюринговская трясина''' — жаргонное общее название для языков программирования, которые ''Тьюринг-полны'', но обладают крайне примитивными синтаксисом и семантикой. Они неудобны для практического программирования (из-за трудности написания программ и низкой производительности), зато хорошо подходят для некоторых других задач (доказательство невычислимости некоторых функций, иллюстрация базовых принципов программирования и т. д.). Поэтому они интересны для информатики. | ||
| − | Первыми представителями | + | Первыми представителями «трясины» были ''лямбда-исчисление'', ''комбинаторная логика'' и сама машина Тьюринга. |
Многие эзотерические языки программирования также являются «трясинами Тьюринга» (напр. Brainfuck, Spoon, Malbolge, Whitespace). | Многие эзотерические языки программирования также являются «трясинами Тьюринга» (напр. Brainfuck, Spoon, Malbolge, Whitespace). | ||
| + | |||
| + | ==Проблема остановки== | ||
| + | {{Определение | ||
| + | |definition= Проблема остановки {{---}} проблема определения факта остановки данной машины Тьюринга на данных входных данных (закончит выполнение или нет). | ||
| + | }} | ||
| + | {{Теорема | ||
| + | |statement= Проблема остановки неразрешима | ||
| + | |proof= Докажем от противного. Предположим существует такая полностью вычислимая функция <tex>halts(f)</tex>, которая возвращает <tex>true</tex>, если функция <tex>f</tex> остановится когда-либо, и <tex>false</tex>, если функция <tex>f</tex> никогда не остановится. | ||
| + | |||
| + | Рассмотрим следующую функцию <tex>g</tex> | ||
| + | |||
| + | '''void''' g(): | ||
| + | '''if''' halts(g): | ||
| + | '''for'''(;;) | ||
| + | <tex>halts(g)</tex> должна возвращать либо <tex>true</tex>, либо <tex>false</tex>. | ||
| + | * Если <tex>halts(g)</tex> вернула <tex>true</tex>, то <tex>g</tex> никогда не остановится, получили противоречие | ||
| + | * Если <tex>halts(g)</tex> вернула <tex>false</tex>, то <tex>g</tex> остановится, получили противоречие | ||
| + | }} | ||
| + | |||
| + | ==Теорема Геделя о неполноте== | ||
| + | Чтобы доказать теорему, можно воспользоваться проблемой остановки машины Тьюринга. | ||
| + | {{Теорема | ||
| + | |statement= Любая непротиворечивая формальная система аксиом <tex>T</tex>, способная выражать утверждения о натуральных числах и доказывать простые арифметические факты, неполна {{---}} существуют утверждения о натуральных числах, которые она не может ни доказать, ни опровергнуть. | ||
| + | |proof= | ||
| + | # Предположим, что система <tex>T</tex> полна, т.е. доказывает или опровергает любое утверждение. | ||
| + | # Сформулируем и запишем на языке арифметики утверждение <tex>O</tex> = "машина Тьюринга <tex>M</tex> точно остановится, если запустить ее с данными <tex>D</tex>". | ||
| + | # Переберем все доказательства (<tex>P</tex> {{---}} истинно) и опровержения (<tex>\neg P</tex> {{---}} истинно) в системе <tex>T</tex>, чья длина совпадает с длиной <tex>O</tex>. | ||
| + | # Так как система <tex>T</tex> полна, рано или поздно мы найдем опровержение или доказательство утверждения <tex>O</tex> | ||
| + | # Система <tex>T</tex> доказывает не только истинные факты (так как она только непротиворечива), т.е. доказываемое утверждение может быть ложным. | ||
| + | # Тем не менее, мы фактически решили проблему остановки. | ||
| + | }} | ||
==См. также== | ==См. также== | ||
| − | [[Машина Тьюринга]] | + | * [[Машина Тьюринга]] |
| + | |||
| + | * [[Лямбда-исчисление]] | ||
| + | |||
| + | * [[Игра «Жизнь»]] | ||
| + | |||
| + | * [[Busy beaver]] | ||
==Примечания== | ==Примечания== | ||
| Строка 251: | Строка 299: | ||
[[Категория: Теория формальных языков]] | [[Категория: Теория формальных языков]] | ||
[[Категория: Теория вычислимости]] | [[Категория: Теория вычислимости]] | ||
| + | [[Категория: Вычислительные формализмы]] | ||
| + | [[Категория: Машина Тьюринга]] | ||
Текущая версия на 19:42, 4 сентября 2022
Содержание
Введение
| Определение: |
| Вычислительное устройство является Тьюринг-эквивалентным (англ. Turing-equivalent), если оно может эмулировать машину Тьюринга. |
| Определение: |
| Задача называется Тьюринг-полной (англ. Turing-complete), если её можно решить, используя только машину Тьюринга или любую систему, являющуюся Тьюринг-эквивалентной. |
Зачастую Тьюринг-эквивалентные языки программирования называют Тьюринг-полными.
В теории вычислимости исполнитель (множество вычисляющих элементов) называется Тьюринг-полным, если на нём можно реализовать любую вычислимую функцию. Другими словами, для каждой вычислимой функции существует вычисляющий её элемент (например, машина Тьюринга) или программа для исполнителя, а все функции, вычисляемые множеством вычислителей, являются вычислимыми функциями (возможно, при некотором кодировании входных и выходных данных).
Любой полный по Тьюрингу язык достаточно универсален, чтобы иметь возможность имитировать любой другой язык (хотя и с потенциальным замедлением в работе). Такие языки эквивалентны в рамках вычислений, которые могут произвести. Полные по Тьюрингу языки настолько распространены, что их можно обнаружить даже в примитивных на первый взгляд системах, например, клеточных автоматах или мозаичных системах.
На практике полнота по Тьюрингу похожа на идеализацию. Компьютеры имеют ограниченное количество памяти, а неограниченная по времени их работа может быть прервана физическим воздействием (выключение, поломка), что как бы ограничивает число задач, которые они могут решить. На самом деле, физические ограничения в контексте Тьюринг-полноты не берутся во внимание: Тьюринг-полный исполнитель не должен быть ограничен по времени и памяти лишь самим исполнителем.
Критерии Тьюринг-полноты
Если на языке программирования можно реализовать машину Тьюринга, то такой язык Тьюринг-полон, и наоборот. Возможность реализации машины Тьюринга на конкретном языке программирования можно грубо описать как перечень требований, которым этот язык должен для этого удовлетворять:
- Конечность (нет бесконечных символьных множеств и пр.).
- Фиксированное описание (формальность[1]).
- Всегда достаточный объём доступной памяти — в идеале здесь имеется в виду неограниченная память, однако физические рамки не позволяют сделать память ЭВМ бесконечной, поэтому она просто должна быть "always big enough".
- Неограниченность времени выполнения — любая программа в должна иметь возможность работать до тех пор, пока не завершится.
- Возможность функциональной композиции (вызов одной функции из другой, рекурсия).
- Наличие циклов с прерыванием или эквивалентных им конструкций.
- Возможность останавливать выполнение (halt) или каким-то образом подавать сигнал о результатах выполнения.
- Представление множества натуральных чисел, понятие нуля и следующего числа. Возможны другие подобные системы.
- Поддержка входных и выходных данных (I/O), причём без формальных ограничений в объёме. Очевидно, что если любая программа, написанная на каком-то языке программирования, принимает на вход не более фиксированного n бит данных и возвращает не более n бит, этот язык не может быть Тьюринг-полным.
Тьюринг-полнота и неполнота некоторых языков программирования
Доказать Тьюринг-полноту языка программирования можно, предложив способ реализации машины Тьюринга на этом языке. Кроме того, можно предложить на нём интерпретатор Тьюринг-полного языка.
Assembly language
Язык Ассемблера достаточно примитивен относительно языков программирования высокого уровня: он рассчитан на архитектуру с конечной памятью и работает с конечным набором регистров. Однако, не был бы он полным по Тьюрингу, не были бы Тьюринг-полны и любые высокоуровневые языки программирования.
Всё необходимое для машины Тьюринга на asm можно сделать примерно так:
ADDS r0, r0, #1 ; сдвиг ленты вправо ADDS r0, r0, #-1 ; сдвиг ленты влево ADDS [r0], [r0], #1 ; инкремент значения, на которое "указывает" головка ленты ADDS [r0], [r0], #-1 ; декремент значения, на которое "указывает" головка ленты
И далее использовать инструкцию или ей подобную, чтобы выполнять определённую последовательность команд при определённом текущем значении, таким образом обеспечив ветвление.
Pascal
Язык Pascal позволяет смоделировать ленту машины Тьюринга с помощью двунаправленного списка из переменных, создаваемых оператором , семантика которого не предполагает отказа в создании переменной. Также с помощью списков можно смоделировать сколь угодно большие числа. Стандарт не накладывает никаких ограничений: указательный тип абстрактен, множество значений указательного типа языком не ограничено. В Паскале есть еще один тип данных с неограниченным множеством значений, файловый, также пригодный для моделирования ленты машины Тьюринга и представления больших чисел. Достаточно утверждений для очевидности Тьюринг-полноты языка Pascal.
C
В языке C нет высокоуровневого понятия переменной (в смысле Паскаля), есть объекты (object), хранящиеся в памяти как последовательно расположенные байты,имеющие адрес (байты в свою очередь состоят из неадресуемых битов). Целые типы ограничены (конечное множество значений), указатель отождествляется с адресом, постулируется возможность хранить адрес в целочисленной переменной (int или long — зависит от реализации), откуда следует ограниченность множества значений указателей, а стало быть, и ограниченность адресного пространства C-машины. То есть язык C, как и язык ассемблера, ориентирован на архитектуру с конечной памятью. Файл не является типом данных языка C, в отличие от Паскаля. Это вещь из окружения, для работы с которой есть операции над потоками в виде набора библиотечных функций. Тип fpos_t, принятый в стандарте C для позиционирования файлов, постулируется как «отличный от массива тип данных (object type)». Следовательно, множество значений этого типа конечно, а значит, максимальная длина файла в языке C ограничена сверху.
SQL
Сам по себе SQL никогда не считался полным по Тьюрингу языком. Однако, у него существует множество расширений, позволяющих делать рекурсивные запросы, циклы, списки, деревья и пр., например, с помощью PostgreSQL[2]. Более того, на в 2011 г. Habrahabr появилась статья, где показана машина Тьюринга на SQL[3] (в реализации Firebird 2.1, который ограничивает вложенность рекурсивных запросов до 2014 уровней). Тем не менее, всё ещё остаётся ограниченное query execution time.
HTML
HTML можно назвать языком программирования только в контексте формальной полемики. На деле он является языком гипертекстовой разметки и ни чем больше. Т. е. на HTML можно совершить только некоторую ограниченную совокупность действий, интерпретируемых браузером, однако никто не запрещает сделать язык, идентичный по синтаксису с HTML, но интерпретируемый совершенно по другому таким образом, чтобы он был полным по Тьюрингу.
Некоторые другие ЯП
| Название языка | Год изобретения | Парадигма | Уровень | Зависимость от архитектуры процессора | Полнота по Тьюрингу |
|---|---|---|---|---|---|
| C | 1972 | Процедурный | Низкий | зав. от ISO | Да |
| C++ | 1983 | Мультипарадигменный | Высокий/Низкий | Нет | Да |
| Язык Ассемблера | 1950 | Полнофункциональный | Низкий | Да | Да |
| SQL | 1989 | Декларативный | Высокий | Нет | Нет |
| Haskell | 1990 | Функциональный | Высокий | Нет | Да |
| HTML | 1986 | Декларативный | Высокий | Нет | Нет |
| CSS | 1996 | Декларативный | Высокий | Нет | Нет |
| Java | 1995 | Объектно-ориентированный | Высокий | Нет | Да |
| JavaScript | 1995 | Объектно-ориентированный | Высокий | Нет | Да |
| Python | 1991 | Объектно-ориентированный | Высокий | Нет | Да |
| XML | 1998 | Декларативный | Высокий | Нет | Нет |
| Brainfuck | 1993 | Эзотерический | Низкий | Да | Да |
| Whitespace | 2003 | Эзотерический | Низкий | Да | Да |
Интересные случаи полноты по Тьюрингу
Шаблоны C++
Шаблоны C++ позволяют производить сложные вычисления ещё на стадии компиляции программы. Впервые это было продемонстрировано Эрвином Унрухом, который реализовал рекурсивный алгоритм распознавания простых чисел в процессе компиляции. Позже в статье Университета Индиана было продемонстрировано кодирование машины Тьюринга в шаблонах C++[4].
Java Generics
Аналогично C++ Templates, Generics, несмотря на свои отличия, тоже оказались полными по Тьюрингу, что было подтверждено Раду Григор в одной из статей Кентского Университета[5].
URISC
URISC (от англ. Ultimate RISC) — предельный случай процессора типа RISC (буквально: компьютер с предельно сокращённым набором инструкций), который умеет выполнять одну-единственную инструкцию. Обычно это «вычесть и пропустить следующую инструкцию, если вычитаемое было больше уменьшаемого» (англ. «reverse-subtract and skip if borrow»). Аналогичная концепция, основанная именно на «вычесть и перейти, если результат не положительный» (англ. «subtract and branch unless positive»), называется SUBLEQ.
URISC также известен в современной литературе как OISC (англ. One Instruction Set Computer) и является полным по Тьюрингу.
mov
Утилита M/o/Vfuscator превращает любую программу на языке C в огромную последовательность из инструкций [6].
HTML5 + CSS3
Нововведения новых версий HTML/CSS позволяют построить[7] правило 110, которое является Тьюринг-полным.
Excel
Excel имеет свой скриптовый язык. Однако, для кодирования Машины Тьюринга в таблице Excel достаточно использование только формул[8].
Тьюринг-полнота в играх
- Minecraft[9]. Возможно, достижение Тьюринг-полноты в игре-песочнице с возможностью создания логических элементов было неизбежным, но сложность компьютеров, собираемых из блоков в данной игре, достойна внимания.
- Little Big Planet[10]. Некоторые элементы игры представляют из себя ничто иное, как небольшие клеточные автоматы, которые можно запрограммировать.
- Super Mario World[11]. Умелое обращение с багами игры позволяет сделать в ней буквально всё, что позволяет 2d-пространство Nintendo.
Тьюринговская трясина
Тьюринговская трясина — жаргонное общее название для языков программирования, которые Тьюринг-полны, но обладают крайне примитивными синтаксисом и семантикой. Они неудобны для практического программирования (из-за трудности написания программ и низкой производительности), зато хорошо подходят для некоторых других задач (доказательство невычислимости некоторых функций, иллюстрация базовых принципов программирования и т. д.). Поэтому они интересны для информатики.
Первыми представителями «трясины» были лямбда-исчисление, комбинаторная логика и сама машина Тьюринга.
Многие эзотерические языки программирования также являются «трясинами Тьюринга» (напр. Brainfuck, Spoon, Malbolge, Whitespace).
Проблема остановки
| Определение: |
| Проблема остановки — проблема определения факта остановки данной машины Тьюринга на данных входных данных (закончит выполнение или нет). |
| Теорема: |
Проблема остановки неразрешима |
| Доказательство: |
|
Докажем от противного. Предположим существует такая полностью вычислимая функция , которая возвращает , если функция остановится когда-либо, и , если функция никогда не остановится. Рассмотрим следующую функцию void g():
if halts(g):
for(;;)
должна возвращать либо , либо .
|
Теорема Геделя о неполноте
Чтобы доказать теорему, можно воспользоваться проблемой остановки машины Тьюринга.
| Теорема: |
Любая непротиворечивая формальная система аксиом , способная выражать утверждения о натуральных числах и доказывать простые арифметические факты, неполна — существуют утверждения о натуральных числах, которые она не может ни доказать, ни опровергнуть. |
| Доказательство: |
|
См. также
Примечания
- ↑ Википедия — Формальный язык
- ↑ High Performance with PostgreSQL 8.4
- ↑ Тьюринга на чистом SQL
- ↑ C++ Templates are Turing-complete
- ↑ Java Generics are Turing-complete
- ↑ M/o/Vfuscator
- ↑ Rule 110
- ↑ Excel Turing Machine
- ↑ the CPU. Then coughing a lot. Sorry about that. I may be dying.
- ↑ LittleBigLife — The Game of Life in LittleBigPlanet
- ↑ SNES Code Injection -- Flappy Bird in SMW