Невозможность византийского консенсуса — различия между версиями
Yeputons (обсуждение | вклад) (Новая страница: «Можно доказать, например, что при ''n'' = 3, ''f'' = 1 консенсус Проблема византийских генерало…») |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 4 промежуточные версии 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | Можно доказать, например, что при ''n'' = 3, ''f'' = 1 консенсус [[Проблема византийских генералов|византийских генералов]] невозможен. | + | [[Категория: Параллельное программирование]] |
| + | Можно доказать, например, что при ''n'' = 3, ''f'' = 1 (три процесса, из них один византийский) консенсус [[Проблема византийских генералов|византийских генералов]] невозможен. | ||
Доказательство от Елизарова: | Доказательство от Елизарова: | ||
| − | Пусть каждому процессу подаётся число 0 или 1 на вход(могут быть разными на разных процессах). Задача - прийти к нетривиальному консенсусу всем работающим процессам на одном значении, которое было дано на вход хотя бы одному | + | Пусть каждому процессу подаётся число 0 или 1 на вход (могут быть разными на разных процессах). Задача - прийти к нетривиальному обоснованному консенсусу всем работающим процессам на одном значении, которое было дано на вход хотя бы одному невизантийскому процессу. |
| − | + | Предположим обратное. Пусть существует алгоритм консенсуса. Тогда алгоритм — это код, которому требуется дать два канала связи с оставшимися двумя процессами. | |
| + | Сделаем страшное и странное: запустим 4 процесса с этим алгоритмом так, как на картинке, и подадим верхним на вход 0, а нижним — 1. | ||
| + | Они будут как-то работать, посмотри, к какому выводу могут прийти эти процессы (если вообще придут). | ||
| − | + | [[Файл:byzantine.png]] | |
| − | + | Посмотрим на картинку одним способом: как будто два верхних процесса — это обычные процессы, а нижняя половина — это византийских процесс (у него два канала связи с нормальными, он внутри что-то как-то делает и с ними общается, выдавая чушь). | |
| + | Тогда верхние процессы обязаны независимо от происходящего в нижней половине прийти к консенсусу на 0. | ||
| + | Аналогично, если считать 2 нижних процесса рабочими, а 2 верхних — одним сбойным, то нижние приходят к консенсусу на 1. | ||
| + | То есть все процессы завершились и посчитали, что консенсус есть. | ||
| + | |||
| + | А теперь если мы считаем рабочими 2 правых, а 2 левых — одним сбойным (ведущим себя как пара из верхнего рабочего и нижнего рабочего), то два правых должны прийти к консенсусу. | ||
| + | Но вместо этого верхний правый придет к консенсусу на 0 вместе с воображаемым верхним соседом, а нижний правый — к консенсусу на 1 с воображаемым нижним соседом. | ||
| + | Противоречие. | ||
Поэтому такого алгоритма нет, и консенсус при N=3 и f=1 невозможен. | Поэтому такого алгоритма нет, и консенсус при N=3 и f=1 невозможен. | ||
Текущая версия на 19:43, 4 сентября 2022
Можно доказать, например, что при n = 3, f = 1 (три процесса, из них один византийский) консенсус византийских генералов невозможен.
Доказательство от Елизарова:
Пусть каждому процессу подаётся число 0 или 1 на вход (могут быть разными на разных процессах). Задача - прийти к нетривиальному обоснованному консенсусу всем работающим процессам на одном значении, которое было дано на вход хотя бы одному невизантийскому процессу.
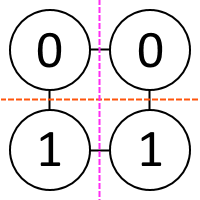
Предположим обратное. Пусть существует алгоритм консенсуса. Тогда алгоритм — это код, которому требуется дать два канала связи с оставшимися двумя процессами. Сделаем страшное и странное: запустим 4 процесса с этим алгоритмом так, как на картинке, и подадим верхним на вход 0, а нижним — 1. Они будут как-то работать, посмотри, к какому выводу могут прийти эти процессы (если вообще придут).
Посмотрим на картинку одним способом: как будто два верхних процесса — это обычные процессы, а нижняя половина — это византийских процесс (у него два канала связи с нормальными, он внутри что-то как-то делает и с ними общается, выдавая чушь). Тогда верхние процессы обязаны независимо от происходящего в нижней половине прийти к консенсусу на 0. Аналогично, если считать 2 нижних процесса рабочими, а 2 верхних — одним сбойным, то нижние приходят к консенсусу на 1. То есть все процессы завершились и посчитали, что консенсус есть.
А теперь если мы считаем рабочими 2 правых, а 2 левых — одним сбойным (ведущим себя как пара из верхнего рабочего и нижнего рабочего), то два правых должны прийти к консенсусу. Но вместо этого верхний правый придет к консенсусу на 0 вместе с воображаемым верхним соседом, а нижний правый — к консенсусу на 1 с воображаемым нижним соседом. Противоречие.
Поэтому такого алгоритма нет, и консенсус при N=3 и f=1 невозможен.