Рекурсивные нейронные сети — различия между версиями
(→Описание) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 37 промежуточных версий 5 участников) | |||
| Строка 1: | Строка 1: | ||
| − | Рекурсивная нейронная | + | Рекурсивная нейронная сеть {{---}} тип глубокой нейронной сети, сформированный при применении одних и тех же наборов весов рекурсивно через структуру в виде дерева, чтобы сделать скалярное или структурированное предсказание над входными данными переменного размера через обход дерева в топологическом порядке.<ref name=definition>[https://neurohive.io/ru/osnovy-data-science/7-arhitektur-nejronnyh-setej-nlp/ 7 архитектур нейронных сетей для решения задач NLP]</ref> |
==Применение== | ==Применение== | ||
| − | Модели рекурсивных сетей используют иерархические структуры образцов при обучении | + | Модели рекурсивных сетей используют иерархические структуры образцов при обучении, поэтому они преуспели в следующих областях: |
| − | + | *Обработка естественного языка. Модели используются для предсказания тональности предложения <ref name=Socher>[https://www-nlp.stanford.edu/pubs/SocherLinNgManning_ICML2011.pdf Richard Socher, Cliff Chiung-Yu Lin, Andrew Y. Ng, Christopher D. Manning. Parsing Natural Scenes and Natural Language with Recursive Neural Networks]</ref>: | |
| − | *Обработка естественного языка. | + | [[File:NLP via RvNN.png|400px|frameless]] |
| − | *Обработка изображений с природными ландшафтами | + | *Обработка изображений с природными ландшафтами<ref name=Socher2>[https://www-nlp.stanford.edu/pubs/SocherLinNgManning_ICML2011.pdf Richard Socher, Cliff Chiung-Yu Lin, Andrew Y. Ng, Christopher D. Manning. Parsing Natural Scenes and Natural Language with Recursive Neural Networks]</ref>. |
| + | [[File:Parsing Natural Scenes Images RvNN.png|500px|frameless]] | ||
==Описание== | ==Описание== | ||
| − | [[Файл: | + | [[Файл:JBw4cyCl4yE.jpg|thumbnail|[http://cs224d.stanford.edu/lectures/CS224d-Lecture10.pdf Архитектура простой рекурсивной сети]]] |
| − | + | При обучении последовательных структур и деревьев в задачах обработки естественного языка, фразы и предложения моделируются через векторное представление слов. | |
| − | Базовая структура сети является бинарным деревом, состоящим из родительского компонента ( | + | Базовая структура сети является бинарным деревом, состоящим из родительского компонента (корня), и дочерних компонентов (листьев). Каждый компонент - набор нейронов, размер которого зависит от сложности входных данных. Входная последовательность данных подаётся на листья, а корень использует классификатор для определения класса и меры (score) |
Рекурсивная нейронная сеть использует следующую формулу для вычисления родительского вектора: | Рекурсивная нейронная сеть использует следующую формулу для вычисления родительского вектора: | ||
| − | <math>p_{1 | + | <math>p_{1} = f\left(W[b ; c]+ bias\right)</math> |
| − | + | *<math>b, c</math> {{---}} дочерние векторы | |
| − | + | *<math>W</math> {{---}} обученная матрица весов, <math>W \in R^{d \times 2d}</math> | |
| − | f - нелинейную функция активации типа гиперболического тангенса | + | *<math>f</math> {{---}} нелинейную функция активации типа гиперболического тангенса |
| − | + | *<math>bias</math> - cмещение, оно может быть добавлено в качестве дополнительного столбца к <math>W</math>, если к конкатенации входных векторов добавляется 1. | |
| + | Родительские векторы должны иметь одинаковую размерность, чтобы быть рекурсивно совместимыми и использоваться в качестве входных данных для следующей композиции. | ||
| − | + | Последующие шаги получают на вход меру предыдущего корня и следующее слово последовательности, таким образом пока в сети не будет сформировано дерево со всеми словами в последовательности. | |
| − | Мера дерева - сумма мер на каждом узле | + | Деревья могут иметь разную структуру, выбор лучшей подструктуры дерева для сети основывается на их мере. Мера дерева - сумма мер на каждом узле: |
| − | После выбора структуры сеть классифицирует части последовательности. Вероятность принадлежности к классу вектора p вычисляется классификатором с помощью функции Softmax. | + | <math>s(x,y) = \sum\limits_{n \in nodes(y)}s_n</math> |
| + | |||
| + | После выбора структуры, сеть классифицирует части последовательности. Вероятность принадлежности к классу вектора p вычисляется классификатором с помощью функции Softmax: | ||
| + | |||
| + | <math>label_{p} = softmax(W^{label}p)</math> | ||
| + | |||
| + | Здесь <math>W^{label}</math> {{---}} матрица классификаций. Основной задачей и разницей между моделями будет вычисление скрытых векторов <math>p_i\in R^{d}</math> снизу вверх. | ||
| + | |||
| + | ===Алгоритм обратного распространения ошибки=== | ||
| + | В рекурсивных нейронных сетях используется [[:Обратное_распространение_ошибки|алгоритм обратного распространения ошибки (backpropagation)]] с некоторыми отличиями, вытекающими из древовидной структуры и рекурсии: | ||
| + | * Сумма производных матрицы W от всех узлов. Можно предположить, что она разная на каждом узле, однако если взять отдельные производные от каждого вхождения, то получится то же самое. | ||
| + | * Разделение производных в каждом узле. Во время прямого распространения, родительский вектор считается через дочерние узлы по формуле выше. Следовательно, ошибки должны быть вычислены относительно каждого из них, причём ошибка каждого дочернего узла является n-мерной | ||
=Рекурсивные и рекуррентные нейронные сети= | =Рекурсивные и рекуррентные нейронные сети= | ||
[[File:RNN.png|450px|thumb|[http://colah.github.io/posts/2015-08-Understanding-LSTMs/ RNN и ее развернутое представление]]] | [[File:RNN.png|450px|thumb|[http://colah.github.io/posts/2015-08-Understanding-LSTMs/ RNN и ее развернутое представление]]] | ||
| − | Рекуррентная нейронная сеть представляет собой рекурсивную сеть со специфической структурой - в виде линейной цепочки. Рекурсивные сети работают на структурах общего типа, включающих иерархию, рекуррентные сети работают исключительно на линейной прогрессии во времени, связывая предыдущий момент времени со следующим через скрытый нейронный слой . | + | Рекуррентная нейронная сеть представляет собой рекурсивную сеть со специфической структурой - в виде линейной цепочки. Рекурсивные сети работают на структурах общего типа, включающих иерархию, рекуррентные сети работают исключительно на линейной прогрессии во времени, связывая предыдущий момент времени со следующим через скрытый нейронный слой.<ref name=RNN>[https://ru.wikipedia.org/wiki/Рекурсивные_нейронные_сети Рекурсивные нейронные сети. Википедия]</ref> |
==Примеры кода== | ==Примеры кода== | ||
| + | [[File:Rntn-layer.png|450px|thumb| Визуализация тензорной нейронной сети]] | ||
| + | |||
| + | Опишем здесь пример построения сети, опустив построение дерева. | ||
| + | [https://github.com/yc930401/RecNN-pytorch Полный листинг кода для анализа тональности текста на PyTorch] (из статьи [https://nlp.stanford.edu/~socherr/EMNLP2013_RNTN.pdf Socher et al.(2013c)]) | ||
| + | |||
| + | class RNTN(nn.Module): | ||
| + | def __init__(self, word2index, hidden_size, output_size): | ||
| + | super(RNTN,self).__init__() | ||
| + | <font color="green"># Для рекурсивной нейронной сети обязательно нужно для векторное представление слов</font> | ||
| + | self.word2index = word2index | ||
| + | self.embed = nn.Embedding(len(word2index), hidden_size) | ||
| + | self.V = nn.ParameterList([nn.Parameter(torch.randn(hidden_size * 2, hidden_size * 2)) for _ in range(hidden_size)]) <font color="green"># Тензор</font> | ||
| + | self.W = nn.Parameter(torch.randn(hidden_size * 2, hidden_size)) | ||
| + | self.b = nn.Parameter(torch.randn(1, hidden_size)) <font color="green"># bias</font> | ||
| + | self.W_out = nn.Linear(hidden_size, output_size) | ||
| + | |||
| + | <font color="green"># инициализация весов</font> | ||
| + | def init_weight(self): | ||
| + | nn.init.xavier_uniform(self.embed.state_dict()['weight']) | ||
| + | nn.init.xavier_uniform(self.W_out.state_dict()['weight']) | ||
| + | for param in self.V.parameters(): | ||
| + | nn.init.xavier_uniform(param) | ||
| + | nn.init.xavier_uniform(self.W) | ||
| + | self.b.data.fill_(0) | ||
| + | |||
| + | <font color="green"># прямое распространение</font> | ||
| + | def tree_propagation(self, node): | ||
| + | recursive_tensor = OrderedDict() | ||
| + | current = None | ||
| + | if node.isLeaf: | ||
| + | tensor = Variable(LongTensor([self.word2index[node.word]])) if node.word in self.word2index.keys() \ | ||
| + | else Variable(LongTensor([self.word2index['<UNK>']])) | ||
| + | current = self.embed(tensor) # 1xD | ||
| + | else: | ||
| + | recursive_tensor.update(self.tree_propagation(node.left)) | ||
| + | recursive_tensor.update(self.tree_propagation(node.right)) | ||
| + | |||
| + | concated = torch.cat([recursive_tensor[node.left], recursive_tensor[node.right]], 1) <font color="green"># 1x2D</font> | ||
| + | xVx = [] | ||
| + | for i, v in enumerate(self.V): | ||
| + | xVx.append(torch.matmul(torch.matmul(concated, v), concated.transpose(0, 1))) | ||
| + | xVx = torch.cat(xVx, 1) # 1xD | ||
| + | Wx = torch.matmul(concated, self.W) # 1xD | ||
| + | current = F.tanh(xVx + Wx + self.b) # 1xD | ||
| + | recursive_tensor[node] = current | ||
| + | return recursive_tensor | ||
| + | |||
| + | def forward(self, Trees, root_only=False): | ||
| + | propagated = [] | ||
| + | if not isinstance(Trees, list): | ||
| + | Trees = [Trees] | ||
| + | |||
| + | for Tree in Trees: | ||
| + | recursive_tensor = self.tree_propagation(Tree.root) | ||
| + | if root_only: | ||
| + | recursive_tensor = recursive_tensor[Tree.root] | ||
| + | propagated.append(recursive_tensor) | ||
| + | else: | ||
| + | recursive_tensor = [tensor for node,tensor in recursive_tensor.items()] | ||
| + | propagated.extend(recursive_tensor) | ||
| + | |||
| + | propagated = torch.cat(propagated) # (num_of_node in batch, D) | ||
| + | |||
| + | return F.log_softmax(self.W_out(propagated),1) | ||
| + | |||
| + | ===Обучение=== | ||
| + | |||
| + | HIDDEN_SIZE = 30 | ||
| + | BATCH_SIZE = 20 | ||
| + | EPOCH = 20 | ||
| + | LR = 0.01 | ||
| + | LAMBDA = 1e-5 | ||
| + | RESCHEDULED = False | ||
| + | for epoch in range(EPOCH): | ||
| + | losses = [] | ||
| + | <font color="green"># learning rate annealing</font> | ||
| + | if RESCHEDULED == False and epoch == EPOCH // 2: | ||
| + | LR *= 0.1 | ||
| + | optimizer = optim.Adam(model.parameters(), lr=LR, weight_decay=LAMBDA) <font color="green"># L2 нормализация</font> | ||
| + | RESCHEDULED = True | ||
| + | for i, batch in enumerate(getBatch(BATCH_SIZE, train_data)): | ||
| + | if ROOT_ONLY: | ||
| + | labels = [tree.labels[-1] for tree in batch] | ||
| + | labels = Variable(LongTensor(labels)) | ||
| + | else: | ||
| + | labels = [tree.labels for tree in batch] | ||
| + | labels = Variable(LongTensor(flatten(labels))) | ||
| + | model.zero_grad() | ||
| + | preds = model(batch, ROOT_ONLY) | ||
| + | loss = loss_function(preds, labels) | ||
| + | losses.append(loss.data.tolist()[0]) | ||
| + | loss.backward() | ||
| + | optimizer.step() | ||
| + | if i % 100 == 0: | ||
| + | print('[%d/%d] mean_loss : %.2f' % (epoch, EPOCH, np.mean(losses))) | ||
| + | losses = [] | ||
| + | |||
| + | |||
Примеры кода на TensorFlow: | Примеры кода на TensorFlow: | ||
*https://github.com/bogatyy/cs224d/tree/master/assignment3 | *https://github.com/bogatyy/cs224d/tree/master/assignment3 | ||
| Строка 45: | Строка 156: | ||
== Cм. также == | == Cм. также == | ||
*[[:Рекуррентные_нейронные_сети|Рекуррентные нейронные сети]] | *[[:Рекуррентные_нейронные_сети|Рекуррентные нейронные сети]] | ||
| − | *https://nlp.stanford.edu/~socherr/EMNLP2013_RNTN.pdf | + | |
| − | *http://cs224d.stanford.edu/lectures/CS224d-Lecture10.pdf | + | == Примечания == |
| + | <references /> | ||
| + | |||
| + | == Источники == | ||
| + | *[https://nlp.stanford.edu/~socherr/EMNLP2013_RNTN.pdf] - Richard Socher, Alex Perelygin, Jean Y. Wu, Jason Chuang, Christopher D. Manning, Andrew Y. Ng, Christopher Potts. Recursive Deep Models for Semantic Compositionality Over a Sentiment Treebank. Stanford University, Stanford | ||
| + | *[http://cs224d.stanford.edu/lectures/CS224d-Lecture10.pdf] - Richard Socher. Wrap up: LSTMs and Recursive Neural Networks | ||
| + | *[https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D0%BA%D1%83%D1%80%D1%81%D0%B8%D0%B2%D0%BD%D1%8B%D0%B5_%D0%BD%D0%B5%D0%B9%D1%80%D0%BE%D0%BD%D0%BD%D1%8B%D0%B5_%D1%81%D0%B5%D1%82%D0%B8] - Рекурсивные нейронные сети. Википедия | ||
| + | |||
| + | [[Категория: Машинное обучение]] [[Категория: Нейронные сети]] | ||
Текущая версия на 19:43, 4 сентября 2022
Рекурсивная нейронная сеть — тип глубокой нейронной сети, сформированный при применении одних и тех же наборов весов рекурсивно через структуру в виде дерева, чтобы сделать скалярное или структурированное предсказание над входными данными переменного размера через обход дерева в топологическом порядке.[1]
Содержание
Применение
Модели рекурсивных сетей используют иерархические структуры образцов при обучении, поэтому они преуспели в следующих областях:
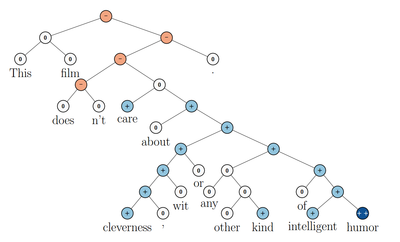
- Обработка естественного языка. Модели используются для предсказания тональности предложения [2]:
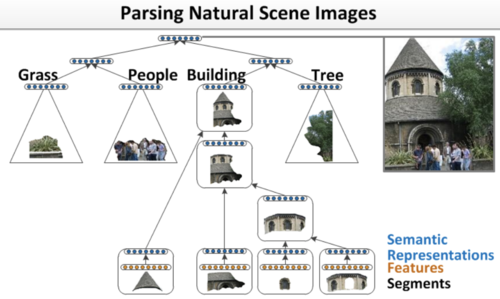
- Обработка изображений с природными ландшафтами[3].
Описание
При обучении последовательных структур и деревьев в задачах обработки естественного языка, фразы и предложения моделируются через векторное представление слов.
Базовая структура сети является бинарным деревом, состоящим из родительского компонента (корня), и дочерних компонентов (листьев). Каждый компонент - набор нейронов, размер которого зависит от сложности входных данных. Входная последовательность данных подаётся на листья, а корень использует классификатор для определения класса и меры (score)
Рекурсивная нейронная сеть использует следующую формулу для вычисления родительского вектора:
- — дочерние векторы
- — обученная матрица весов,
- — нелинейную функция активации типа гиперболического тангенса
- - cмещение, оно может быть добавлено в качестве дополнительного столбца к , если к конкатенации входных векторов добавляется 1.
Родительские векторы должны иметь одинаковую размерность, чтобы быть рекурсивно совместимыми и использоваться в качестве входных данных для следующей композиции.
Последующие шаги получают на вход меру предыдущего корня и следующее слово последовательности, таким образом пока в сети не будет сформировано дерево со всеми словами в последовательности.
Деревья могут иметь разную структуру, выбор лучшей подструктуры дерева для сети основывается на их мере. Мера дерева - сумма мер на каждом узле:
После выбора структуры, сеть классифицирует части последовательности. Вероятность принадлежности к классу вектора p вычисляется классификатором с помощью функции Softmax:
Здесь — матрица классификаций. Основной задачей и разницей между моделями будет вычисление скрытых векторов снизу вверх.
Алгоритм обратного распространения ошибки
В рекурсивных нейронных сетях используется алгоритм обратного распространения ошибки (backpropagation) с некоторыми отличиями, вытекающими из древовидной структуры и рекурсии:
- Сумма производных матрицы W от всех узлов. Можно предположить, что она разная на каждом узле, однако если взять отдельные производные от каждого вхождения, то получится то же самое.
- Разделение производных в каждом узле. Во время прямого распространения, родительский вектор считается через дочерние узлы по формуле выше. Следовательно, ошибки должны быть вычислены относительно каждого из них, причём ошибка каждого дочернего узла является n-мерной
Рекурсивные и рекуррентные нейронные сети
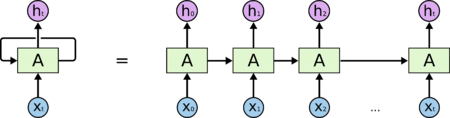
Рекуррентная нейронная сеть представляет собой рекурсивную сеть со специфической структурой - в виде линейной цепочки. Рекурсивные сети работают на структурах общего типа, включающих иерархию, рекуррентные сети работают исключительно на линейной прогрессии во времени, связывая предыдущий момент времени со следующим через скрытый нейронный слой.[4]
Примеры кода
Опишем здесь пример построения сети, опустив построение дерева. Полный листинг кода для анализа тональности текста на PyTorch (из статьи Socher et al.(2013c))
class RNTN(nn.Module):
def __init__(self, word2index, hidden_size, output_size):
super(RNTN,self).__init__()
# Для рекурсивной нейронной сети обязательно нужно для векторное представление слов
self.word2index = word2index
self.embed = nn.Embedding(len(word2index), hidden_size)
self.V = nn.ParameterList([nn.Parameter(torch.randn(hidden_size * 2, hidden_size * 2)) for _ in range(hidden_size)]) # Тензор
self.W = nn.Parameter(torch.randn(hidden_size * 2, hidden_size))
self.b = nn.Parameter(torch.randn(1, hidden_size)) # bias
self.W_out = nn.Linear(hidden_size, output_size)
# инициализация весов
def init_weight(self):
nn.init.xavier_uniform(self.embed.state_dict()['weight'])
nn.init.xavier_uniform(self.W_out.state_dict()['weight'])
for param in self.V.parameters():
nn.init.xavier_uniform(param)
nn.init.xavier_uniform(self.W)
self.b.data.fill_(0)
# прямое распространение
def tree_propagation(self, node):
recursive_tensor = OrderedDict()
current = None
if node.isLeaf:
tensor = Variable(LongTensor([self.word2index[node.word]])) if node.word in self.word2index.keys() \
else Variable(LongTensor([self.word2index['<UNK>']]))
current = self.embed(tensor) # 1xD
else:
recursive_tensor.update(self.tree_propagation(node.left))
recursive_tensor.update(self.tree_propagation(node.right))
concated = torch.cat([recursive_tensor[node.left], recursive_tensor[node.right]], 1) # 1x2D
xVx = []
for i, v in enumerate(self.V):
xVx.append(torch.matmul(torch.matmul(concated, v), concated.transpose(0, 1)))
xVx = torch.cat(xVx, 1) # 1xD
Wx = torch.matmul(concated, self.W) # 1xD
current = F.tanh(xVx + Wx + self.b) # 1xD
recursive_tensor[node] = current
return recursive_tensor
def forward(self, Trees, root_only=False):
propagated = []
if not isinstance(Trees, list):
Trees = [Trees]
for Tree in Trees:
recursive_tensor = self.tree_propagation(Tree.root)
if root_only:
recursive_tensor = recursive_tensor[Tree.root]
propagated.append(recursive_tensor)
else:
recursive_tensor = [tensor for node,tensor in recursive_tensor.items()]
propagated.extend(recursive_tensor)
propagated = torch.cat(propagated) # (num_of_node in batch, D)
return F.log_softmax(self.W_out(propagated),1)
Обучение
HIDDEN_SIZE = 30
BATCH_SIZE = 20
EPOCH = 20
LR = 0.01
LAMBDA = 1e-5
RESCHEDULED = False
for epoch in range(EPOCH):
losses = []
# learning rate annealing
if RESCHEDULED == False and epoch == EPOCH // 2:
LR *= 0.1
optimizer = optim.Adam(model.parameters(), lr=LR, weight_decay=LAMBDA) # L2 нормализация
RESCHEDULED = True
for i, batch in enumerate(getBatch(BATCH_SIZE, train_data)):
if ROOT_ONLY:
labels = [tree.labels[-1] for tree in batch]
labels = Variable(LongTensor(labels))
else:
labels = [tree.labels for tree in batch]
labels = Variable(LongTensor(flatten(labels)))
model.zero_grad()
preds = model(batch, ROOT_ONLY)
loss = loss_function(preds, labels)
losses.append(loss.data.tolist()[0])
loss.backward()
optimizer.step()
if i % 100 == 0:
print('[%d/%d] mean_loss : %.2f' % (epoch, EPOCH, np.mean(losses)))
losses = []
Примеры кода на TensorFlow:
- https://github.com/bogatyy/cs224d/tree/master/assignment3
- https://gist.github.com/anj1/504768e05fda49a6e3338e798ae1cddd
Cм. также
Примечания
- ↑ 7 архитектур нейронных сетей для решения задач NLP
- ↑ Richard Socher, Cliff Chiung-Yu Lin, Andrew Y. Ng, Christopher D. Manning. Parsing Natural Scenes and Natural Language with Recursive Neural Networks
- ↑ Richard Socher, Cliff Chiung-Yu Lin, Andrew Y. Ng, Christopher D. Manning. Parsing Natural Scenes and Natural Language with Recursive Neural Networks
- ↑ Рекурсивные нейронные сети. Википедия
Источники
- [1] - Richard Socher, Alex Perelygin, Jean Y. Wu, Jason Chuang, Christopher D. Manning, Andrew Y. Ng, Christopher Potts. Recursive Deep Models for Semantic Compositionality Over a Sentiment Treebank. Stanford University, Stanford
- [2] - Richard Socher. Wrap up: LSTMs and Recursive Neural Networks
- [3] - Рекурсивные нейронные сети. Википедия