Неравенство Крафта — различия между версиями
(Новая страница: «== Предварительные определения == Пусть заданы два произвольных конечных множества, которы...») |
м (rollbackEdits.php mass rollback) |
||
| (не показано 88 промежуточных версий 6 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
| − | |||
| − | + | Рассматриваемое ниже неравенство Крафта показывает для каких длин кодовых слов существует префиксный код. | |
| − | + | {{Теорема | |
| + | |about=неравенство Крафта | ||
| + | |statement= | ||
| + | Пусть у нас есть <tex>n</tex> [[Основные определения, связанные со строками|символов]], кодовые слова которых имеют длины <tex>l_1 \leqslant l_2 \leqslant \ldots \leqslant l_n </tex>. | ||
| − | + | Тогда необходимое и достаточное условие существования префиксного кода в <tex>r</tex>-ичном алфавите для данных символов, состоит в выполнении неравенства: | |
| + | |||
| + | <center><tex> \sum\limits_{i = 1}^{n} r ^{-l_i} \leqslant 1 </tex></center> | ||
| + | |||
| + | |proof= | ||
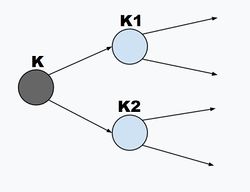
| − | + | [[file:Treeforkraft.jpg|thumb|250px|Иллюстрация к доказательству индукционного перехода]] | |
| − | + | '''Необходимость:''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Напомним, что префиксный код можно представить в виде <tex>r</tex>-ичного корневого дерева, рёбра которого соответствуют символам алфавита, а листья соответствующим кодам. Неравенство Крафта будем доказывать по [[Математическая индукция|индукции]]. | |
| − | |||
| − | + | Для простоты рассмотрим сначала случай двоичного алфавита, то есть <tex>r = 2</tex>. | |
| − | + | '''База:''' Если максимальная длина пути на дереве равна <tex>1</tex>, то в дереве есть одно или два ребра длины <tex>1</tex>. Таким образом, либо <tex> \dfrac{1}{2} \leqslant 1 </tex> — для одного символа источника, либо <tex> \dfrac{1}{2} + \dfrac{1}{2} \leqslant 1 </tex> — для двух символов источника. | |
| − | + | '''Переход:''' Предположим далее, что неравенство Крафта справедливо для всех деревьев высоты меньше <tex>n - 1</tex>. | |
| + | Докажем, что оно справедливо и для всех деревьев высоты меньше <tex>n</tex>. Для данного дерева максимальной высоты <tex>n</tex> ребра из первой вершины ведут к двум поддеревьям, высоты которых не превышают <tex>n - 1</tex>; для этих поддеревьев имеем неравенства <tex>K_1 \leqslant 1</tex> и <tex>K_2 \leqslant 1</tex>, где <tex>K_1, K_2</tex> — значения соответствующих им сумм. Каждая длина <tex>l_i</tex> в поддереве увеличивается на <tex>1</tex>, когда поддерево присоединяется к основному дереву, поэтому возникает дополнительный множитель <tex>\dfrac{1}{2}</tex>. Таким образом, имеем <tex>\dfrac{1}{2} K_1 + \dfrac{1}{2} K_2 \leqslant 1</tex>. | ||
| − | |||
| − | + | В случае произвольного недвоичного основания <tex>r</tex> имеется не более <tex>r</tex> ребер, исходящих из каждой вершины, то есть не более <tex>r</tex> поддеревьев; каждое из них присоединяется к основному дереву, давая дополнительный множитель <tex>\dfrac{1}{r}</tex>. Отсюда снова следует утверждение теоремы. | |
| − | + | '''Достаточность:''' | |
| − | |||
| − | |||
| − | |||
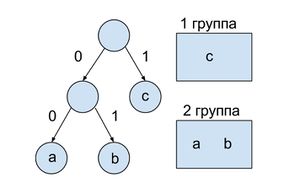
| − | + | [[file:Tree2forkraft.jpg|thumb|300px|Пример разбиения на группы, при <tex> r = 2</tex>, символах ''a, b, c'', где <tex> l_a = 2, l_b = 2, l_c = 1</tex>]] | |
| − | Если на | + | #Если некоторое <tex> l_i = 0 </tex> , то <tex> n = 1 </tex> . В таком случае пустая строка является искомым префиксным кодом. Далее все <tex> l_i \geqslant 1 </tex> . |
| + | #Для доказательства корректности разделим длины <tex> l_i </tex> на <tex>r</tex> , возможно пустых, групп, внутри каждой из которых <tex> \sum\limits r ^{-l_i} \leqslant \dfrac{1}{r} </tex> . | ||
| + | #:Пусть у нас есть <tex>n</tex> символов, кодовые слова имеют длины <tex>l_1 \leqslant l_2 \leqslant \ldots \leqslant l_n </tex>. Давайте разделим данные символы на <tex>r</tex> групп, внутри каждой из которых <tex> \sum\limits r ^{-l_i} \leqslant \dfrac{1}{r} </tex> . Разделить символы на группы можно следующим жадным образом: брать <tex> l_i </tex> в порядке увеличения индекса. | ||
| + | #:Докажем, что в таком случае группа будет либо полностью укомплектована <tex>(\sum\limits r ^{-l_i} = \dfrac{1}{r})</tex>, либо будут исчерпаны все возможные <tex> l_i </tex> . Это следует из того, что при <tex> l_i \geqslant 1 </tex> на <tex>i</tex>-ом шаге либо группа уже укомплектована, либо ее остаток равен: | ||
| + | #: <center><tex> \dfrac{1}{r} - \left ( r^{-l_1} + r^{-l_2} + \ldots + r^{-l_{i-1}} \right ) = \dfrac{r^{l_i-1} - ( r^{l_i - l_1} + r^{l_i - l_2} + \ldots + r^{l_i - l_{i - 1}} )}{r^{l_i}}</tex></center> | ||
| + | #:Так как группа не укомплектована, то числитель положителен. Если добавим <tex> l_i </tex> в группу, то числитель уменьшится на <tex>1</tex>, где <tex>l_i - l_j</tex> неотрицательно при <tex> i \geqslant j </tex> , и <tex> r \in \mathbb{N} </tex>. Следовательно числитель — натуральное число. Тогда, взяв <tex> l_i </tex> в группу, мы не перепрыгнем через максимальное значение, то есть сумма группы <tex> \leqslant \dfrac{1}{r} </tex> . А значит, создавая группы по данному алгоритму мы сможем построить <tex>r</tex> групп, удовлетворяющих условию. | ||
| + | #Выберем для каждой группы свой начальный символ. Запуститим данную процедуру для каждой группы слов, предварительно обрезав первую букву. | ||
| + | #По индукции по величине <tex> l_n </tex> докажем, что наш алгоритм корректен. | ||
| + | #:'''База:''' При <tex> l_n = 0 </tex> корректность процедуры очевидна. | ||
| + | #:'''Переход: ''' Допустим, что процедура корректна для <tex> l_n = w </tex> . Докажем, что процедура корректна и для <tex> l_n = w + 1 </tex> . | ||
| + | #:Заметим, что у слов каждой группы будет своя начальная буква, поэтому достаточно проверить префиксность кода для каждой группы. А это истинно по предположению индукции, где для каждой группы <tex> l_i \leqslant w </tex> . | ||
| − | |||
}} | }} | ||
| − | == | + | == Замечания == |
| − | + | ||
| − | + | Когда имеет место строгое неравенство? Легко заметить, что если любая концевая вершина дерева является кодовым словом, то <tex>K = 1</tex>. Строгое неравенство имеет место лишь в случае, когда некоторые из концевых вершин не используются. Однако, в случае двоичного кодового алфавита какая-нибудь концевая вершина не используется, то предыдущее решение оказывается лишним, и соответствующая цифра может быть удалена из каждого кодового слова, декодирование которого проходит через эту вершину. Таким образом, если имеет место строгое неравенство, то код неэффективен, но для двоичных деревьев очевидно, как можно его улучшить. | |
| − | + | ||
| + | Заметим еще раз, что теорема утверждает существование такого кода и ничего не говорит о конкретных кодах. Может существовать код, который удовлетворяет неравенству Крафта и тем не менее не является префиксным. | ||
| − | == | + | == См.также == |
| − | *[ | + | *[[Неравенство Макмиллана]] |
| − | |||
| − | == | + | == Источники информации == |
| − | * | + | *[http://ru.wikipedia.org/wiki/Неравенство_Крафта Википедия — Неравенство Крафта] |
| + | *[http://books.sernam.ru/book_htc.php?id=35 Неравенство Крафта] | ||
| + | *[https://xlinux.nist.gov/dads/HTML/kraftsinqlty.html Kraft's inequality] | ||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Алгоритмы сжатия]] | [[Категория: Алгоритмы сжатия]] | ||
Текущая версия на 19:43, 4 сентября 2022
Рассматриваемое ниже неравенство Крафта показывает для каких длин кодовых слов существует префиксный код.
| Теорема (неравенство Крафта): |
Пусть у нас есть символов, кодовые слова которых имеют длины .
Тогда необходимое и достаточное условие существования префиксного кода в -ичном алфавите для данных символов, состоит в выполнении неравенства: |
| Доказательство: |
|
Необходимость: Напомним, что префиксный код можно представить в виде -ичного корневого дерева, рёбра которого соответствуют символам алфавита, а листья соответствующим кодам. Неравенство Крафта будем доказывать по индукции. Для простоты рассмотрим сначала случай двоичного алфавита, то есть . База: Если максимальная длина пути на дереве равна , то в дереве есть одно или два ребра длины . Таким образом, либо — для одного символа источника, либо — для двух символов источника. Переход: Предположим далее, что неравенство Крафта справедливо для всех деревьев высоты меньше . Докажем, что оно справедливо и для всех деревьев высоты меньше . Для данного дерева максимальной высоты ребра из первой вершины ведут к двум поддеревьям, высоты которых не превышают ; для этих поддеревьев имеем неравенства и , где — значения соответствующих им сумм. Каждая длина в поддереве увеличивается на , когда поддерево присоединяется к основному дереву, поэтому возникает дополнительный множитель . Таким образом, имеем .
Достаточность:
|
Замечания
Когда имеет место строгое неравенство? Легко заметить, что если любая концевая вершина дерева является кодовым словом, то . Строгое неравенство имеет место лишь в случае, когда некоторые из концевых вершин не используются. Однако, в случае двоичного кодового алфавита какая-нибудь концевая вершина не используется, то предыдущее решение оказывается лишним, и соответствующая цифра может быть удалена из каждого кодового слова, декодирование которого проходит через эту вершину. Таким образом, если имеет место строгое неравенство, то код неэффективен, но для двоичных деревьев очевидно, как можно его улучшить.
Заметим еще раз, что теорема утверждает существование такого кода и ничего не говорит о конкретных кодах. Может существовать код, который удовлетворяет неравенству Крафта и тем не менее не является префиксным.