Деревья Эйлерова обхода — различия между версиями
(→Декартово дерево по неявному ключу) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 4 промежуточные версии 4 участников) | |||
| Строка 26: | Строка 26: | ||
<br> | <br> | ||
| − | Представим дерево в виде последовательности вершин, | + | Представим дерево в виде последовательности вершин, посещенных в порядке эйлерова обхода, начиная с вершины <tex>a</tex>. |
[[Файл:Tour1.png|thumb|320px|center]] | [[Файл:Tour1.png|thumb|320px|center]] | ||
| Строка 61: | Строка 61: | ||
===Проверка на связность=== | ===Проверка на связность=== | ||
| − | Для того, чтобы проверить, лежат ли две вершины в одном дереве, достаточно подняться от вхождения каждой вершины в эйлеров обход (ссылку на которое мы храним) до корня дерева поиска, хранящего этот | + | Для того, чтобы проверить, лежат ли две вершины в одном дереве, достаточно подняться от вхождения каждой вершины в эйлеров обход (ссылку на которое мы храним) до корня дерева поиска, хранящего этот эйлеров обход. |
==Способы реализации структуры== | ==Способы реализации структуры== | ||
| Строка 75: | Строка 75: | ||
Также, можем хранить последовательности вершин эйлерова обхода в [[Декартово_дерево_по_неявному_ключу|декартовом дереве по неявному ключу]]. Глубина декартового дерева, построенного на массиве из <tex>n</tex> вершин, будет поддерживаться равной <tex>O(\log n)</tex>. | Также, можем хранить последовательности вершин эйлерова обхода в [[Декартово_дерево_по_неявному_ключу|декартовом дереве по неявному ключу]]. Глубина декартового дерева, построенного на массиве из <tex>n</tex> вершин, будет поддерживаться равной <tex>O(\log n)</tex>. | ||
| − | Операции объединения и разделения | + | Операции объединения и разделения также выполняются за <tex>O(\log n)</tex>. |
==См. также== | ==См. также== | ||
Текущая версия на 19:44, 4 сентября 2022
Содержание
Задача о динамической связности
| Задача: |
Для динамически изменяющегося дерева выполнить следующие запросы:
|
Для решения поставленной задачи будем представлять дерево в виде его эйлерова графа, а затем будем работать с эйлеровым обходом (англ.Euler tour tree) этого графа. Это позволит выполнять указанные запросы за .
Представление деревьев в виде эйлерова графа
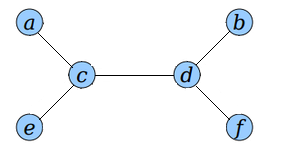
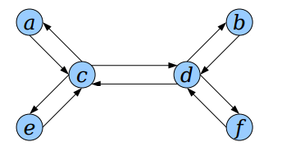
Для представления дерева в виде эйлерового графа заменим каждое ребро дерева на два ребра и .
Получившийся ориентированный граф будет эйлеровым согласно критерию.
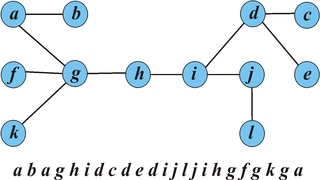
Представим дерево в виде последовательности вершин, посещенных в порядке эйлерова обхода, начиная с вершины .
Операции c эйлеровыми обходами
Добавление ребра
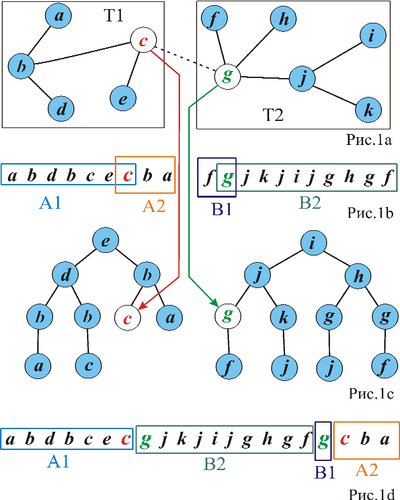
Для добавления ребра :
- Выберем любое вхождение вершины в эйлеров обход дерева .
- Разрежем эйлеров обход на две части:
- — часть обхода до выбранного вхождения вершины , включая ее.
- — часть обхода после выбранного вхождения вершины , включая ее.
- Аналогично, выберем любое вхождение вершины в эйлеров обход дерева и разрежем его на две части и .
- Соберем результирующий эйлеров обход в порядке (без первой повторяющейся вершины), .
Чтобы быстро находить место, где разрезать эйлеровы обходы деревьев и , будем хранить эйлеровы обходы в двоичных деревьях поиска. Ключом вершины для построения дерева поиска будет время посещения этой вершины эйлеровым обходом. Для каждой вершины дерева будем хранить указатель на вершину в дереве поиска, которая соответствует вхождению вершины дерева в эйлеров обход. Тогда за переходим от вершины дерева к вершине дерева поиска, по которой за можно будет разделить дерево поиска на две части.
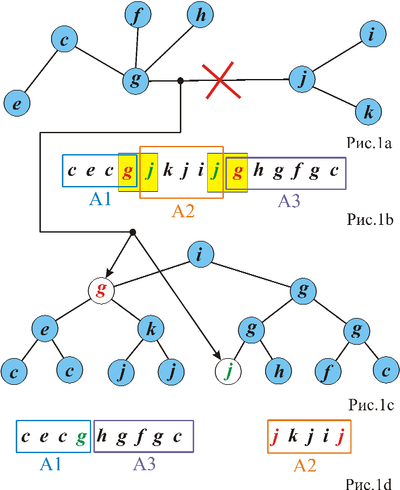
Разрезание ребра
Для удаления ребра :
- Найдем в эйлеровом обходе дерева две пары посещений концов удаляемого ребра и , которые соответствуют прохождениям по ребру в дереве .
- Разрежем эйлеров обход дерева по этим парам на три части: .
- Соединив и (без повторяющейся первой вершины), получим эйлеров обход первого дерева, а дает эйлеров обход второго дерева.
Чтобы быстро находить места в эйлеровом обходе, которые соответствуют прохождению удаляемого ребра в дереве, будем для каждого ребра в дереве хранить ссылку на те места эйлерова обхода, где последовательно посещаем концы удаляемого ребра. Так, для ребра храним ссылки на узлы дерева поиска, соответствующие парам посещений концов этого ребра.
Проверка на связность
Для того, чтобы проверить, лежат ли две вершины в одном дереве, достаточно подняться от вхождения каждой вершины в эйлеров обход (ссылку на которое мы храним) до корня дерева поиска, хранящего этот эйлеров обход.
Способы реализации структуры
Сбалансированное дерево поиска
Будем хранить последовательность вершин эйлерова обхода в виде сбалансированного двоичного дерева поиска, например, в виде красно-черного дерева. При построении дерева ключом вершины будет время посещения этой вершины эйлеровым обходом.
Операции объединения и разделения красно-черных деревьев выполняется за [1].
Декартово дерево по неявному ключу
Также, можем хранить последовательности вершин эйлерова обхода в декартовом дереве по неявному ключу. Глубина декартового дерева, построенного на массиве из вершин, будет поддерживаться равной .
Операции объединения и разделения также выполняются за .