Встречное дерево Фенвика — различия между версиями
Proshev (обсуждение | вклад) |
Proshev (обсуждение | вклад) |
||
| Строка 4: | Строка 4: | ||
}} | }} | ||
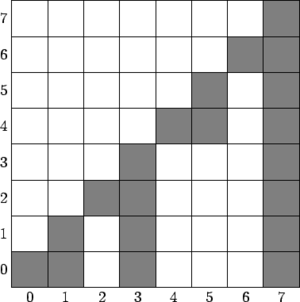
| − | [[Файл:Originalbit.png|thumb | + | [[Файл:Originalbit.png|thumb|Прямое дерево Фенвика]] |
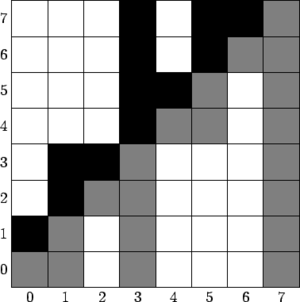
[[Файл:Vstbit.png|thumb|Встречное дерево Фенвика]] | [[Файл:Vstbit.png|thumb|Встречное дерево Фенвика]] | ||
Вспомним, что <tex>h(i)</tex> возвращает количество единиц в двоичной записи числа <tex>i</tex>, а каждый столбец прямого дерево Фенвика вычисляется по формуле <tex>F(i) = \sum_{j=i-2^{h(i)}+1}^i a[j]</tex> | Вспомним, что <tex>h(i)</tex> возвращает количество единиц в двоичной записи числа <tex>i</tex>, а каждый столбец прямого дерево Фенвика вычисляется по формуле <tex>F(i) = \sum_{j=i-2^{h(i)}+1}^i a[j]</tex> | ||
| + | |||
| + | == Свойства == | ||
С помощью встречного дерева Фенвика можно представить любой отрезок от i до j в виде дизъюнктивных объединений отрезков, взятых из прямого и встречного дерева Фенвика. | С помощью встречного дерева Фенвика можно представить любой отрезок от i до j в виде дизъюнктивных объединений отрезков, взятых из прямого и встречного дерева Фенвика. | ||
Версия 03:30, 17 мая 2011
| Определение: |
| Встречное дерево Фенвика — дерево Фенвика, в котором над каждым столбцом идет столбец такой же высоты, вычисляемый по формуле . |
Вспомним, что возвращает количество единиц в двоичной записи числа , а каждый столбец прямого дерево Фенвика вычисляется по формуле
Свойства
С помощью встречного дерева Фенвика можно представить любой отрезок от i до j в виде дизъюнктивных объединений отрезков, взятых из прямого и встречного дерева Фенвика.