Встречное дерево Фенвика — различия между версиями
Proshev (обсуждение | вклад) |
Proshev (обсуждение | вклад) |
||
| Строка 11: | Строка 11: | ||
== Свойства == | == Свойства == | ||
| − | + | Встречное дерево Фенвика - это структура данных, дерево на массиве, обладающее следующими свойствами: | |
| + | |||
| + | 1) позволяет вычислять значение некоторой обратимой операции G на любом отрезке [L; R] за время <tex>O(\log N)</tex>; | ||
| + | |||
| + | 2) позволяет изменять значение любого элемента за <tex>O(\log N)</tex>; | ||
| + | |||
| + | 3) требует <tex>O (N)</tex> памяти, а точнее, ровно столько же, сколько и массив из N элементов; | ||
| + | |||
| + | 4) легко обобщается на случай многомерных массивов. | ||
| + | |||
| + | 5) позволяет представить любой отрезок от i до j в виде дизъюнктивных объединений отрезков, взятых из прямого и встречного дерева Фенвика. | ||
Версия 03:34, 17 мая 2011
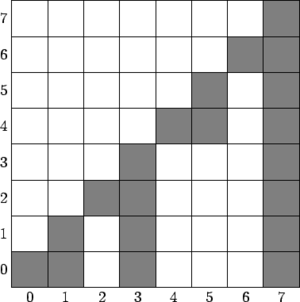
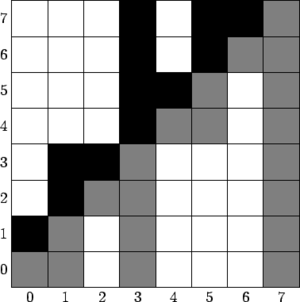
| Определение: |
| Встречное дерево Фенвика — дерево Фенвика, в котором над каждым столбцом идет столбец такой же высоты, вычисляемый по формуле . |
Вспомним, что возвращает количество единиц в двоичной записи числа , а каждый столбец прямого дерево Фенвика вычисляется по формуле
Свойства
Встречное дерево Фенвика - это структура данных, дерево на массиве, обладающее следующими свойствами:
1) позволяет вычислять значение некоторой обратимой операции G на любом отрезке [L; R] за время ;
2) позволяет изменять значение любого элемента за ;
3) требует памяти, а точнее, ровно столько же, сколько и массив из N элементов;
4) легко обобщается на случай многомерных массивов.
5) позволяет представить любой отрезок от i до j в виде дизъюнктивных объединений отрезков, взятых из прямого и встречного дерева Фенвика.