Интерполяционный поиск — различия между версиями
(Новая страница: «Пусть <tex>t</tex> - отсортированный массив чисел из <tex>n</tex> чисел. Тогда можно построить отсорт…») |
|||
| Строка 1: | Строка 1: | ||
| − | + | === Идея === | |
| + | Рассмотрим задачу: найти слово в словаре. Если оно начинается на букву "А", то никто не будет искать его в середине, а откроет словарь ближе к началу. В чем разница между алгоритмом человека и другими? Отличие заключается в том, что алгоритмы вроде двоичного не делают различий между "немного больше" и "существенно больше". | ||
| − | Время работы алгоритма: <tex>O(\log \log n)</tex>. | + | === Алгоритм === |
| + | [[Файл:Search.jpg|thumb|300px|Нахождение медианы]] | ||
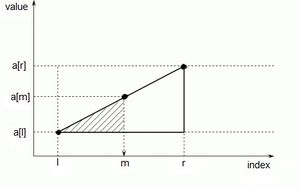
| + | Пусть <tex> a </tex> - отсортированный массив чисел из <tex> n </tex> чисел, <tex> x </tex> - значение, которое нужно найти. | ||
| + | Если известно, что <tex> x </tex> лежит между <tex> a_l </tex> и <tex> a_r </tex>, то следующая проверка выполняется примерно на расстоянии <tex dpi = "180"> \frac{x - a_l}{a_r - a_l} </tex>. | ||
| + | |||
| + | === Время работы === | ||
| + | При условии, что значения элементов близки к арифметической прогрессии, за один шаг алгоритм уменьшает количество проверяемых элементов с <tex> n </tex> до <tex> \sqrt n </tex>. | ||
| + | Поэтому среднее время работы алгоритма: <tex> O(\log \log n) </tex>. | ||
| + | При "плохих" исходных данных (например, при экспоненциальном возрастании элементов) время работы может ухудшиться до <tex> O(n) </tex>. | ||
| + | |||
| + | === Реализация === | ||
| + | Приведем код функции <tex> interpolation\_search(a, n, x) </tex> на языке C++. | ||
| + | <code> | ||
| + | int interpolation_search(double* a, int n, double x) | ||
| + | { | ||
| + | int l = 0; | ||
| + | int r = n - 1; | ||
| + | int m; | ||
| + | |||
| + | while (a[l] <= x && x <= a[r]) | ||
| + | { | ||
| + | mid = l + (x - a[l]) / (a[r] - a[l]) * (r - l); | ||
| + | |||
| + | if (a[m] == x) | ||
| + | return m; | ||
| + | if (a[m] < x) | ||
| + | l = m + 1; | ||
| + | else | ||
| + | r = m - 1; | ||
| + | } | ||
| + | |||
| + | if (a[l] == x) | ||
| + | return l; | ||
| + | else | ||
| + | return -1; // not found | ||
| + | } | ||
| + | </code> | ||
| + | |||
| + | === Полезные ссылки === | ||
| + | Д.Э. Кнут: [http://books.google.com/books?id=92rW-nktlbgC&pg=PA452&lpg=PA453&ots=jChsP2sutg&dq=%D0%BA%D0%BD%D1%83%D1%82+%D0%B8%D0%BD%D1%82%D0%B5%D1%80%D0%BF%D0%BE%D0%BB%D1%8F%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D1%8B%D0%B9+%D0%BF%D0%BE%D0%B8%D1%81%D0%BA&hl=ru&ie=windows-1251&output=html Искусство программирования (том 3)] <br/> | ||
| + | Wikipedia: [http://en.wikipedia.org/wiki/Interpolation_search Interpolation search] | ||
Версия 04:28, 12 июня 2011
Содержание
Идея
Рассмотрим задачу: найти слово в словаре. Если оно начинается на букву "А", то никто не будет искать его в середине, а откроет словарь ближе к началу. В чем разница между алгоритмом человека и другими? Отличие заключается в том, что алгоритмы вроде двоичного не делают различий между "немного больше" и "существенно больше".
Алгоритм
Пусть - отсортированный массив чисел из чисел, - значение, которое нужно найти. Если известно, что лежит между и , то следующая проверка выполняется примерно на расстоянии .
Время работы
При условии, что значения элементов близки к арифметической прогрессии, за один шаг алгоритм уменьшает количество проверяемых элементов с до . Поэтому среднее время работы алгоритма: . При "плохих" исходных данных (например, при экспоненциальном возрастании элементов) время работы может ухудшиться до .
Реализация
Приведем код функции на языке C++.
int interpolation_search(double* a, int n, double x)
{
int l = 0;
int r = n - 1;
int m;
while (a[l] <= x && x <= a[r])
{
mid = l + (x - a[l]) / (a[r] - a[l]) * (r - l);
if (a[m] == x)
return m;
if (a[m] < x)
l = m + 1;
else
r = m - 1;
}
if (a[l] == x)
return l;
else
return -1; // not found
}
Полезные ссылки
Д.Э. Кнут: Искусство программирования (том 3)
Wikipedia: Interpolation search