Встречное дерево Фенвика — различия между версиями
Proshev (обсуждение | вклад) |
Proshev (обсуждение | вклад) (→Любой отрезок в виде дизъюнктивных объединений отрезков, взятых из прямого и встречного дерева Фенвика) |
||
| Строка 6: | Строка 6: | ||
Вспомним, что <tex>h(i)</tex> возвращает количество единиц в двоичной записи числа <tex>i</tex>, а каждый столбец прямого дерева Фенвика вычисляется по формуле <tex>F(i) = \sum_{j=i-2^{h(i)}+1}^i a[j]</tex> | Вспомним, что <tex>h(i)</tex> возвращает количество единиц в двоичной записи числа <tex>i</tex>, а каждый столбец прямого дерева Фенвика вычисляется по формуле <tex>F(i) = \sum_{j=i-2^{h(i)}+1}^i a[j]</tex> | ||
| − | == Любой отрезок в виде дизъюнктивных объединений отрезков, | + | == Любой отрезок в виде дизъюнктивных объединений отрезков == |
| + | |||
| + | Представим встречное дерево Фенвика <tex>2^n</tex> на <tex>2^n</tex> и посмотрим на него, как на дерево отрезков. | ||
| + | |||
| + | В нем существует отрезок длины 1..<tex>2^n</tex>. Оставшуюся часть можно разбить на 2 поддерева. То есть получается структура обычного дерева отрезков, для которого известно указанное выше утверждение. | ||
== Свойства == | == Свойства == | ||
Версия 06:14, 15 июня 2011
| Определение: |
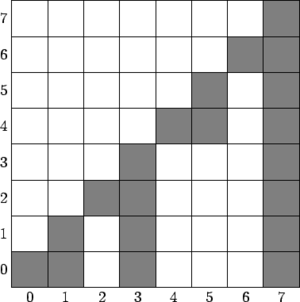
| Встречное дерево Фенвика — дерево Фенвика, в котором над каждым столбцом идет столбец такой же высоты, вычисляемый по формуле . |
Вспомним, что возвращает количество единиц в двоичной записи числа , а каждый столбец прямого дерева Фенвика вычисляется по формуле
Содержание
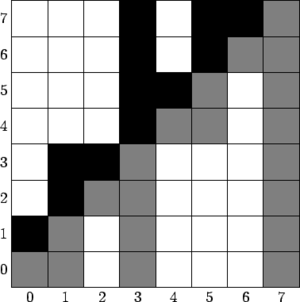
Любой отрезок в виде дизъюнктивных объединений отрезков
Представим встречное дерево Фенвика на и посмотрим на него, как на дерево отрезков.
В нем существует отрезок длины 1... Оставшуюся часть можно разбить на 2 поддерева. То есть получается структура обычного дерева отрезков, для которого известно указанное выше утверждение.
Свойства
Встречное дерево Фенвика - это структура данных, дерево на массиве, обладающее следующими свойствами:
1) позволяет вычислять значение некоторой операции на любом отрезке за время ;
2) позволяет изменять значение любого элемента за ;
3) требует памяти, а точнее, ровно столько же, сколько и массив из элементов;
4) легко обобщается на случай многомерных массивов.
5) позволяет представить любой отрезок в виде дизъюнктивных объединений отрезков, взятых из прямого и встречного дерева Фенвика.
Применение
Встречное дерево Фенвика применяется, когда нужно посчитать некоторую операцию на структуре без использования обратного элемента по этой операции. Например, перед нами стоит задача посчитать произведение матриц, не считая обратных. С помощью встречного дерева Фенвика можно разложить запрос произведения на отрезке на дизъюнктных отрезков, операция для которых уже посчитана, получается почти как в дереве отрезков.