Сеть Бетчера — различия между версиями
Gemin (обсуждение | вклад) (→Определение) |
|||
| Строка 1: | Строка 1: | ||
{{В разработке}} | {{В разработке}} | ||
==Определение== | ==Определение== | ||
| − | <b>Сеть Бетчера (Batcher odd-even mergesort)</b> - сортирующая сеть размером <tex>O(n log^2n)</tex> и глубиной <tex>O(log^2n)</tex>, где <tex>n</tex> - количество элементов для сортировки. | + | <b>Сеть Бетчера (Batcher odd-even mergesort)</b> - сортирующая сеть размером <tex>O(n \log^2n)</tex> и глубиной <tex>O(\log^2n)</tex>, где <tex>n</tex> - количество элементов для сортировки. |
| + | |||
==Конструирование сети== | ==Конструирование сети== | ||
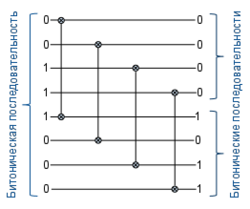
Для начала введем понятие битонической последовательности: | Для начала введем понятие битонической последовательности: | ||
Версия 06:24, 15 июня 2011
Эта статья находится в разработке!
Определение
Сеть Бетчера (Batcher odd-even mergesort) - сортирующая сеть размером и глубиной , где - количество элементов для сортировки.
Конструирование сети
Для начала введем понятие битонической последовательности:
| Определение: |
| Битонической последовательностью называется последовательность, которая сначала монотонно возрастает, а затем монотонно убывает, или последовательность, которая приводится к такому виду путем циклического сдвига. |
В нашем случае мы будем рассматривать нуль-единичные битонические последовательности:
| Определение: |
| Нуль-единичные битонические последовательности - последовательности вида или для |
На первом этапе конструирования стоит задача построить сравнивающую сеть, которая будет сортировать любую нуль-единичную битоническую последовательность - битонический сортировщик.
Битонический сортировщик состоит из нескольких каскадов, каждый из которых называется полуфильтром (half-cleaner). Каждый полуфильтр - сравнивающая сеть глубиной 1, в которой -й входной провод сравнивается со входным проводом с номером , где .
| Лемма: |
Если на вход в полуфильтр подать битоническую последовательность из нулей и единиц длиной , то на выходе мы получим две битонические последовательности длиной такие, что каждый элемент из верхней последовательности не превосходит любой элемент из нижней, и что одна из них будет однородной (clean) - состоящей либо из нулей, либо из единиц. |