Многомерное дерево отрезков — различия между версиями
VVolochay (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 56 промежуточных версий 9 участников) | |||
| Строка 1: | Строка 1: | ||
| − | [[Дерево отрезков. Построение|Дерево отрезков]] | + | [[Дерево отрезков. Построение|Дерево отрезков]] естественным образом обобщается на двумерный и, вообще говоря, многомерный случай. Такая структура данных может вычислять значение некоторой [[Ассоциативная_операция|ассоциативной функции]] на гиперпрямоугольнике. Например, она позволяет решать следующую задачу.{{Задача|definition = Дан <tex>p</tex>-мерный массив, где индекс каждого измерения массива может принимать значения от <tex>1</tex> до <tex>n</tex>. Необходимо уметь изменять значение элемента массива, а также находить сумму на <tex>p</tex>-мерной области. }} |
| − | {{Задача | + | Каждую из этих операций многомерное дерево отрезков выполняет за <tex>O(\log^{p} n)</tex>. |
| − | |definition= | ||
| − | |||
| − | } | ||
| − | == | + | К примерам задач, решаемых с помощью многомерного дерева отрезков, также можно отнести задачи, которые решаются с помощью одномерного [[Дерево отрезков. Построение|дерева отрезков]], только теперь в многомерном случае, а еще ,например, задачу поиска числа точек в заданном прямоугольнике, которую иначе можно решать при помощи [[Перечисление точек в произвольном прямоугольнике за n * log ^(d - 1) n (range tree)|range tree]], и другие. |
| − | Пусть задано <tex>p</tex>-мерное пространство с координатными осями <tex>x_1, x_2, x_3 | + | |
| + | ==Принцип работы== | ||
| + | [[Файл:SegmentTreeWorking.png|thumb|600px|right|Пример некоторой стадии работы алгоритма (поиск элементов, подходящих некоторой области)]] | ||
| + | <tex>n</tex>-мерное дерево отрезков {{---}} обычное дерево отрезков, элементами которого являются деревья отрезков размерности на единицу меньше. Основная идея заключается в рекурсивном переходе к деревьям меньшей размерности. Рассмотрим работу этого принципа на следующем примере. Пусть задано <tex>p</tex>-мерное пространство с координатными осями <tex>x_1, x_2, x_3 \ldots x_p</tex>. Необходимо найти значение некоторой ассоциативной функции на гиперпрямоугольнике. | ||
| + | |||
| + | Функция, вычисляющая ответ, должна работать следующим образом. На вход она принимает <tex>i</tex>-мерное дерево отрезков, которое соответствует рассматриваемой области (где <tex>i</tex> {{---}} количество координатных осей, которые не были рассмотрены), а также <tex>i</tex>-мерную область, для которой следует вычислить функцию. Вначале она находит <tex>i-1</tex>-мерные деревья отрезков, которые соответствуют отрезку по <tex>p-i+1</tex> координате, и рекурсивно запускается от них (если текущее дерево одномерное, то функция просто возвращает ответ из соответствующего листа). После этого считает итоговый результат, используя полученные после рекурсивных вызовов значения. | ||
| − | + | Для того, чтобы определить, от каких именно деревьев отрезков следует запускаться рекурсивно, действовать необходимо так же, как и в одномерном случае. Т. е. если текущий отрезок не пересекается с необходимым, то возвращаем нейтральный элемент, если он полностью лежит в необходимом отрезке, то рекурсивно переходим к следующей координате, иначе разобьем текущий отрезок пополам, и рассмотри отдельно каждую из частей. | |
| − | |||
| − | |||
| − | |||
| − | + | На рисунке справа показан пример обработки очередной координаты (поиск соответствующих отрезку элементов {{---}} деревьев на <tex>1</tex> меньшей мерности). | |
| − | + | Таким образом, алгоритм совершит <tex>p</tex> вхождений в рекурсию, каждая итерация которой работает за <tex>O(\log n)</tex> и получим необходимую асимптотику. | |
==Хранение== | ==Хранение== | ||
| − | [[Файл: | + | [[Файл:SegmentTree2DExample.png|thumb|350px|right|Пример двумерного дерева отрезков для 16 элементов]] |
| + | Пусть необходимо хранить дерево отрезков для <tex>p</tex>-мерной области, размеры которой <tex>n_1 \times n_2 \times \ldots \times n_p</tex>. Удобнее всего это делать с помощью <tex>p</tex>-мерного массива. Однако его размеры по каждой координате, так же как и в одномерном случае, должны превышать размеры соответствующего отрезка в 4 раза. На самом деле нам нужно хранить <tex>2n</tex> чисел, но, если мы хотим, чтобы правый и левый сын некоторой вершины <tex>i</tex> находились на <tex> 2i + 1</tex> и <tex>2i + 2</tex> месте, то, если длина отрезка не является степенью двойки, некоторые элементы массива могут быть не задействованы, поэтому в худшем случае, может понадобиться массив, размер которого в 4 раза превышает количество элементов. Т. е. потребуется массив размером <tex>4 n_1 \times 4 n_2 \times \ldots \times 4 n_p</tex>. Так двумерное дерево отрезков удобно хранить в виде массива, размером <tex>4N \times 4M</tex>. Каждая строчка такого массива соответствует некоторому отрезку по первой координате. Сама же строчка является деревом отрезков по второй координате. | ||
| + | |||
| + | На рисунке справа показан пример дерева отрезков для суммы на массиве 4 на 4, заполненного числами от 1 от 16. Например, в элементе <tex>a[2][0] = 100</tex> хранится сумма элементов, соответствующих отрезку <tex>[2..3]</tex> по первой координате и <tex>[0..3]</tex> по второй в исходном массиве. А в ячейке <tex>a[0][0] = 136</tex> хранится сумма всех элементов. | ||
| + | |||
| + | Интересно, что если построить дерево вначале по второй координате, а потом по первой, то получившийся массив будет таким же. Т. е. данный двумерный массив можно рассматривать как массив деревьев отрезков, где каждое дерево соответствует некоторому отрезку по второй координате, а в нем хранятся суммы по первой. | ||
| + | |||
| + | Заметим, что в общем случае для хранения <tex>p</tex>-мерного дерева отрезков требуется <tex>4^p n</tex> памяти, где <tex>n</tex> {{---}} общее количество элементов. | ||
| − | == | + | ==Запрос== |
| − | + | Рассмотрим отличия реализации многомерного и одномерного случаев. На самом деле, отличаются реализации только в двух местах. Во-первых, если рассматриваемый отрезок совпадает с необходимым, то в одномерном случае функция просто возвращает число, которое находится в текущем элементе массива. В многомерном случае, если рассматриваемая координата не последняя, следует вместо этого узнать значение, рекурсивно перейдя к следующей координате, и вернуть его. | |
| − | |||
| − | + | Еще один момент, в которых отличается реализация {{---}} передаваемые в функцию параметры. В многомерном случае кроме всего прочего следует также передать рассматриваемое <tex>p-i+1</tex>-мерное дерево (или кортеж из чисел, указывающих на соответствующие элементы массива), а также область, которую следует рассматривать (или <tex>p-i+1</tex> пар чисел, обозначающих отрезки на соответствующих координатных осях). Все остальные детали реализации остаются такими же как и в одномерном дереве отрезков. | |
| − | == | + | В каждом нижеприведенном псевдокоде будут встречены обозначения: |
| − | + | * индекс <tex>\mathtt{P}</tex> {{---}} размерность массива из условия задачи, | |
| − | * | + | * <tex>\mathtt{\odot}</tex> {{---}} та операция, которую мы считаем на данном многомерном дереве отрезков. |
| + | |||
| + | В нижеприведенном псевдокоде будет встречен <tex>\varepsilon</tex> {{---}} нейтральный элемент. | ||
| + | |||
| + | |||
| + | Псевдокод: | ||
| + | <code> | ||
| + | '''void''' query('''int''' area[], '''int''' x1, '''int''' x2, ..., '''int''' xP, '''int''' leftBorder, '''int''' rightBorder, '''int''' queryLeft, '''int''' queryRight, '''int''' node) | ||
| + | '''if''' queryLeft > queryRight | ||
| + | '''return''' <tex>\varepsilon</tex> | ||
| + | '''if''' leftBorder == queryLeft '''and''' rightBorder == queryRight | ||
| + | '''if''' последняя координата | ||
| + | '''return''' t[x1][x2]...[xP][node] | ||
| + | '''else''' | ||
| + | '''return''' query(area[], x1, x2, ..., xP, node, 0, m - 1, area[P + 2].left, area[P + 2].right, 0) | ||
| + | med = (leftBorder + rightBorder) / 2 | ||
| + | '''return''' query(area[], x1, x2, ..., xP, leftBorder, med, queryLeft, min(queryRight, med), node * 2 + 1) <tex>\odot</tex> | ||
| + | query(area[], x1, x2, ..., xP, med + 1, rightBorder, max(queryLeft, med + 1), queryRight, node * 2 + 2) | ||
| + | </code> | ||
| + | |||
| + | ==Обновление== | ||
| + | Как и в одномерном случае, обновить в массиве необходимо не один элемент, а все, которые отвечают за области, в которых он присутствует. Таким образом, при обработке отрезка по некоторой координате (если она не последняя) следует выполнить следующие действия: | ||
| + | * Если рассматриваемый отрезок содержит больше одного элемента, разобьем его на две части и рекурсивно перейдем в ту, где находится необходимый элемент | ||
| + | * Перейдем к следующей координате | ||
| + | Заметим, что "переходов к следующей координаты" при рассмотрении некоторой координатной оси будет совершено <tex>\log n</tex>, а итоговая сложность составит <tex>O(\log^{p} n)</tex>. | ||
| + | |||
| + | Отдельно следует рассмотреть, что происходит, когда текущее дерево является одномерным (мы рассмотрели все координаты, кроме текущей): | ||
| + | * Если рассматриваемый отрезок содержит больше одного элемента, разобьем его на две части и рекурсивно перейдем в ту, где находится необходимый элемент | ||
| + | * Найдем первую координату, в которой рассматривается больше одного элемента. Обновим значение элемента массива с помощью уже вычисленных значений для разбитого надвое отрезка по этой координате. | ||
| + | * Если мы рассматриваем область, состоящую из одного элемента, обновим значение массива. | ||
| + | |||
| + | Псевдокод: | ||
| + | <code> | ||
| + | '''void''' update('''int''' newElem, '''int''' x1, '''int''' x2, ..., '''int''' xP, '''int''' x1Left, '''int''' x1Right, '''int''' x2Left, '''int''' x2Right, ..., '''int''' xPLeft, '''int''' xPRight, | ||
| + | '''int''' leftBorder, '''int''' rightBorder, '''int''' node) | ||
| + | '''if''' leftBorder != rightBorder | ||
| + | med = (leftBorder + rightBorder) / 2 | ||
| + | '''if''' med >= newElem.x(P+1) | ||
| + | update(newElem, x1, x2, ..., xP, x1Left, x1Right, x2Left, x2Right, ..., xPLeft, xPRight, leftBorder, med, node * 2 + 1) | ||
| + | '''else''' | ||
| + | update(newElem, x1, x2, ..., xP, x1Left, x1Right, x2Left, x2Right, ..., xPLeft, xPRight, med + 1, rightBorder, node * 2 + 2) | ||
| + | '''if''' последняя координата | ||
| + | '''for''' I = 1..n | ||
| + | '''if''' xILeft != xIRigth | ||
| + | t[x1][x2]...[xP][node] = t[x1][x2]...[xI * 2 + 1]...[node] <tex>\odot</tex> t[x1][x2]...[xI * 2 + 2]...[node] | ||
| + | '''return''' | ||
| + | t[x1][x2]...[xP][node] = newElem.value | ||
| + | '''else''' | ||
| + | '''if''' leftBorder != rightBorder | ||
| + | update(newElem, x1, x2, ..., xP, node, x1Left, x1Rigth, x2Left, x2Right, ..., leftBorder, rightBorder, 0, m - 1, 0) | ||
| + | </code> | ||
| + | |||
| + | ==Построение== | ||
| + | Построение многомерного дерева отрезков практически ничем не отличается от его обновления. Единственное различие {{---}} если рассматриваемый отрезок состоит из более чем одного элемента, то необходимо рекурсивно вызываться из обеих частей. | ||
| + | |||
| + | Псевдокод: | ||
| + | <code> | ||
| + | '''void''' build('''int''' x1, '''int''' x2, ..., '''int''' xP, '''int''' x1Left, '''int''' x1Right, '''int''' x2Left, '''int''' x2Right, ..., '''int''' xPLeft, '''int''' xPRight, '''int''' leftBorder, | ||
| + | '''int''' rightBorder, '''int''' node) | ||
| + | '''if''' leftBorder != rightBorder | ||
| + | med = (leftBorder + rightBorder) / 2 | ||
| + | update(newElem, x1, x2, ..., xP, x1Left, x1Right, x2Left, x2Right, ..., xPLeft, xPRight, leftBorder, med, node * 2 + 1) | ||
| + | update(newElem, x1, x2, ..., xP, x1Left, x1Right, x2Left, x2Right, ..., xPLeft, xPRight, med + 1, rightBorder, node * 2 + 2) | ||
| + | '''if''' последняя координата | ||
| + | '''for''' I = 1..n | ||
| + | '''if''' xILeft != xIRight | ||
| + | t[x1][x2]...[xP][node] = t[x1][x2]...[xI * 2 + 1]...[node] <tex>\odot</tex> t[x1][x2]...[xI * 2 + 2]...[node] | ||
| + | '''return''' | ||
| + | t[x1][x2]...[xP][node] = data[x1Left][x2Left]...[xPLeft][node] | ||
| + | '''else''' | ||
| + | '''if''' leftBorder != rightBorder | ||
| + | update(newElem, x1, x2, ..., xP, node, x1Left, x1Rigth, x2Left, x2Right, ..., leftBorder, rightBorder, 0, m - 1, 0) | ||
| + | </code> | ||
| + | |||
| + | Заметим, что построение дерева требует <tex>O(n)</tex> времени, где <tex>n</tex> {{---}} общее число элементов в массиве. | ||
==См. также== | ==См. также== | ||
| − | *[[Дерево отрезков. Построение]] | + | *[[Дерево отрезков. Построение]] |
| − | *[[Сжатое многомерное дерево отрезков]] | + | *[[Сжатое многомерное дерево отрезков]] |
| − | *[[Многомерное дерево Фенвика]] | + | *[[Многомерное дерево Фенвика]] |
| + | |||
| + | ==Источники информации== | ||
| + | * [http://e-maxx.ru/algo/segment_tree MAXimal :: algo :: Дерево отрезков] | ||
| + | * [http://habrahabr.ru/post/131072/)/ Habrahabr {{---}} Двумерное дерево отрезков] | ||
| + | |||
| + | |||
| + | [[Категория: Дискретная математика и алгоритмы]] | ||
| + | [[Категория: Дерево отрезков]] | ||
| + | [[Категория: Модификации структур данных]] | ||
Текущая версия на 19:39, 4 сентября 2022
Дерево отрезков естественным образом обобщается на двумерный и, вообще говоря, многомерный случай. Такая структура данных может вычислять значение некоторой ассоциативной функции на гиперпрямоугольнике. Например, она позволяет решать следующую задачу.
| Задача: |
| Дан -мерный массив, где индекс каждого измерения массива может принимать значения от до . Необходимо уметь изменять значение элемента массива, а также находить сумму на -мерной области. |
Каждую из этих операций многомерное дерево отрезков выполняет за .
К примерам задач, решаемых с помощью многомерного дерева отрезков, также можно отнести задачи, которые решаются с помощью одномерного дерева отрезков, только теперь в многомерном случае, а еще ,например, задачу поиска числа точек в заданном прямоугольнике, которую иначе можно решать при помощи range tree, и другие.
Содержание
Принцип работы
-мерное дерево отрезков — обычное дерево отрезков, элементами которого являются деревья отрезков размерности на единицу меньше. Основная идея заключается в рекурсивном переходе к деревьям меньшей размерности. Рассмотрим работу этого принципа на следующем примере. Пусть задано -мерное пространство с координатными осями . Необходимо найти значение некоторой ассоциативной функции на гиперпрямоугольнике.
Функция, вычисляющая ответ, должна работать следующим образом. На вход она принимает -мерное дерево отрезков, которое соответствует рассматриваемой области (где — количество координатных осей, которые не были рассмотрены), а также -мерную область, для которой следует вычислить функцию. Вначале она находит -мерные деревья отрезков, которые соответствуют отрезку по координате, и рекурсивно запускается от них (если текущее дерево одномерное, то функция просто возвращает ответ из соответствующего листа). После этого считает итоговый результат, используя полученные после рекурсивных вызовов значения.
Для того, чтобы определить, от каких именно деревьев отрезков следует запускаться рекурсивно, действовать необходимо так же, как и в одномерном случае. Т. е. если текущий отрезок не пересекается с необходимым, то возвращаем нейтральный элемент, если он полностью лежит в необходимом отрезке, то рекурсивно переходим к следующей координате, иначе разобьем текущий отрезок пополам, и рассмотри отдельно каждую из частей.
На рисунке справа показан пример обработки очередной координаты (поиск соответствующих отрезку элементов — деревьев на меньшей мерности).
Таким образом, алгоритм совершит вхождений в рекурсию, каждая итерация которой работает за и получим необходимую асимптотику.
Хранение
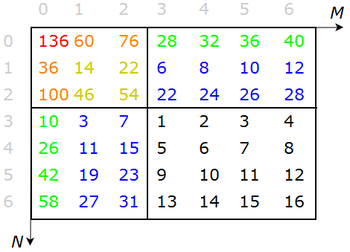
Пусть необходимо хранить дерево отрезков для -мерной области, размеры которой . Удобнее всего это делать с помощью -мерного массива. Однако его размеры по каждой координате, так же как и в одномерном случае, должны превышать размеры соответствующего отрезка в 4 раза. На самом деле нам нужно хранить чисел, но, если мы хотим, чтобы правый и левый сын некоторой вершины находились на и месте, то, если длина отрезка не является степенью двойки, некоторые элементы массива могут быть не задействованы, поэтому в худшем случае, может понадобиться массив, размер которого в 4 раза превышает количество элементов. Т. е. потребуется массив размером . Так двумерное дерево отрезков удобно хранить в виде массива, размером . Каждая строчка такого массива соответствует некоторому отрезку по первой координате. Сама же строчка является деревом отрезков по второй координате.
На рисунке справа показан пример дерева отрезков для суммы на массиве 4 на 4, заполненного числами от 1 от 16. Например, в элементе хранится сумма элементов, соответствующих отрезку по первой координате и по второй в исходном массиве. А в ячейке хранится сумма всех элементов.
Интересно, что если построить дерево вначале по второй координате, а потом по первой, то получившийся массив будет таким же. Т. е. данный двумерный массив можно рассматривать как массив деревьев отрезков, где каждое дерево соответствует некоторому отрезку по второй координате, а в нем хранятся суммы по первой.
Заметим, что в общем случае для хранения -мерного дерева отрезков требуется памяти, где — общее количество элементов.
Запрос
Рассмотрим отличия реализации многомерного и одномерного случаев. На самом деле, отличаются реализации только в двух местах. Во-первых, если рассматриваемый отрезок совпадает с необходимым, то в одномерном случае функция просто возвращает число, которое находится в текущем элементе массива. В многомерном случае, если рассматриваемая координата не последняя, следует вместо этого узнать значение, рекурсивно перейдя к следующей координате, и вернуть его.
Еще один момент, в которых отличается реализация — передаваемые в функцию параметры. В многомерном случае кроме всего прочего следует также передать рассматриваемое -мерное дерево (или кортеж из чисел, указывающих на соответствующие элементы массива), а также область, которую следует рассматривать (или пар чисел, обозначающих отрезки на соответствующих координатных осях). Все остальные детали реализации остаются такими же как и в одномерном дереве отрезков.
В каждом нижеприведенном псевдокоде будут встречены обозначения:
- индекс — размерность массива из условия задачи,
- — та операция, которую мы считаем на данном многомерном дереве отрезков.
В нижеприведенном псевдокоде будет встречен — нейтральный элемент.
Псевдокод:
void query(int area[], int x1, int x2, ..., int xP, int leftBorder, int rightBorder, int queryLeft, int queryRight, int node)
if queryLeft > queryRight
return
if leftBorder == queryLeft and rightBorder == queryRight
if последняя координата
return t[x1][x2]...[xP][node]
else
return query(area[], x1, x2, ..., xP, node, 0, m - 1, area[P + 2].left, area[P + 2].right, 0)
med = (leftBorder + rightBorder) / 2
return query(area[], x1, x2, ..., xP, leftBorder, med, queryLeft, min(queryRight, med), node * 2 + 1)
query(area[], x1, x2, ..., xP, med + 1, rightBorder, max(queryLeft, med + 1), queryRight, node * 2 + 2)
Обновление
Как и в одномерном случае, обновить в массиве необходимо не один элемент, а все, которые отвечают за области, в которых он присутствует. Таким образом, при обработке отрезка по некоторой координате (если она не последняя) следует выполнить следующие действия:
- Если рассматриваемый отрезок содержит больше одного элемента, разобьем его на две части и рекурсивно перейдем в ту, где находится необходимый элемент
- Перейдем к следующей координате
Заметим, что "переходов к следующей координаты" при рассмотрении некоторой координатной оси будет совершено , а итоговая сложность составит .
Отдельно следует рассмотреть, что происходит, когда текущее дерево является одномерным (мы рассмотрели все координаты, кроме текущей):
- Если рассматриваемый отрезок содержит больше одного элемента, разобьем его на две части и рекурсивно перейдем в ту, где находится необходимый элемент
- Найдем первую координату, в которой рассматривается больше одного элемента. Обновим значение элемента массива с помощью уже вычисленных значений для разбитого надвое отрезка по этой координате.
- Если мы рассматриваем область, состоящую из одного элемента, обновим значение массива.
Псевдокод:
void update(int newElem, int x1, int x2, ..., int xP, int x1Left, int x1Right, int x2Left, int x2Right, ..., int xPLeft, int xPRight,
int leftBorder, int rightBorder, int node)
if leftBorder != rightBorder
med = (leftBorder + rightBorder) / 2
if med >= newElem.x(P+1)
update(newElem, x1, x2, ..., xP, x1Left, x1Right, x2Left, x2Right, ..., xPLeft, xPRight, leftBorder, med, node * 2 + 1)
else
update(newElem, x1, x2, ..., xP, x1Left, x1Right, x2Left, x2Right, ..., xPLeft, xPRight, med + 1, rightBorder, node * 2 + 2)
if последняя координата
for I = 1..n
if xILeft != xIRigth
t[x1][x2]...[xP][node] = t[x1][x2]...[xI * 2 + 1]...[node] t[x1][x2]...[xI * 2 + 2]...[node]
return
t[x1][x2]...[xP][node] = newElem.value
else
if leftBorder != rightBorder
update(newElem, x1, x2, ..., xP, node, x1Left, x1Rigth, x2Left, x2Right, ..., leftBorder, rightBorder, 0, m - 1, 0)
Построение
Построение многомерного дерева отрезков практически ничем не отличается от его обновления. Единственное различие — если рассматриваемый отрезок состоит из более чем одного элемента, то необходимо рекурсивно вызываться из обеих частей.
Псевдокод:
void build(int x1, int x2, ..., int xP, int x1Left, int x1Right, int x2Left, int x2Right, ..., int xPLeft, int xPRight, int leftBorder,
int rightBorder, int node)
if leftBorder != rightBorder
med = (leftBorder + rightBorder) / 2
update(newElem, x1, x2, ..., xP, x1Left, x1Right, x2Left, x2Right, ..., xPLeft, xPRight, leftBorder, med, node * 2 + 1)
update(newElem, x1, x2, ..., xP, x1Left, x1Right, x2Left, x2Right, ..., xPLeft, xPRight, med + 1, rightBorder, node * 2 + 2)
if последняя координата
for I = 1..n
if xILeft != xIRight
t[x1][x2]...[xP][node] = t[x1][x2]...[xI * 2 + 1]...[node] t[x1][x2]...[xI * 2 + 2]...[node]
return
t[x1][x2]...[xP][node] = data[x1Left][x2Left]...[xPLeft][node]
else
if leftBorder != rightBorder
update(newElem, x1, x2, ..., xP, node, x1Left, x1Rigth, x2Left, x2Right, ..., leftBorder, rightBorder, 0, m - 1, 0)
Заметим, что построение дерева требует времени, где — общее число элементов в массиве.