Алгоритм Фарака-Колтона и Бендера — различия между версиями
(→Минимум внутри блока) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 37 промежуточных версий 12 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Алгоритм Фарака-Колтона, Бендера ( | + | '''Алгоритм Фарака-Колтона, Бендера''' (англ. ''Farach-Colton, Bender'') — применяется для решения за <tex>\langle O(N),O(1) \rangle</tex> времени специального случая задачи <tex>\mathrm{RMQ}</tex> (поиск минимума на отрезке), в котором соседние элементы входной последовательности различаются на <tex>\pm 1</tex>. Может быть использован также для [[Сведение задачи LCA к задаче RMQ|решения задачи <tex>\mathrm{LCA}</tex>]]. |
| − | + | {{Задача | |
| − | + | |definition = Дан массив <tex>A[1 \ldots N]</tex> целых чисел, соседние элементы которого отличаются на <tex>\pm 1</tex>. Поступают онлайн запросы вида <tex>(l, r)</tex>, для каждого из которых требуется найти минимум среди элементов <tex>A[l], A[l + 1], \ldots, A[r] </tex>. | |
| + | }} | ||
== Алгоритм == | == Алгоритм == | ||
| − | |||
| − | Данный алгоритм основывается на методе решения задачи RMQ с помощью [[Решение RMQ с помощью разреженной таблицы|разреженной таблицы | + | Данный алгоритм основывается на методе решения задачи <tex>\mathrm{RMQ}</tex> с помощью [[Решение RMQ с помощью разреженной таблицы|разреженной таблицы]] за <tex>\langle O(N \log N),O(1) \rangle</tex>. |
| + | |||
| + | Чтобы избавиться от логарифма используется предподсчёт ответа для небольших подстрок входной последовательности. Разделим последовательность <tex>A_i</tex> на блоки длины <tex>K=\dfrac{1}{2}\log_2 N</tex>. Для каждого блока вычислим минимум на нём и определим <tex>B_i</tex> как позицию минимального элемента в <tex>i</tex>-ом блоке. | ||
| + | |||
| + | |||
| − | + | На новой последовательности <tex>B_i</tex> построим [[Решение RMQ с помощью разреженной таблицы|разреженную таблицу]]. При этом размер разреженной таблицы и время её построения будут равны: | |
| − | + | <tex>\dfrac{N}{K}\log\dfrac{N}{K}=\bigg(\dfrac{2N}{\log N}\bigg)\log\bigg(\dfrac{2N}{\log N}\bigg)=\bigg(\dfrac{2N}{\log N}\bigg)\bigg(1+\log\bigg(\dfrac{N}{\log N}\bigg)\bigg)\leqslant \dfrac{2N}{\log N}</tex> <tex>+2N=O(N)</tex> | |
| − | |||
| − | |||
| − | |||
| − | |||
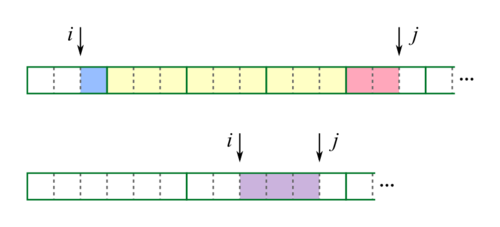
| − | Второй элемент мы уже умеем находить за <tex>O(1)</tex> с помощью <tex> | + | Теперь для ответа на запрос <tex>\mathrm{RMQ}</tex><tex>[l:r]</tex>, если <tex>l</tex> и <tex>r</tex> находятся в разных блоках, нам необходимо вычислить следующее: |
| + | * минимум на отрезке от <tex>l</tex> до конца блока, содержащего <tex>l</tex>; | ||
| + | * минимум по всем блокам, находящимся между блоками, содержащими <tex>l</tex> и <tex>r</tex>; | ||
| + | * минимум от начала блока, содержащего <tex>r</tex>, до <tex>r</tex>. | ||
| + | Ответом на запрос будет позиция меньшего из этих трёх элементов. | ||
| + | |||
| + | [[Файл:F-C_B_algo.png|500px|center|Части, из которых состоит ответ на запрос RMQ]] | ||
| + | |||
| + | Второй элемент мы уже умеем находить за <tex>O(1)</tex> с помощью <tex>B_i</tex> и разреженной таблицы. Осталось научиться находить минимум по отрезку, границы которого не совпадают с границами блоков. | ||
=== Минимум внутри блока === | === Минимум внутри блока === | ||
| Строка 23: | Строка 31: | ||
{{Утверждение | {{Утверждение | ||
|id=sameblocks | |id=sameblocks | ||
| − | |statement=Если две последовательности <tex>x_i</tex> и <tex>y_i</tex> таковы, что все их элементы на соответствующих позициях различаются на одну и ту же константу | + | |statement=Если две последовательности <tex>x_i</tex> и <tex>y_i</tex> таковы, что все их элементы на соответствующих позициях различаются на одну и ту же константу (т.е. <tex>\forall k: x_k = y_k + C</tex>), то любой запрос <tex>\mathrm{RMQ}</tex> даст один и тот же ответ для обеих последовательностей. |
}} | }} | ||
| Строка 31: | Строка 39: | ||
|id=kindscount | |id=kindscount | ||
|statement=Существует <tex>O(\sqrt N)</tex> различных типов нормализованных блоков. | |statement=Существует <tex>O(\sqrt N)</tex> различных типов нормализованных блоков. | ||
| − | |proof=Соседние элементы в блоках отличаются на | + | |proof=Соседние элементы в блоках отличаются на <tex>\pm 1</tex>. Первый элемент в нормализованном блоке всегда равен нулю. Таким образом, каждый нормализованный блок может быть представлен <tex>\pm 1</tex>-вектором длины <tex> \bigg(\dfrac{1}{2} \log_2 N\bigg) - 1</tex>. Таких векторов <tex>2^{(\frac{1}{2} \log_2 N) - 1} = O(\sqrt N)</tex>. |
}} | }} | ||
| − | Осталось создать <tex>O(\sqrt N)</tex> таблиц | + | Осталось создать <tex>O(\sqrt N)</tex> таблиц {{---}} по одной для каждого типа блока. В такую таблицу необходимо занести предподсчитанные ответы на все возможные запросы минимума внутри блока соответствующего типа, которых <tex>\bigg(\dfrac{1}{2}\log_2 N\bigg)^2 = O(\log^2 N)</tex>. Для каждого блока в <tex>B_i</tex> необходимо заранее вычислить его тип. Для этого нужно подобрать некоторую функцию из множества блоков в множество натуральных чисел, не вызывающую коллизий. Например, вектор из нулей и единиц, соответствующий типу блока, можно записать в целочисленный тип. Таким образом мы получили возможность отвечать на запрос минимума по любой части блока за <tex>O(1)</tex>, затратив на предподсчёт <tex>O(N)</tex> времени. |
| + | |||
| + | === Псевдокод === | ||
| + | |||
| + | '''function''' precalc(A: '''int[N]'''): | ||
| + | block_size = log(N) / 2 <font color=green> // размеры блоков </font> | ||
| + | K = <tex>\lceil</tex>N / block_size<tex>\rceil</tex> <font color=green> // количество блоков </font> | ||
| + | <font color=green>// предподсчитаем позиции минимумов в каждом блоке</font> | ||
| + | cur_block = -1 | ||
| + | '''for''' i = 0 '''to''' K - 1 | ||
| + | B[i] = -1 | ||
| + | '''for''' i = 0 '''to''' N - 1 | ||
| + | '''if''' i '''mod''' block_size == 0 | ||
| + | cur_block++ | ||
| + | '''if''' B[cur_block] = -1 '''or''' A[B[cur_block]] > A[i] | ||
| + | B[cur_block] = i | ||
| + | <font color=green>// построим Sparse table на массиве B</font> | ||
| + | '''for''' i = 0 '''to''' K - 1 | ||
| + | ST[i][0] = B[i] | ||
| + | '''for''' j = 1 '''to''' log(N) | ||
| + | '''for''' i = 0 '''to''' K - 1 | ||
| + | ind = (1 << (j - 1)) + i | ||
| + | '''if''' ind ≥ K | ||
| + | ST[i][j] = ST[i][j - 1] | ||
| + | '''else if''' A[ST[i][j - 1]] > A[ST[ind][j - 1]] | ||
| + | ST[i][j] = ST[ind][j - 1] | ||
| + | '''else''' | ||
| + | ST[i][j] = ST[i][j - 1] | ||
| + | <font color=green>// Посчитаем тип для каждого блока</font> | ||
| + | '''for''' i = 0 '''to''' K - 1 | ||
| + | type[i] = 0 | ||
| + | cur_block = 0 | ||
| + | j = 0 | ||
| + | i = 0 | ||
| + | '''while''' i < N or j < block_size | ||
| + | '''if''' j ≥ block_size | ||
| + | j = 0 | ||
| + | cur_block++ | ||
| + | '''if''' j > 0 '''and''' (i ≥ N '''or''' A[i - 1] < A[i]) | ||
| + | type[cur_block] += (1 << (j - 1)) | ||
| + | i++ | ||
| + | j++ | ||
| + | <font color=green>// Осталось только для каждого блока предподсчитать позиции минимумов на всех подотрезках</font> | ||
| + | '''for''' i = 0 '''to''' K - 1 | ||
| + | '''for''' l = 0 '''to''' block_size - 1 | ||
| + | '''for''' r = 0 '''to''' block_size - 1 | ||
| + | block_min[i][l][r] = -1 | ||
| + | '''for''' i = 0 '''to''' K - 1 | ||
| + | t = type[i] | ||
| + | '''if''' block_min[t][0][0] = -1 <font color=green>// если там записано, что-то отличное от -1, то значит, мы уже посчитали ответ для такого типа отрезков</font> | ||
| + | '''for''' l = 0 '''to''' block_size - 1 | ||
| + | block_min[t][l][l] = l | ||
| + | '''for''' r = l + 1 '''to''' block_size - 1 | ||
| + | block_min[t][l][r] = block_min[t][l][r - 1] | ||
| + | '''if''' i * block_size + r ≤ N '''and''' A[i * block_size + block_min[t][l][r]] > A[i * block_size + r] | ||
| + | block_min[t][l][r] = r | ||
| + | |||
| + | '''function''' block_RMQ(block_number: '''int''', l: '''int''', r: '''int'''): '''int''' | ||
| + | '''return''' block_min[type[block_number]][l][r] + block_number * block_size | ||
| + | |||
| + | '''function''' RMQ(l: '''int''', r: '''int'''): '''int''' | ||
| + | bl = l / block_size | ||
| + | br = r / block_size | ||
| + | '''if''' bl = br <font color=green>// если оба индекса внутри одного блока</font> | ||
| + | '''return''' A[block_RMQ(bl, l % block_size, r % block_size)] | ||
| + | '''if''' bl + 1 < br <font color=green>// найдем минимум на блоках между крайними, если таковые есть</font> | ||
| + | power = log(br - bl - 1) | ||
| + | ansb = min(A[ST[bl + 1][power]], A[ST[br - (1 << power)][power]]) | ||
| + | ansl = A[block_RMQ(bl, l % block_size, block_size - 1)] <font color=green>// найдем минимум на отрезке от l до конца блока, содержащего l</font> | ||
| + | ansr = A[block_RMQ(br, 0, r % block_size)] <font color=green>// найдем минимум от начала блока, содержащего r, до r </font> | ||
| + | '''return''' min(ansb, min(ansl, ansr)) | ||
=== Результат === | === Результат === | ||
| Строка 44: | Строка 122: | ||
* [[Сведение задачи LCA к задаче RMQ]] | * [[Сведение задачи LCA к задаче RMQ]] | ||
| − | == | + | ==Источники информации== |
| − | * M. A. | + | * Bender, M.A., Farach-Colton, M. {{---}} The LCA Problem Revisited. LATIN (2000), с. 88-94 |
| + | |||
| + | [[Категория: Алгоритмы и структуры данных]] | ||
| + | [[Категория: Задача о наименьшем общем предке]] | ||
Текущая версия на 19:39, 4 сентября 2022
Алгоритм Фарака-Колтона, Бендера (англ. Farach-Colton, Bender) — применяется для решения за времени специального случая задачи (поиск минимума на отрезке), в котором соседние элементы входной последовательности различаются на . Может быть использован также для решения задачи .
| Задача: |
| Дан массив целых чисел, соседние элементы которого отличаются на . Поступают онлайн запросы вида , для каждого из которых требуется найти минимум среди элементов . |
Содержание
Алгоритм
Данный алгоритм основывается на методе решения задачи с помощью разреженной таблицы за .
Чтобы избавиться от логарифма используется предподсчёт ответа для небольших подстрок входной последовательности. Разделим последовательность на блоки длины . Для каждого блока вычислим минимум на нём и определим как позицию минимального элемента в -ом блоке.
На новой последовательности построим разреженную таблицу. При этом размер разреженной таблицы и время её построения будут равны:
Теперь для ответа на запрос , если и находятся в разных блоках, нам необходимо вычислить следующее:
- минимум на отрезке от до конца блока, содержащего ;
- минимум по всем блокам, находящимся между блоками, содержащими и ;
- минимум от начала блока, содержащего , до .
Ответом на запрос будет позиция меньшего из этих трёх элементов.
Второй элемент мы уже умеем находить за с помощью и разреженной таблицы. Осталось научиться находить минимум по отрезку, границы которого не совпадают с границами блоков.
Минимум внутри блока
| Утверждение: |
Если две последовательности и таковы, что все их элементы на соответствующих позициях различаются на одну и ту же константу (т.е. ), то любой запрос даст один и тот же ответ для обеих последовательностей. |
Таким образом, мы можем нормализовать блок, вычтя из всех его элементов первый. Тем самым мы значительно уменьшим число возможных типов блоков.
| Утверждение: |
Существует различных типов нормализованных блоков. |
| Соседние элементы в блоках отличаются на . Первый элемент в нормализованном блоке всегда равен нулю. Таким образом, каждый нормализованный блок может быть представлен -вектором длины . Таких векторов . |
Осталось создать таблиц — по одной для каждого типа блока. В такую таблицу необходимо занести предподсчитанные ответы на все возможные запросы минимума внутри блока соответствующего типа, которых . Для каждого блока в необходимо заранее вычислить его тип. Для этого нужно подобрать некоторую функцию из множества блоков в множество натуральных чисел, не вызывающую коллизий. Например, вектор из нулей и единиц, соответствующий типу блока, можно записать в целочисленный тип. Таким образом мы получили возможность отвечать на запрос минимума по любой части блока за , затратив на предподсчёт времени.
Псевдокод
function precalc(A: int[N]): block_size = log(N) / 2 // размеры блоков K = N / block_size // количество блоков // предподсчитаем позиции минимумов в каждом блоке cur_block = -1 for i = 0 to K - 1 B[i] = -1 for i = 0 to N - 1 if i mod block_size == 0 cur_block++ if B[cur_block] = -1 or A[B[cur_block]] > A[i] B[cur_block] = i // построим Sparse table на массиве B for i = 0 to K - 1 ST[i][0] = B[i] for j = 1 to log(N) for i = 0 to K - 1 ind = (1 << (j - 1)) + i if ind ≥ K ST[i][j] = ST[i][j - 1] else if A[ST[i][j - 1]] > A[ST[ind][j - 1]] ST[i][j] = ST[ind][j - 1] else ST[i][j] = ST[i][j - 1] // Посчитаем тип для каждого блока for i = 0 to K - 1 type[i] = 0 cur_block = 0 j = 0 i = 0 while i < N or j < block_size if j ≥ block_size j = 0 cur_block++ if j > 0 and (i ≥ N or A[i - 1] < A[i]) type[cur_block] += (1 << (j - 1)) i++ j++ // Осталось только для каждого блока предподсчитать позиции минимумов на всех подотрезках for i = 0 to K - 1 for l = 0 to block_size - 1 for r = 0 to block_size - 1 block_min[i][l][r] = -1 for i = 0 to K - 1 t = type[i] if block_min[t][0][0] = -1 // если там записано, что-то отличное от -1, то значит, мы уже посчитали ответ для такого типа отрезков for l = 0 to block_size - 1 block_min[t][l][l] = l for r = l + 1 to block_size - 1 block_min[t][l][r] = block_min[t][l][r - 1] if i * block_size + r ≤ N and A[i * block_size + block_min[t][l][r]] > A[i * block_size + r] block_min[t][l][r] = r
function block_RMQ(block_number: int, l: int, r: int): int return block_min[type[block_number]][l][r] + block_number * block_size
function RMQ(l: int, r: int): int
bl = l / block_size
br = r / block_size
if bl = br // если оба индекса внутри одного блока
return A[block_RMQ(bl, l % block_size, r % block_size)]
if bl + 1 < br // найдем минимум на блоках между крайними, если таковые есть
power = log(br - bl - 1)
ansb = min(A[ST[bl + 1][power]], A[ST[br - (1 << power)][power]])
ansl = A[block_RMQ(bl, l % block_size, block_size - 1)] // найдем минимум на отрезке от l до конца блока, содержащего l
ansr = A[block_RMQ(br, 0, r % block_size)] // найдем минимум от начала блока, содержащего r, до r
return min(ansb, min(ansl, ansr))
Результат
Итого, на предподсчёт требуется времени и памяти, а ответ на запрос вычисляется за .
См. также
- Решение RMQ с помощью разреженной таблицы
- Сведение задачи RMQ к задаче LCA
- Сведение задачи LCA к задаче RMQ
Источники информации
- Bender, M.A., Farach-Colton, M. — The LCA Problem Revisited. LATIN (2000), с. 88-94