Лексикографический порядок — различия между версиями
(→Сравнение слов) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 55 промежуточных версий 8 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | {{Определение | |
| − | Пусть | + | |definition=Пусть даны две последовательности <tex> ~A = a_1 a_2 \dots a_n </tex> и <tex> ~B = b_1 b_2 \dots b_m </tex> |
| + | Тогда последовательность <tex> ~A </tex> '''лексикографически меньше''' (англ. ''lexicographically less'') последовательности <tex> ~B </tex>, если выполняется одно из двух условий: | ||
| + | *<tex> n < m </tex> и при этом <tex> a_i = b_i </tex> для всех <tex>i \in [1 .. n] </tex>, | ||
| + | * <tex> \exists k\leqslant \min(n, m): a_k < b_k </tex> и при этом <tex> \forall j : j < k ~a_j = b_j </tex>. | ||
| + | }} | ||
| − | == | + | Приведем псевдокод сравнения последовательностей из элементов множества '''Т''': |
| − | + | '''function''' compare(A, B : '''list <T>'''): '''Ord''' <font color=green>// Возвращает "LT", если A < B, "GT", если A > B, или "EQ", если последовательности равны</font> | |
| + | '''for''' i = 1 '''to''' min(len(A), len(B)) | ||
| + | '''if''' A[i] < B[i] <font color=green> // i-й элемент А меньше i-го элемента B, но префиксы длины i - 1 равны</font> | ||
| + | '''return''' LT | ||
| + | '''if''' A[i] > B[i] <font color=green> // i-й элемент А больше i-го элемента B, но префиксы длины i - 1 равны</font> | ||
| + | '''return''' GT | ||
| + | '''if''' len(A) < len(B) <font color=green>// А {{---}} префикс В, но не равна ей</font> | ||
| + | '''return''' LT | ||
| + | '''if''' len(A) > len(B) <font color=green>// В {{---}} префикс А, но не равна ей</font> | ||
| + | '''return''' GT | ||
| + | '''return''' EQ <font color=green>// Длины последовательностей и все элементы равны</font> | ||
| + | {{Определение | ||
| + | |definition=Последовательности записаны в '''лексикографическом порядке''' (англ. ''lexicographical order''), если для любых <tex> i<j </tex> выполняется неравенство <tex> S_i<S_j </tex>, где <tex> S_i </tex> и <tex> S_j </tex> последовательности с номерами <tex> i </tex> и <tex> j </tex>. | ||
| + | }} | ||
| + | Например, слово "сон" лексикографически меньше слова "сонный", так как оно является его префиксом. Слово "низ" лексикографически меньше слова "нос", поскольку первые символы совпадают, а второй символ первого слова меньше, чем второй символ второго. | ||
| − | |||
| − | |||
| − | |||
| − | + | == Примеры == | |
| − | + | * Перестановки (<font color=#c355a0>'''светло-фиолетовым выделен'''</font> общий префикс, <font color=#992574>'''темно-фиолетовым'''</font> первый отличный элемент, так как <tex>4 < 6</tex>, то первая перестановка лексикографически меньше) | |
| − | + | {| cellpadding="4" style="margin-left: left; margin-right: left;" | |
| − | + | | [[Файл:Compareperm.png]] | |
| − | + | |} | |
| − | + | * Сочетания (так как <tex>4 < 6</tex>, то первое сочетание лексикографически меньше) | |
| − | + | {| cellpadding="4" style="margin-left: left; margin-right: left;" | |
| − | + | | [[Файл:Comparechoose.png]] | |
| − | + | |} | |
| − | + | * [[комбинаторные объекты|Разбиение на слагаемые]] (так как <tex>4 < 9</tex>, то первое разбиение на слагаемые лексикографически меньше) | |
| − | + | {| cellpadding="4" style="margin-left: left; margin-right: left;" | |
| − | + | | [[Файл:Compare part.png]] | |
| − | + | |} | |
| − | + | * Последовательность чисел в любой системе счисления, записанных в фиксированной разрядной сетке (<tex>000</tex>, <tex>001</tex>, <tex>002</tex>, <tex>003</tex>, <tex>004</tex>, <tex>005</tex>, <tex>\dots</tex>, <tex>999</tex>). | |
| − | + | * Порядок слов в словаре. Предполагается, что буквы можно сравнивать, сравнивая их номера в алфавите. Тогда лексикографический порядок {{---}} это, например, <tex>AAA</tex>, <tex>AAB</tex>, <tex>AAC</tex>, <tex>AAD</tex>, <tex>\dots</tex>, <tex>ZZZ</tex>. | |
| + | * Эти слова тоже записаны в лексикографическом порядке: <tex>airport</tex>, <tex>duck</tex>, <tex>horse</tex>, <tex>house</tex>, <tex>sleep</tex>. | ||
| − | + | == См. также == | |
| + | * [[Генерация комбинаторных объектов в лексикографическом порядке]] | ||
| + | * [[Получение предыдущего объекта]] | ||
| + | * [[Получение следующего объекта]] | ||
| + | == Источники информации== | ||
| + | *[http://en.wikipedia.org/wiki/Lexicographical_order Wikipedia {{---}} Lexicographical order] | ||
| + | *[http://ru.wikipedia.org/wiki/%D0%9B%D0%B5%D0%BA%D1%81%D0%B8%D0%BA%D0%BE%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%BF%D0%BE%D1%80%D1%8F%D0%B4%D0%BE%D0%BA Википедия {{---}} Лексикографический порядок ] | ||
| − | + | [[Категория: Дискретная математика и алгоритмы]] | |
| − | + | [[Категория: Комбинаторика ]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Текущая версия на 19:03, 4 сентября 2022
| Определение: |
| Пусть даны две последовательности и
Тогда последовательность лексикографически меньше (англ. lexicographically less) последовательности , если выполняется одно из двух условий:
|
Приведем псевдокод сравнения последовательностей из элементов множества Т:
function compare(A, B : list <T>): Ord // Возвращает "LT", если A < B, "GT", если A > B, или "EQ", если последовательности равны
for i = 1 to min(len(A), len(B))
if A[i] < B[i] // i-й элемент А меньше i-го элемента B, но префиксы длины i - 1 равны
return LT
if A[i] > B[i] // i-й элемент А больше i-го элемента B, но префиксы длины i - 1 равны
return GT
if len(A) < len(B) // А — префикс В, но не равна ей
return LT
if len(A) > len(B) // В — префикс А, но не равна ей
return GT
return EQ // Длины последовательностей и все элементы равны
| Определение: |
| Последовательности записаны в лексикографическом порядке (англ. lexicographical order), если для любых выполняется неравенство , где и последовательности с номерами и . |
Например, слово "сон" лексикографически меньше слова "сонный", так как оно является его префиксом. Слово "низ" лексикографически меньше слова "нос", поскольку первые символы совпадают, а второй символ первого слова меньше, чем второй символ второго.
Примеры
- Перестановки (светло-фиолетовым выделен общий префикс, темно-фиолетовым первый отличный элемент, так как , то первая перестановка лексикографически меньше)
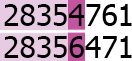
|
- Сочетания (так как , то первое сочетание лексикографически меньше)
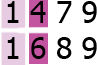
|
- Разбиение на слагаемые (так как , то первое разбиение на слагаемые лексикографически меньше)
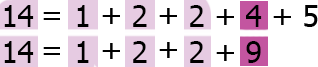
|
- Последовательность чисел в любой системе счисления, записанных в фиксированной разрядной сетке (, , , , , , , ).
- Порядок слов в словаре. Предполагается, что буквы можно сравнивать, сравнивая их номера в алфавите. Тогда лексикографический порядок — это, например, , , , , , .
- Эти слова тоже записаны в лексикографическом порядке: , , , , .