Эквивалентность состояний ДКА — различия между версиями
Leugenea (обсуждение | вклад) м (Пунктуация и орфография) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 72 промежуточные версии 16 участников) | |||
| Строка 1: | Строка 1: | ||
| + | == Связь эквивалентности состояний и различимости состояний == | ||
| + | |||
{{Определение | {{Определение | ||
| − | |definition = Два автомата <tex> \mathcal{A}_1 = \langle Q_1,\Sigma,\delta_1,s_{1}, T_1\subseteq Q_1 \rangle </tex> и <tex>\mathcal{A}_2 = \langle Q_2,\Sigma,\delta_2,s_{2}, T_2\subseteq Q_2 \rangle </tex> называются | + | |definition = Два автомата <tex> \mathcal{A}_1 = \langle Q_1,\Sigma,\delta_1,s_{1}, T_1\subseteq Q_1 \rangle </tex> и <tex>\mathcal{A}_2 = \langle Q_2,\Sigma,\delta_2,s_{2}, T_2\subseteq Q_2 \rangle </tex> называются '''эквивалентными''' (англ. ''equivalent''), если они распознают один и тот же язык над алфавитом <tex>\Sigma</tex>, то есть <tex>\mathcal{L}(\mathcal{A}_1) = \mathcal{L}(\mathcal{A}_2)</tex>. |
}} | }} | ||
{{Определение | {{Определение | ||
| − | |definition = Слово <tex>z \in \Sigma^*</tex> различает два состояния <tex>q_i</tex> и <tex>q_j</tex>, если | + | |definition = [[Основные определения, связанные со строками#string|Слово]] <tex>z \in \Sigma^*</tex> '''различает''' (англ. ''distinguish'') два состояния <tex>q_i</tex> и <tex>q_j</tex>, если |
| − | * <tex> \langle q_i, z \rangle \vdash^* \langle t_1, \varepsilon \rangle, \langle q_j, z \rangle \vdash^* \langle t_2, \varepsilon \rangle \Rightarrow t_1 \notin T \Leftrightarrow t_2 \in T </tex>. | + | * <tex> \langle q_i, z \rangle \vdash^* \langle t_1, \varepsilon \rangle, \langle q_j, z \rangle \vdash^* \langle t_2, \varepsilon \rangle \Rightarrow (t_1 \notin T \Leftrightarrow t_2 \in T) </tex>. |
}} | }} | ||
{{Определение | {{Определение | ||
| − | |definition = Два <em> состояния</em> <tex>q_i</tex> и <tex>q_j</tex> называются | + | |definition = Два <em> состояния</em> <tex>q_i</tex> и <tex>q_j</tex> называются '''эквивалентными''' <tex>(q_i \sim q_j)</tex>, если не существует [[Основные определения, связанные со строками#string|строки]], которая их различает, то есть <tex>\forall z \in \Sigma^*</tex> верно, что |
| − | * <tex> \langle q_i, z \rangle \vdash^* \langle t_1, \varepsilon \rangle, \langle q_j, z \rangle \vdash^* \langle t_2, \varepsilon \rangle \Rightarrow t_1 \in T \Leftrightarrow t_2 \in T </tex>. | + | * <tex> \langle q_i, z \rangle \vdash^* \langle t_1, \varepsilon \rangle, \langle q_j, z \rangle \vdash^* \langle t_2, \varepsilon \rangle \Rightarrow (t_1 \in T \Leftrightarrow t_2 \in T) </tex>. |
}} | }} | ||
| − | + | Заметим, что эквивалентность состояний действительно является [[Отношение эквивалентности|отношением эквивалентности]]. Так как <tex> \Leftrightarrow </tex> (равносильность) является отношением эквивалентности и в детерминированном автомате всегда существует путь по любому слову, описанное нами отношение является отношением эквивалентности. | |
| − | |||
| − | |||
| − | |||
{{Лемма | {{Лемма | ||
|statement = | |statement = | ||
| − | <tex> \mathcal{A} = \langle Q, \Sigma, \delta, s, T \rangle </tex> | + | <tex> \mathcal{A} = \langle Q, \Sigma, \delta, s, T \rangle </tex>, <tex> p_1, p_2, q_1, q_2 \in Q </tex>, <tex> q_i = \delta(p_i, c) </tex>, <tex> w \in \Sigma^*</tex> различает <tex> q_1 </tex> и <tex> q_2 </tex>. Тогда <tex>cw</tex> различает <tex> p_1 </tex> и <tex> p_2 </tex>. |
| − | |||
| − | |||
| − | |||
|proof = | |proof = | ||
<tex> \langle p_i, cw \rangle \vdash \langle q_i, w \rangle \vdash^* \langle t_i, \varepsilon \rangle </tex> | <tex> \langle p_i, cw \rangle \vdash \langle q_i, w \rangle \vdash^* \langle t_i, \varepsilon \rangle </tex> | ||
А значит, по условию различимости для <tex> q_1 </tex> и <tex> q_2</tex> , <tex> t_1 \in T \Leftrightarrow t_2 \notin T </tex> | А значит, по условию различимости для <tex> q_1 </tex> и <tex> q_2</tex> , <tex> t_1 \in T \Leftrightarrow t_2 \notin T </tex> | ||
}} | }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | === Пример === | |
| − | + | [[Файл:avtomat2.png|200px]] [[Файл:avtomat3.png|200px]] | |
| − | + | ||
| + | Эти два автомата принимают слова из языка слов длины не меньше одного, состоящих из символов алфавита <tex> \lbrace 0, 1\rbrace </tex>. Стартовые и все допускающие состояния автоматов эквивалентны между собой. | ||
| + | |||
| + | [[Категория: Теория формальных языков]] | ||
| + | [[Категория: Автоматы и регулярные языки]] | ||
| + | |||
| + | == Проверка ДКА на эквивалентность == | ||
| + | Заданы два автомата: <tex> \mathcal{A}_1 </tex> со стартовым состоянием <tex> s_1 </tex> и <tex> \mathcal{A}_2 </tex> со стартовым состоянием <tex> s_2 </tex> соответственно. Нужно проверить их на эквивалентность. | ||
| − | + | '''Замечание:''' для реализации оба автомата обязательно должны иметь [[Детерминированные_конечные_автоматы#допускает|дьявольские состояния]]. | |
| − | + | === Проверка через минимизацию === | |
| − | + | Для этого построим автомат <tex> \mathcal{A} </tex>, содержащий все состояния обоих автоматов и изначальные переходы между ними. Стартовым состоянием в новом автомате можно сделать <tex> s_1 </tex> или <tex> s_2 </tex> — это не имеет значения. При этом состояния одного из автоматов станут недостижимыми из новой стартовой вершины в новом автомате, но для алгоритма это и не важно.<br> | |
| + | [[Файл:auto_equiq.png|470px]]<br> | ||
| + | Осталось лишь проверить на эквивалентность состояния <tex> s_1 </tex> и <tex> s_2 </tex> в полученном автомате. Их эквивалентность совпадает с эквивалентностью автоматов <tex> \mathcal{A}_1 </tex> и <tex> \mathcal{A}_2 </tex>. Для этого можно применить [[Минимизация_ДКА,_алгоритм_за_O(n%5E2)_с_построением_пар_различимых_состояний|алгоритм минимизации ДКА]], который разбивает все состояния на классы эквивалентности. Если состояния <tex>s_1</tex> и <tex>s_2</tex> нового автомата в одном классе эквивалентности {{---}} исходные автоматы эквивалентны. | ||
| − | + | Также можно минимизировать каждый автомат отдельно и проверить минимизированные версии на изоморфизм. | |
| − | + | === Проверка через BFS === | |
| − | + | Два автомата можно также проверить на эквивалентность, используя [[Обход в ширину | обход в ширину]]. Будем синхронно обходить два автомата, начиная со стартовых состояний, в поисках такой строки, которая различает два состояния этих автоматов. То есть она будет допускаться одним автоматом, но не будет принадлежать языку другого. | |
| − | + | Поскольку эквивалентные автоматы допускают один и тот же язык, при переходе по одним и тем же символам в обоих автоматах, слово должно приниматься обоими автоматами одновременно. То есть вершины, в которые мы перешли, должны быть либо одновременно терминальными, либо одновременно нетерминальными, что и проверяет приведённый алгоритм. | |
| + | ==== Псевдокод ==== | ||
| + | <font color=green>// $\mathtt{aut}[i][c]$ {{---}} номер состояния, в которое есть переход из состояния $i$ по символу $c$</font> | ||
| + | '''boolean''' $\mathtt{bfsEquivalenceCheck}$($\mathtt{aut1}$ : '''int[][]''', $\mathtt{aut2}$ : '''int[][]'''): | ||
| + | $Q.\mathtt{push}(\langle s_1, s_2 \rangle) $ <font color=green>// <tex> Q </tex> {{---}} очередь из пар состояний</font> | ||
| + | '''while''' $Q \ne \varnothing $ | ||
| + | $u, v \leftarrow Q.\mathtt{pop}()$ | ||
| + | '''if''' $\mathtt{isTerminal1[u]} \ne \mathtt{isTerminal2[v]}$ | ||
| + | '''return''' ''false'' | ||
| + | $\mathtt{used[u][v]} \leftarrow $ ''true'' | ||
| + | '''for''' $c \in \Sigma$ | ||
| + | '''if''' '''not''' $\mathtt{used[aut1[u][c]][aut2[v][c]]}$ | ||
| + | $Q.\mathtt{push}(\langle \mathtt{aut1}[u][c], \mathtt{aut2}[v][c] \rangle)$ | ||
| + | '''return''' ''true'' | ||
| − | + | Корректность алгоритма следует из строго доказательства того факта, что если два состояния $u$ и $v$ различаются какой-то строкой, то они различаются строкой длины $O(n)$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Алгоритм | + | Интуитивное понимание алгоритма такое: пусть по строке $w$ мы пришли в состояния $ \langle u, v \rangle $, и пусть они оба нетерминальные. После этого совершим переход по символу $c$ в состояния $ \langle u', v' \rangle $. |
| − | [ | + | |
| + | Тогда если $\mathtt{isTerminal1[u']} \ne \mathtt{isTerminal2[v']}$, то строка $wc$ различает эти два состояния. А значит автоматы не эквивалентны. | ||
| + | |||
| + | == См. также == | ||
| + | * [[Минимизация_ДКА,_алгоритм_за_O(n%5E2)_с_построением_пар_различимых_состояний|Алгоритм минимизации ДКА]] | ||
| + | * [[Минимизация ДКА, алгоритм Хопкрофта (сложность O(n log n))]] | ||
| + | |||
| + | == Источники информации == | ||
| + | * [http://stackoverflow.com/questions/6905043/equivalence-between-two-automata/12623361#12623361 StackOverflow {{---}} Equivalence between two automata] | ||
Текущая версия на 19:33, 4 сентября 2022
Связь эквивалентности состояний и различимости состояний
| Определение: |
| Два автомата и называются эквивалентными (англ. equivalent), если они распознают один и тот же язык над алфавитом , то есть . |
| Определение: |
Слово различает (англ. distinguish) два состояния и , если
|
| Определение: |
Два состояния и называются эквивалентными , если не существует строки, которая их различает, то есть верно, что
|
Заметим, что эквивалентность состояний действительно является отношением эквивалентности. Так как (равносильность) является отношением эквивалентности и в детерминированном автомате всегда существует путь по любому слову, описанное нами отношение является отношением эквивалентности.
| Лемма: |
, , , различает и . Тогда различает и . |
| Доказательство: |
|
А значит, по условию различимости для и , |
Пример
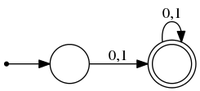
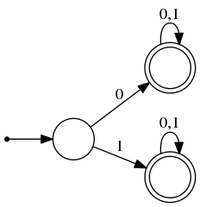
Эти два автомата принимают слова из языка слов длины не меньше одного, состоящих из символов алфавита . Стартовые и все допускающие состояния автоматов эквивалентны между собой.
Проверка ДКА на эквивалентность
Заданы два автомата: со стартовым состоянием и со стартовым состоянием соответственно. Нужно проверить их на эквивалентность.
Замечание: для реализации оба автомата обязательно должны иметь дьявольские состояния.
Проверка через минимизацию
Для этого построим автомат , содержащий все состояния обоих автоматов и изначальные переходы между ними. Стартовым состоянием в новом автомате можно сделать или — это не имеет значения. При этом состояния одного из автоматов станут недостижимыми из новой стартовой вершины в новом автомате, но для алгоритма это и не важно.
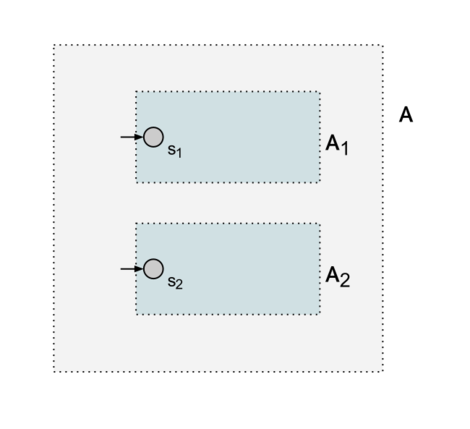
Осталось лишь проверить на эквивалентность состояния и в полученном автомате. Их эквивалентность совпадает с эквивалентностью автоматов и . Для этого можно применить алгоритм минимизации ДКА, который разбивает все состояния на классы эквивалентности. Если состояния и нового автомата в одном классе эквивалентности — исходные автоматы эквивалентны.
Также можно минимизировать каждый автомат отдельно и проверить минимизированные версии на изоморфизм.
Проверка через BFS
Два автомата можно также проверить на эквивалентность, используя обход в ширину. Будем синхронно обходить два автомата, начиная со стартовых состояний, в поисках такой строки, которая различает два состояния этих автоматов. То есть она будет допускаться одним автоматом, но не будет принадлежать языку другого.
Поскольку эквивалентные автоматы допускают один и тот же язык, при переходе по одним и тем же символам в обоих автоматах, слово должно приниматься обоими автоматами одновременно. То есть вершины, в которые мы перешли, должны быть либо одновременно терминальными, либо одновременно нетерминальными, что и проверяет приведённый алгоритм.
Псевдокод
// $\mathtt{aut}[i][c]$ — номер состояния, в которое есть переход из состояния $i$ по символу $c$
boolean $\mathtt{bfsEquivalenceCheck}$($\mathtt{aut1}$ : int[][], $\mathtt{aut2}$ : int[][]):
$Q.\mathtt{push}(\langle s_1, s_2 \rangle) $ // — очередь из пар состояний
while $Q \ne \varnothing $
$u, v \leftarrow Q.\mathtt{pop}()$
if $\mathtt{isTerminal1[u]} \ne \mathtt{isTerminal2[v]}$
return false
$\mathtt{used[u][v]} \leftarrow $ true
for $c \in \Sigma$
if not $\mathtt{used[aut1[u][c]][aut2[v][c]]}$
$Q.\mathtt{push}(\langle \mathtt{aut1}[u][c], \mathtt{aut2}[v][c] \rangle)$
return true
Корректность алгоритма следует из строго доказательства того факта, что если два состояния $u$ и $v$ различаются какой-то строкой, то они различаются строкой длины $O(n)$.
Интуитивное понимание алгоритма такое: пусть по строке $w$ мы пришли в состояния $ \langle u, v \rangle $, и пусть они оба нетерминальные. После этого совершим переход по символу $c$ в состояния $ \langle u', v' \rangle $.
Тогда если $\mathtt{isTerminal1[u']} \ne \mathtt{isTerminal2[v']}$, то строка $wc$ различает эти два состояния. А значит автоматы не эквивалентны.