Детерминированные автоматы с магазинной памятью — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
м
м (rollbackEdits.php mass rollback)
 
(не показано 15 промежуточных версий 8 участников)
Строка 1: Строка 1:
 
{{Определение
 
{{Определение
 
|definition =
 
|definition =
−
<b> Автоматом с магазинной памятью </b> называется набор <tex> A = \langle\Sigma,Q,s\in Q, \Gamma,  Z_0 \in \Gamma, T \subset Q, \delta : Q \times \Sigma \cup \{\varepsilon\} \times \Gamma \rightarrow \cal P</tex><tex>(Q \times \Gamma^*)\rangle </tex>, где <br>
+
'''Детерминированным автоматом с магазинной памятью''' (англ. ''deterministic pushdown automaton'') называется [[Автоматы с магазинной памятью|автомат с магазинной памятью]], для которого выполнены следующие условия:
−
* <tex>\Sigma</tex>: конечное множество входных символов.
 
−
* <tex>Q</tex>: конечное множество состояний.
 
−
* <tex>s</tex>: начальное состояние.
 
−
* <tex>\Gamma</tex>: конечный магазинный алфавит {{---}} множество символов, которые можно помещать в магазин.
 
−
* <tex>Z_0</tex>: начальный магазинный символ (маркер дна). Находится в магазине в начале работы автомата.
 
−
* <tex>T</tex>: множество допускающих состояний.
 
−
* <tex>\delta</tex>: функция переходов. <tex>\delta (q,a,X)=(p,\gamma)</tex>, где
 
−
** <tex>q</tex>: текущее состояние из Q.
 
−
** <tex>a</tex>: входной символ или <tex>\epsilon</tex>.
 
−
** <tex>X</tex>: магазинный символ из <tex>\Gamma</tex>.
 
−
** <tex>p</tex>: новое состояние из Q.
 
−
** <tex>\gamma</tex>: цепочка магазинных символов, <i>замещающих</i> <tex>X</tex> на вершине магазина.
 
−
}}
 
−
{{Определение
 
−
|definition =
 
−
<b>Детерменированным автоматом с магазинной памятью</b> называется автомат с магазинной памятью, для которого выполнены следующие условия:
 
 
#<tex>\mathcal8 q \in Q, a \in \Sigma \cup \{ \varepsilon \}, X \in \Gamma \Rightarrow \delta(q, a, X)</tex> имеет не более одного элемента {{---}} <tex> \delta : Q \times \Sigma \cup \{\varepsilon\} \times \Gamma \rightarrow Q \times \Gamma^*</tex>.
 
#<tex>\mathcal8 q \in Q, a \in \Sigma \cup \{ \varepsilon \}, X \in \Gamma \Rightarrow \delta(q, a, X)</tex> имеет не более одного элемента {{---}} <tex> \delta : Q \times \Sigma \cup \{\varepsilon\} \times \Gamma \rightarrow Q \times \Gamma^*</tex>.
−
#Если <tex>\delta (q,a,X)</tex> непусто для некоторого <tex>a \in \Sigma</tex>, то <tex>\delta (q,\epsilon,X)</tex> должно быть пустым.
+
#Если <tex>\delta (q,a,X)</tex> непусто для некоторого <tex>a \in \Sigma</tex>, то <tex>\delta (q,\varepsilon,X)</tex> должно быть пустым.
 
}}
 
}}
−
Будем обозначать переход автомата из состояния <tex>(q_1,a_1,X_1)</tex> в состояние <tex>(q_2,a_2,X_2)</tex> как <tex>(q_1,a_1,X_1)\vdash(q_2,a_2,X_2)</tex>. Переход автомата из состояния <tex>(q_1,a_1,X_1)</tex> в состояние <tex>(q_{p+1},a_{p+1},X_{p+1})</tex> через <tex>P</tex> промежуточных состояний обозначаем <tex>(q_1,a_1,X_1)\vdash^*_P(q_{p+1},a_{p+1},X_{p+1})</tex>.
 
  
 
==Пример==
 
==Пример==
−
Автомат <tex>A=(\{0,1\},\{q,p\},q, \{Z_0,X\}, Z_0,\{p\}, \delta)</tex> с функией перехода <tex>\delta</tex>:
+
Построим для языка:
 +
# <tex> S \rightarrow 1H </tex>
 +
# <tex> H \rightarrow 0F </tex>
 +
# <tex> H \rightarrow \varepsilon </tex>
 +
# <tex> F \rightarrow 0F </tex>
 +
# <tex> F \rightarrow 1F </tex>
 +
# <tex> F \rightarrow \varepsilon </tex>
 +
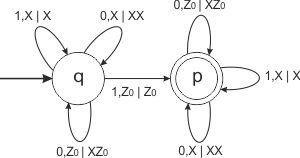
автомат <tex>A=(\{0,1\}, \{Z_0,X\}, \{q,p\}, q, \{p\}, Z_0, \delta)</tex> с функией перехода <tex>\delta</tex>:
 
# <tex>\delta(q,0,Z_0)=(q,XZ_0)</tex>
 
# <tex>\delta(q,0,Z_0)=(q,XZ_0)</tex>
−
# <tex>\delta(q,0,X)=(q,XX)</tex>
+
# <tex>\delta(q,0,X) =(q,XX)</tex>
−
# <tex>\delta(q,1,X)=(q,X)</tex>
+
# <tex>\delta(q,1,X) =(q,X)</tex>
 
# <tex>\delta(q,1,Z_0)=(p,Z_0)</tex>
 
# <tex>\delta(q,1,Z_0)=(p,Z_0)</tex>
 
# <tex>\delta(p,0,Z_0)=(p,XZ_0)</tex>
 
# <tex>\delta(p,0,Z_0)=(p,XZ_0)</tex>
−
# <tex>\delta(p,0,X)=(p,XX)</tex>
+
# <tex>\delta(p,0,X) =(p,XX)</tex>
−
# <tex>\delta(p,1,X)=(p,X)</tex> <br> <br>
+
# <tex>\delta(p,1,X) =(p,X)</tex> <br> <br>
 
[[Файл:Пример_мп-автомата.png]]
 
[[Файл:Пример_мп-автомата.png]]
 +
 +
== См. также ==
 +
* [[Детерминированные автоматы с магазинной памятью, допуск по пустому стеку]]
 +
* [[Несовпадение класса языков, распознаваемых ДМП автоматами и произвольными МП автоматами]]
 +
* [[ДМП-автоматы и неоднозначность]]
 +
 +
== Источники информации ==
 +
* ''Хопкрофт Д., Мотвани Р., Ульман Д.'' {{---}} '''Введение в теорию автоматов, языков и вычислений''', 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2008. — 528с. : ISBN 978-5-8459-1347-0 (рус.)
 +
 +
[[Категория: Теория формальных языков]]
 +
[[Категория: Контекстно-свободные грамматики]]
 +
[[Категория: МП-автоматы]]

Текущая версия на 19:39, 4 сентября 2022

Определение:
Детерминированным автоматом с магазинной памятью (англ. deterministic pushdown automaton) называется автомат с магазинной памятью, для которого выполнены следующие условия:
  1. [math]\mathcal8 q \in Q, a \in \Sigma \cup \{ \varepsilon \}, X \in \Gamma \Rightarrow \delta(q, a, X)[/math] имеет не более одного элемента — [math] \delta : Q \times \Sigma \cup \{\varepsilon\} \times \Gamma \rightarrow Q \times \Gamma^*[/math].
  2. Если [math]\delta (q,a,X)[/math] непусто для некоторого [math]a \in \Sigma[/math], то [math]\delta (q,\varepsilon,X)[/math] должно быть пустым.


Пример

Построим для языка:

  1. [math] S \rightarrow 1H [/math]
  2. [math] H \rightarrow 0F [/math]
  3. [math] H \rightarrow \varepsilon [/math]
  4. [math] F \rightarrow 0F [/math]
  5. [math] F \rightarrow 1F [/math]
  6. [math] F \rightarrow \varepsilon [/math]

автомат [math]A=(\{0,1\}, \{Z_0,X\}, \{q,p\}, q, \{p\}, Z_0, \delta)[/math] с функией перехода [math]\delta[/math]:

  1. [math]\delta(q,0,Z_0)=(q,XZ_0)[/math]
  2. [math]\delta(q,0,X) =(q,XX)[/math]
  3. [math]\delta(q,1,X) =(q,X)[/math]
  4. [math]\delta(q,1,Z_0)=(p,Z_0)[/math]
  5. [math]\delta(p,0,Z_0)=(p,XZ_0)[/math]
  6. [math]\delta(p,0,X) =(p,XX)[/math]
  7. [math]\delta(p,1,X) =(p,X)[/math]

Пример мп-автомата.png

См. также

Источники информации

  • Хопкрофт Д., Мотвани Р., Ульман Д. — Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2008. — 528с. : ISBN 978-5-8459-1347-0 (рус.)
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Детерминированные_автоматы_с_магазинной_памятью&oldid=85729»