Алгоритм Прима — различия между версиями
(→Идея) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 97 промежуточных версий 12 участников) | |||
| Строка 1: | Строка 1: | ||
| − | Алгоритм Прима — алгоритм поиска [[Лемма о безопасном ребре#Минимальное остовное дерево|минимального остовного дерева]] (minimum spanning tree, MST) во взвешенном неориентированном связном графе. | + | '''Алгоритм Прима''' (англ. ''Prim's algorithm'') — алгоритм поиска [[Лемма о безопасном ребре#Минимальное остовное дерево|минимального остовного дерева]] (англ. ''minimum spanning tree, MST'') во взвешенном [[Основные определения теории графов#Неориентированные графы | неориентированном связном графе]]. |
== Идея == | == Идея == | ||
| − | Данный алгоритм очень похож на [[алгоритм Дейкстры]]. Будем последовательно строить поддерево <tex>F</tex> ответа в графе <tex>G</tex>, поддерживая приоритетную очередь <tex>Q</tex> из вершин <tex>G \setminus F</tex>, | + | Данный алгоритм очень похож на [[алгоритм Дейкстры]]. Будем последовательно строить поддерево <tex>F</tex> ответа в графе <tex>G</tex>, поддерживая [[Дискретная_математика,_алгоритмы_и_структуры_данных#.D0.9F.D1.80.D0.B8.D0.BE.D1.80.D0.B8.D1.82.D0.B5.D1.82.D0.BD.D1.8B.D0.B5_.D0.BE.D1.87.D0.B5.D1.80.D0.B5.D0.B4.D0.B8 | приоритетную очередь]] <tex>Q</tex> из вершин <tex>G \setminus F</tex>, в которой ключом для вершины <tex>v</tex> является <tex>\min\limits_{u \in V(F), uv \in E(G)}w(uv)</tex> — вес минимального ребра из вершин <tex>F</tex> в вершины <tex>G \setminus F</tex>. Также для каждой вершины в очереди будем хранить <tex>p(v)</tex> — вершину <tex>u</tex>, на которой достигается минимум в определении ключа. Дерево <tex>F</tex> поддерживается неявно, и его ребра — это пары <tex>\left(v,p(v)\right)</tex>, где <tex>v \in G \setminus \{r\} \setminus Q</tex>, а <tex>r</tex> — корень <tex>F</tex>. Изначально <tex>F</tex> пусто и значения ключей у всех вершин равны <tex>+\infty</tex>. Выберём произвольную вершину <tex>r</tex> и присвоим её ключу значение <tex>0</tex>. На каждом шаге будем извлекать минимальную вершину <tex>v</tex> из приоритетной очереди и релаксировать все ребра <tex>vu</tex>, такие что <tex>u \in Q</tex>, выполняя при этом операцию <tex>\text{decreaseKey}</tex> над очередью и обновление <tex>p(v)</tex>. Ребро <tex>\left(v,p(v)\right)</tex> при этом добавляется к ответу. |
| + | == Реализация == | ||
| + | <font color=green>// <tex>G</tex> {{---}} исходный граф</font> | ||
| + | <font color=green>// <tex>w</tex> {{---}} весовая функция</font> | ||
| + | '''function''' <tex>\mathtt{primFindMST}():</tex> | ||
| + | '''for''' <tex>v \in V(G)</tex> | ||
| + | <tex>\mathtt{key}[v]\ =\ \infty</tex> | ||
| + | <tex>\mathtt{p}[v]\ =</tex> ''null'' | ||
| + | <tex>r\ =</tex> произвольная вершина графа <tex>G</tex> | ||
| + | <tex>\mathtt{key}[r]\ =\ \mathtt{0}</tex> | ||
| + | <tex>Q.\mathtt{push}(V(G))</tex> | ||
| + | '''while not''' <tex>Q.\mathtt{isEmpty()}</tex> | ||
| + | <tex>v\ =\ Q.\mathtt{extractMin}()</tex> | ||
| + | '''for''' <tex>vu \in E(G)</tex> | ||
| + | '''if''' <tex>u \in Q</tex> '''and''' <tex>\mathtt{key}[u] > w(v, u)</tex> | ||
| + | <tex>\mathtt{p}[u]\ =\ v</tex> | ||
| + | <tex>\mathtt{key}[u]\ =\ w(v, u)</tex> | ||
| + | <tex>Q.\mathtt{decreaseKey}(u, \mathtt{key}[u])</tex> | ||
| − | + | Ребра дерева восстанавливаются из его неявного вида после выполнения алгоритма.<br> | |
| − | + | Чтобы упростить операцию <tex>\mathrm{decreaseKey}</tex> можно написать кучу на основе [[АВЛ-дерево | сбалансированного бинарного дерева поиска]]. Тогда просто удалим вершину и добавим ее обратно уже с новым ключом. Асимптотика таких преобразований <tex>O(\log n)</tex>. Если же делать с [[Двоичная_куча | бинарной кучей]], то вместо операции <tex>\mathrm{decreaseKey}</tex>, будем всегда просто добавлять вершину с новым ключом, если из кучи достали вершину с ключом, значение которого больше чем у нее уже стоит, просто игнорировать. Вершин в куче будет не больше <tex>n^2</tex>, следовательно, операция <tex>\mathrm{extractMin}</tex> будет выполняться за <tex>O(\log n^2)</tex>, что равно <tex>O(\log n)</tex>. Максимальное количество вершин, которое мы сможем достать, равняется количеству ребер, то есть <tex>m</tex>, поэтому общая асимптотика составит <tex>O(m \log n)</tex>, что хорошо только на разреженных графах. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ==Пример== | ||
| + | Рассмотрим работу алгоритма на примере графа. | ||
| + | Пусть произвольно выбранная вершина — это вершина a. | ||
| + | {| cellpadding = "20" class = "wikitable" | ||
| + | ! Изображение !! Множество вершин !! Описание | ||
| + | |- | ||
| + | |[[Файл:Mst_prima_1.png|200px]] | ||
| + | | | ||
| + | {| width="100%" style = "text-align: center" | ||
| + | | '''a''' || '''b''' || '''c''' || '''d''' || '''e''' | ||
| + | |- | ||
| + | | <tex> 0 </tex> || <tex>\infty</tex> || <tex>\infty</tex> || <tex>\infty</tex> || <tex>\infty</tex> | ||
| + | |} | ||
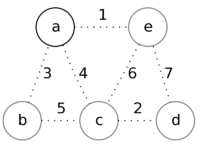
| + | |style="padding-left: 1em" | Извлечём из множества вершину '''a''', так как её приоритет минимален.<br/>Рассмотрим смежные с ней вершины '''b''', '''c''', и '''e'''. <br/>Обновим их приоритеты, как веса соответствующих рёбер '''ab''', '''ac''' и '''ae''', которые будут добавлены в ответ. | ||
| + | |- | ||
| + | |[[Файл:Mst_prima_2.png|200px]] | ||
| + | | | ||
| + | {| width="100%" style = "text-align: center" | ||
| + | | a || '''b''' || '''c''' || '''d''' || '''e''' | ||
| + | |- | ||
| + | | <tex> 0 </tex> || <tex> 3 </tex> || <tex> 4 </tex> || <tex>\infty</tex> || <tex> 1 </tex> | ||
| + | |} | ||
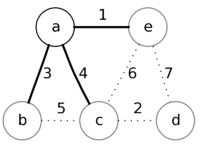
| + | |style="padding-left: 1em" |Теперь минимальный приоритет у вершины '''е'''.<br/> Извлечём её и рассмотрим смежные с ней вершины '''a''', '''c''', и '''d'''.<br/>Изменим приоритет только у вершины '''d''', так как приоритеты вершин '''a''' и '''с''' меньше,<br/>чем веса у соответствующих рёбер '''ea''' и '''ec''', и установим приоритет вершины '''d''' равный весу ребра '''ed''', которое будет добавлено в ответ. | ||
| + | |- | ||
| + | |[[Файл:Mst_prima_3.png|200px]] | ||
| + | | | ||
| + | {| width="100%" style = "text-align: center" | ||
| + | | a || '''b''' || '''c''' || '''d''' || e | ||
| + | |- | ||
| + | | <tex> 0 </tex> || <tex> 3 </tex> || <tex> 4 </tex> || <tex> 7 </tex> || <tex> 1 </tex> | ||
| + | |} | ||
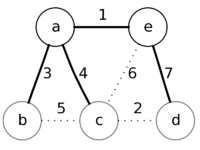
| + | |style="padding-left: 1em" |После извлечения вершины '''b''' ничего не изменится, так как приоритеты вершин '''a''' и '''с''' меньше,<br/>чем веса у соответствующих рёбер '''ba''' и '''bc'''. Однако, после извлечения следующей вершины {{---}} '''c''',<br/>будет обновлён приоритет у вершины '''d''' на более низкий (равный весу ребра '''cd''') и в ответе ребро '''ed''' будет заменено на '''cd'''. | ||
| + | |- | ||
| + | |[[Файл:Mst_prima_4.png|200px]] | ||
| + | | | ||
| + | {| width="100%" style = "text-align: center" | ||
| + | | a || b || c || '''d''' || e | ||
| + | |- | ||
| + | | <tex> 0 </tex> || <tex> 3 </tex> || <tex> 4 </tex> || <tex> 2 </tex> || <tex> 1 </tex> | ||
| + | |} | ||
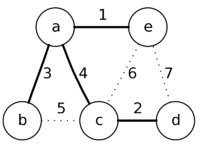
| + | |style="padding-left: 1em" |Далее будет рассмотрена следующая вершина {{---}} '''d''', но ничего не изменится,<br/>так как приоритеты вершин '''e''' и '''с''' меньше, чем веса у соответствующих рёбер '''de''' и '''dc'''.<br/>После этого алгоритм завершит работу, так как в заданном множестве не останется вершин,<br/>которые не были бы рассмотрены | ||
| + | |} | ||
== Корректность == | == Корректность == | ||
| − | По поддерживаемым инвариантам после извлечения вершины <tex>v | + | По поддерживаемым инвариантам после извлечения вершины <tex>v\ (v \neq r)</tex> из <tex>Q</tex> ребро <tex>\left(v,p(v)\right)</tex> является ребром минимального веса, пересекающим разрез <tex>\left(F,Q\right)</tex>. Значит, по [[Лемма о безопасном ребре|лемме о безопасном ребре]], оно безопасно. Алгоритм построения ''MST'', добавляющий безопасные ребра, причём делающий это ровно <tex>|V|-1</tex> раз, корректен. |
== Оценка производительности == | == Оценка производительности == | ||
| − | Производительность алгоритма Прима зависит от выбранной реализации приоритетной очереди, как и в | + | Производительность алгоритма Прима зависит от выбранной реализации приоритетной очереди, как и в алгоритме Дейкстры. Извлечение минимума выполняется <tex>V</tex> раз, релаксация — <tex>O(E)</tex> раз. |
{| border="1" cellpadding="5" cellspacing="0" style="text-align:center" width=30% | {| border="1" cellpadding="5" cellspacing="0" style="text-align:center" width=30% | ||
| Строка 43: | Строка 81: | ||
|style="background:#f9f9f9"|<tex>O(V^2+E)</tex> | |style="background:#f9f9f9"|<tex>O(V^2+E)</tex> | ||
|- | |- | ||
| − | |style="background:#f9f9f9"|Двоичная куча | + | |style="background:#f9f9f9"|[[Двоичная куча]] |
|style="background:#f9f9f9"|<tex>O(E\log{V})</tex> | |style="background:#f9f9f9"|<tex>O(E\log{V})</tex> | ||
|- | |- | ||
| − | |style="background:#f9f9f9"| | + | |style="background:#f9f9f9"|[[Фибоначчиевы кучи|Фибоначчиева куча]] |
|style="background:#f9f9f9"|<tex>O(V\log{V}+E)</tex> | |style="background:#f9f9f9"|<tex>O(V\log{V}+E)</tex> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | == См. также == | + | ==См. также== |
* [[Алгоритм Краскала]] | * [[Алгоритм Краскала]] | ||
| + | * [[Алгоритм Борувки]] | ||
| − | == | + | == Источники информации == |
| − | * | + | *Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн — Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — с.653 — 656.— ISBN 978-5-8459-0857-5 (рус.) |
| + | *[http://ru.wikipedia.org/wiki/%D0%90%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC_%D0%9F%D1%80%D0%B8%D0%BC%D0%B0 Википедия — Алгоритм Прима] | ||
| + | *[http://en.wikipedia.org/wiki/Prim%27s_algorithm Wikipedia — Prim's algorithm] | ||
| + | *[http://e-maxx.ru/algo/mst_prim MAXimal :: algo :: Минимальное остовное дерево. Алгоритм Прима] | ||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Остовные деревья ]] | [[Категория: Остовные деревья ]] | ||
| + | [[Категория: Построение остовных деревьев]] | ||
Текущая версия на 19:12, 4 сентября 2022
Алгоритм Прима (англ. Prim's algorithm) — алгоритм поиска минимального остовного дерева (англ. minimum spanning tree, MST) во взвешенном неориентированном связном графе.
Идея
Данный алгоритм очень похож на алгоритм Дейкстры. Будем последовательно строить поддерево ответа в графе , поддерживая приоритетную очередь из вершин , в которой ключом для вершины является — вес минимального ребра из вершин в вершины . Также для каждой вершины в очереди будем хранить — вершину , на которой достигается минимум в определении ключа. Дерево поддерживается неявно, и его ребра — это пары , где , а — корень . Изначально пусто и значения ключей у всех вершин равны . Выберём произвольную вершину и присвоим её ключу значение . На каждом шаге будем извлекать минимальную вершину из приоритетной очереди и релаксировать все ребра , такие что , выполняя при этом операцию над очередью и обновление . Ребро при этом добавляется к ответу.
Реализация
// — исходный граф // — весовая функция function for null произвольная вершина графа while not for if and
Ребра дерева восстанавливаются из его неявного вида после выполнения алгоритма.
Чтобы упростить операцию можно написать кучу на основе сбалансированного бинарного дерева поиска. Тогда просто удалим вершину и добавим ее обратно уже с новым ключом. Асимптотика таких преобразований . Если же делать с бинарной кучей, то вместо операции , будем всегда просто добавлять вершину с новым ключом, если из кучи достали вершину с ключом, значение которого больше чем у нее уже стоит, просто игнорировать. Вершин в куче будет не больше , следовательно, операция будет выполняться за , что равно . Максимальное количество вершин, которое мы сможем достать, равняется количеству ребер, то есть , поэтому общая асимптотика составит , что хорошо только на разреженных графах.
Пример
Рассмотрим работу алгоритма на примере графа. Пусть произвольно выбранная вершина — это вершина a.
Корректность
По поддерживаемым инвариантам после извлечения вершины из ребро является ребром минимального веса, пересекающим разрез . Значит, по лемме о безопасном ребре, оно безопасно. Алгоритм построения MST, добавляющий безопасные ребра, причём делающий это ровно раз, корректен.
Оценка производительности
Производительность алгоритма Прима зависит от выбранной реализации приоритетной очереди, как и в алгоритме Дейкстры. Извлечение минимума выполняется раз, релаксация — раз.
| Структура данных для приоритетной очереди | Асимптотика времени работы |
|---|---|
| Наивная реализация | |
| Двоичная куча | |
| Фибоначчиева куча |
См. также
Источники информации
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн — Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — с.653 — 656.— ISBN 978-5-8459-0857-5 (рус.)
- Википедия — Алгоритм Прима
- Wikipedia — Prim's algorithm
- MAXimal :: algo :: Минимальное остовное дерево. Алгоритм Прима